线性回归–波士顿房价
前几天,机器学习老师布置了个作业。
实验要求
- 编写一个线性回归分类器(以梯度下降更新参数;以均方误差计算cost function;补充计算accuracy的函数)
- 使用波士顿房价数据集作为实验数据集(load_boston;数据集相关信息)
- 分别使用自己编写的线性回归分类器、sklearn的线性回归分类器训练模型(sklearn的线性模型的API文档)
- 使用多项式回归优化模型
实验内容
首先,我们需要导入相关的库(由于在pycharm可以很方便的导入需要的类,所以这方面不重要)
from sklearn import preprocessing
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
1、加载数据集,划分数据,并输出训练集和测试集中数据的情况
boston = load_boston() # 加载波士顿房价数据集
print(boston.keys()) # dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])
print(boston['data'].shape,boston['target'].shape) # data为训练集,target为标签
# data的shape是(506,13),506条数据,13个特征
# target的shape是(506,)对应 506 条数据的房价
# 标准化
X = preprocessing.scale(boston['data'])
Y = preprocessing.scale(boston['target'])
data_size = Y.shape[0]
preprocessing.scale是标准化操作,默认axis=0,使得每个特征平均值为0,方差为1,源码阅读参考https://blog.csdn.net/qikaihuting/article/details/82633882
2、编写线性回归
class LinerRegression:
def __init__(self, learning_rate=0.01, max_iter=100):
# 最大迭代次数
self.max_iter = max_iter
# 学习率
self.lr = learning_rate
# 特征加上偏移量的值
self.theta = np.zeros(X.shape[1]+1)
# 13个特征对应13个权重
self.coef_ = np.zeros(X.shape[1])
# 一个偏移量,即常数项
self.intercept_ = np.zeros(1)
# 记录每次迭代的损失值
self.loss_arr = []
def fit(self, x, y):
# 如果训练集的样本数和真实值的样本数不同,则返回错误
if x.shape[0] != y.shape[0]:
raise Exception("Error! X.shape and Y.shape are incompatible")
# 每行后面加上‘1’,以便后面点乘可直接加上常数项
self.x = np.hstack([x,np.ones((len(x),1))])
self.y = y
# 开始迭代训练
for i in range(self.max_iter):
self._train_step() # 一步训练
# 记录损失值
self.loss_arr.append(self.loss())
# 更新权重
self.coef_ = self.theta[:-1]
# 更新常数项
self.intercept_ = self.theta[-1]
def _train_step(self):
# 保存权重和bias
temp = self.theta.copy()
# 我们使用批量梯度下降操作
temp = temp - self.lr * self._batch_gradient_decent(self.x , self.y)
# 得到新的权重和bias
self.theta = temp
def _batch_gradient_decent(self,x,y):
inner = x.T.dot(x.dot(self.theta.T)-y)
return inner / x.shape[0]
# 损失函数
def loss(self, y_true = None, y_predict = None):
if y_true is None or y_predict is None:
y_true = self.y
y_predict = self.x.dot(self.theta)
return np.mean((y_true - y_predict)**2)
def predict(self,x_p):
if x_p.shape[1] != len(self.coef_):
raise Exception('the feature number of X_predict must equal to X_train')
# 添加常数项
x = np.hstack([x_p,np.ones((len(x_p),1))])
# 预测并返回
return x.dot(self.theta.T)
# 计算模型得分
def score(self, y_true, y_pred):
total = sum((y_true - np.mean(y_true)) ** 2)
residual = sum((y_true - y_pred) ** 2)
R_square = 1 - residual / total
return R_square
损失函数使用的是均方差函数(常用于回归任务),参考西瓜书(2.2)
E
=
1
m
∑
i
=
1
m
(
f
(
x
i
)
?
y
i
)
2
E = \frac{1}{m}\sum_{i = 1}^{m}(f(x_i)-y_i)^2
E=m1?i=1∑m?(f(xi?)?yi?)2
梯度下降根据的公式,参考西瓜书式(3.10)
?
E
?
θ
=
2
X
T
(
X
θ
?
y
)
\frac{\partial E}{\partial \theta} = 2 X^T(X\theta - y)
?θ?E?=2XT(Xθ?y)
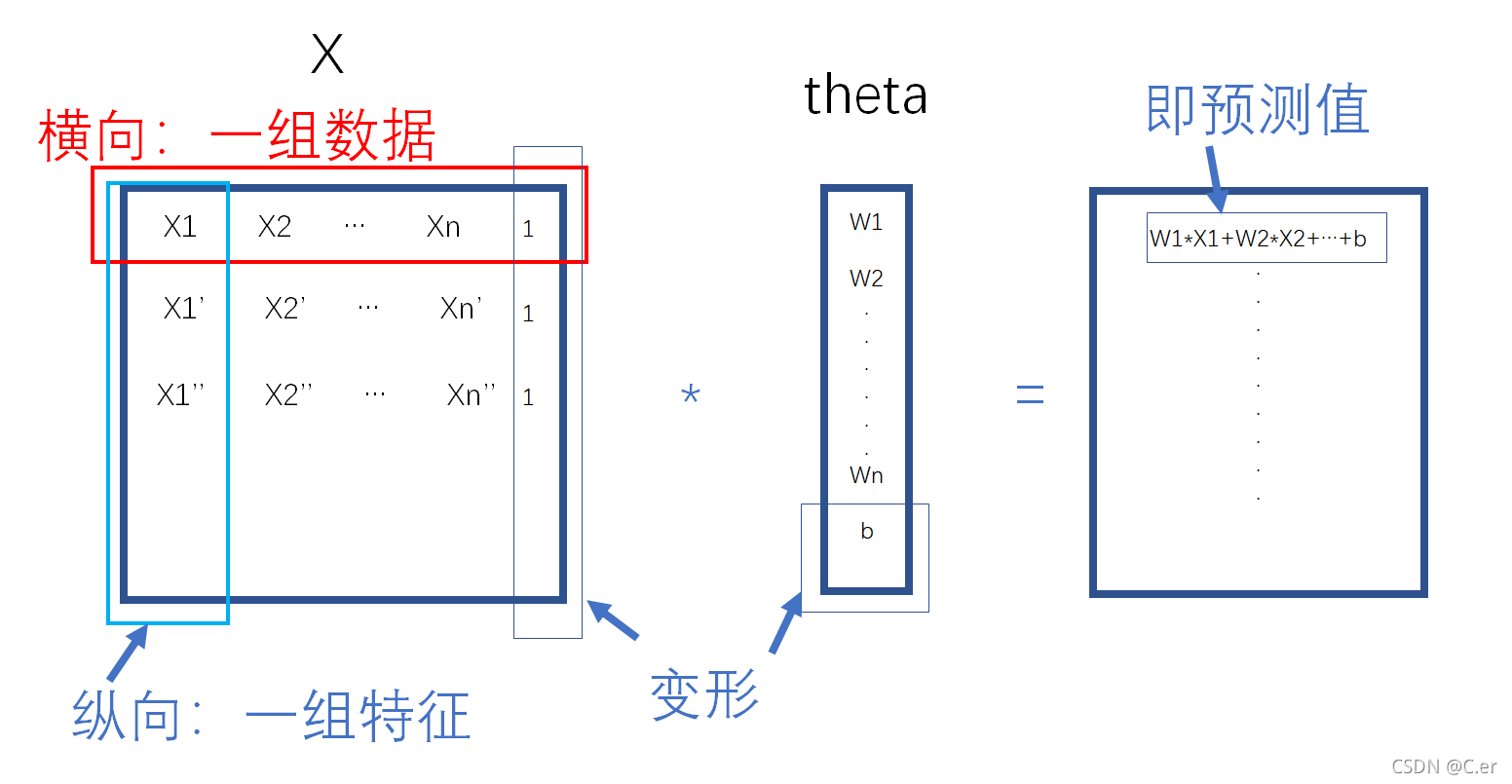
其中X和theta相乘过程如下图所示:
模型得分使用的是R^2 = 1 - RSS /TSS
其中
- ? TSS(Total Sum of Squares)表示实际值与期望值的离差平方和,代表变量的总变动程度
- ? RSS(Residual Sum of Squares)表示实际值与预测值的离差平方和,代表变量的未知变动程度
R^2取值范围在[0,1],越接近1拟合度越高
3、分别使用编写的线性回归分类器、sklearn的线性回归分类器进行模型训练,并输出在测试集的正确率,保留3位小数
# train / test split 随机排序
# 划分数据集和训练集
shuffled_index = np.random.permutation(data_size)
x = X[shuffled_index]
y = Y[shuffled_index]
split_index = int(data_size * 0.7)
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]
# 训练自己写的训练模型
regr = LinerRegression(learning_rate=0.1, max_iter=150)
regr.fit(x_train, y_train)
# 输出训练后结果
print('损失: \t{:.3}'.format(regr.loss()))
print('权重:\t' + str(regr.coef_))
print('偏移量: \t{:.3}'.format(regr.intercept_))
y_pred = regr.predict(x_train)
print('模型得分:\t{:.3}'.format(regr.score(y_train,y_pred)))
#可视化损失函数
plt.scatter(np.arange(len(regr.loss_arr)), regr.loss_arr, marker='o', c='red')
plt.show()
训练过程损失值变化如下
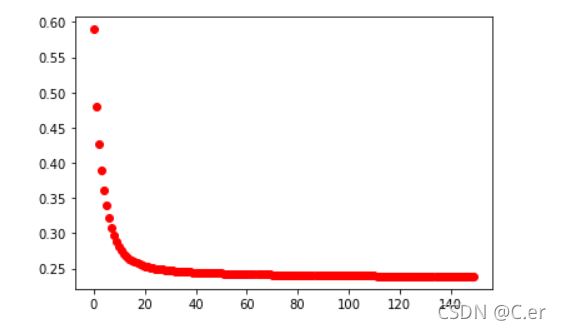
正确率为0.72
使用sklearn库进行掉包操作,其训练具体过程可以参考上面自己实现的代码
# 划分数据集和训练集,其中测试集占0.3 random_state 是 随机数种子,0或不填每次会不一样
x_train,x_test,y_train,y_test = train_test_split(boston['data'],boston['target'],test_size=0.3)
# 标准化操作,其实去掉也可以
x_train = preprocessing.scale(x_train)
x_test = preprocessing.scale(x_test)
y_train = preprocessing.scale(y_train)
y_test = preprocessing.scale(y_test)
lr = LinearRegression() # 初始化线性模型
lr.fit(x_train,y_train) # 训练模型
y_p = lr.predict(x_test) # 预测数据
print('损失:\t',lr.coef_)
print('权重:\t',lr.coef_)
print('偏移量:\t',lr.intercept_)
accuracy = lr.score(x_test,y_test)
print('模型得分:\t%.3f' %accuracy)
正确率为0.76
4、使用多项式回归进行模型优化
使用PolynomialFeatures()对训练集增加相互影响的特征
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score
# degree:控制多项式的次数;
# interaction_only:默认为 False,如果指定为 True,那么就不会有特征自己和自己结合的项,组合的特征中没有 a^2 和 b^2;
# include_bias:默认为 True 。如果为 True 的话,那么结果中就会有 0 次幂项,即全为 1 这一列。
lr = LinearRegression()
poly = PolynomialFeatures(degree=2)
# 生成相互影响的多项式的自变量
print('x_train.shape:',x_train.shape)
x_train_poly = poly.fit_transform(x_train)
print('x_train_poly.shape:',x_train_poly.shape)
lr.fit(x_train_poly, y_train)
y_p = lr.predict(x_train_poly)
print("分数为:")
print(r2_score(y_train, y_p))
此时正确值可达到0.9之多
遇到的错误
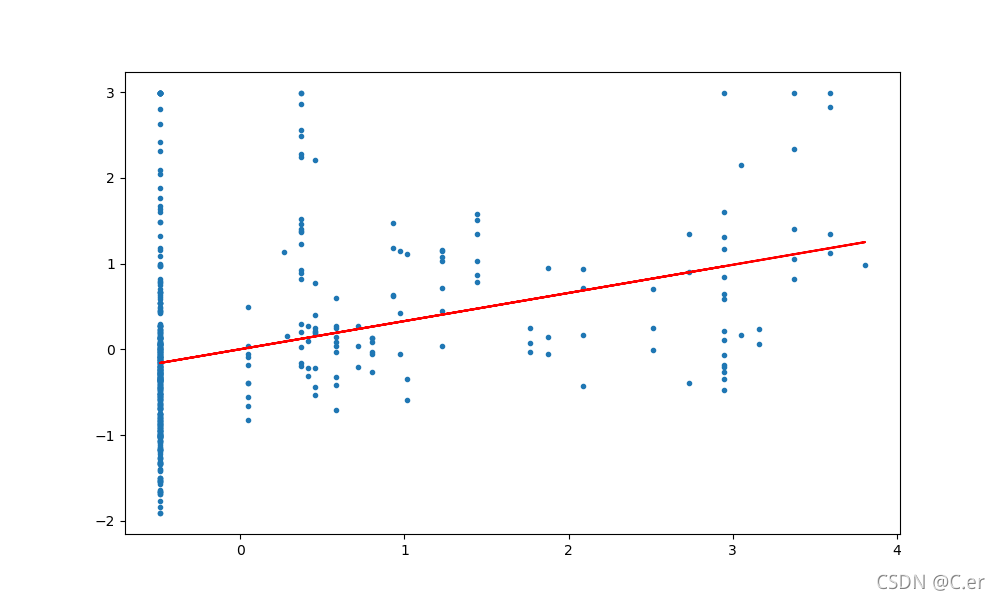
一开始拿到实验题目的时候,不管三七二十一,直接默认是简单的一元线性回归,即y=wx+b,然后把13个特征分成13份数据,每一份都和y值去单独训练,得到的结果如下:
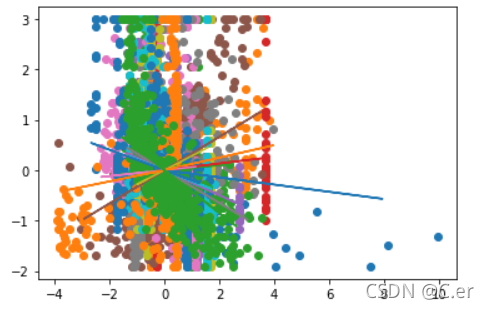
没错,一个特征表示一种颜色 (┓( ′?` )┏)
如果单独拆出来,有些数据还没那么离谱,至少看得出是个线性回归的图。
但是有些就…