文章目录
视频讲解:
【Python百日基础系列】Day05-九九乘法表 素数算法
学完前四天的内容,我说认真学习的同学已经入门了,可能同学心里还没底,因为从来没做出来一个像样的程序来,今天我们就来做几个。
一、九九乘法表
1.1 需求分析
九九乘法表是一个二维表格,需要先按行逐个计算,然后再逐行遍历,所以需要循环嵌套,行为内循环,列为外循环。
1.2 代码实现
# 九九乘法表
for i in range(1, 10):
for j in range(1, i+1):
if i*j < 10:
s_end = ' \t'
else:
s_end = '\t'
print(f'{i}x{j} = {i*j}', end=s_end)
print()
输出结果:
1x1 = 1
2x1 = 2 2x2 = 4
3x1 = 3 3x2 = 6 3x3 = 9
4x1 = 4 4x2 = 8 4x3 = 12 4x4 = 16
5x1 = 5 5x2 = 10 5x3 = 15 5x4 = 20 5x5 = 25
6x1 = 6 6x2 = 12 6x3 = 18 6x4 = 24 6x5 = 30 6x6 = 36
7x1 = 7 7x2 = 14 7x3 = 21 7x4 = 28 7x5 = 35 7x6 = 42 7x7 = 49
8x1 = 8 8x2 = 16 8x3 = 24 8x4 = 32 8x5 = 40 8x6 = 48 8x7 = 56 8x8 = 64
9x1 = 9 9x2 = 18 9x3 = 27 9x4 = 36 9x5 = 45 9x6 = 54 9x7 = 63 9x8 = 72 9x9 = 81
二、九九乘法表输出到Excel
2.1 需求分析
如果您觉得这个九九乘法表挺好,想打印出来给小孩用,怎么办呢?如果不会编程,您可能首先想到的是Excel电子表格,是吧?那么我们就把这个乘法表输出到Excel!
2.2 安装需要的包
2.2.1 进入虚拟环境
终端进入虚拟环境:py_100\scripts\activate
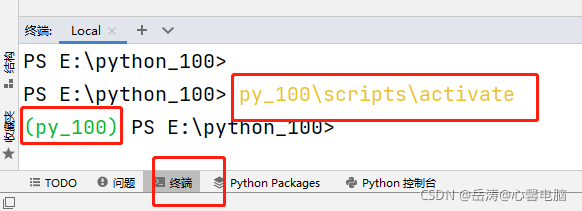
2.2.2 安装Pandas库
方法一:豆瓣源安装 pandas 和 openpyxl
pip install pandas -i https://pypi.douban.com/simple
pip install openpyxl-i https://pypi.douban.com/simple
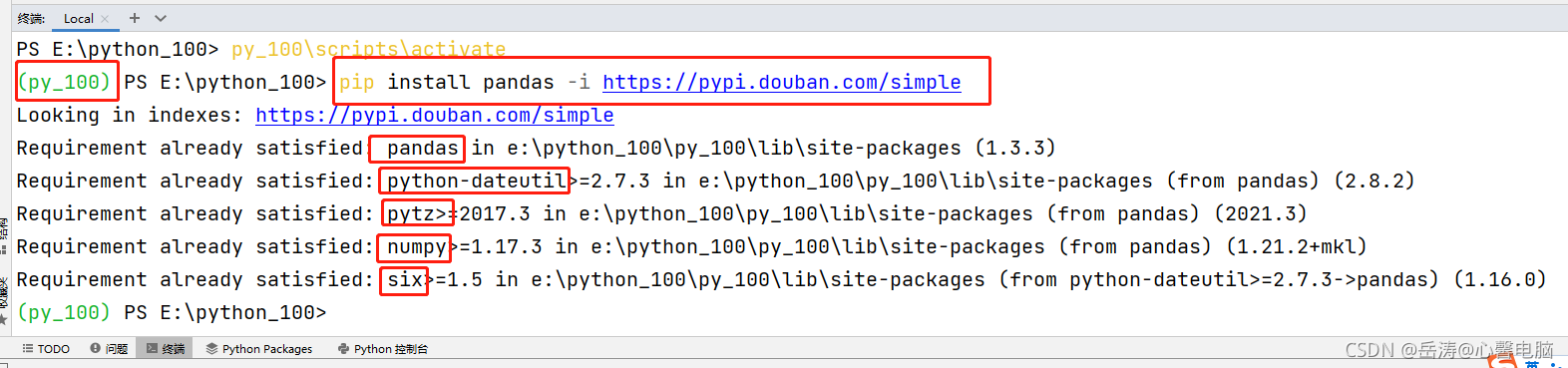
如果上述方法不成功,请使用方法二:
方法二:下载whl安装
whl下载网址之一:https://www.lfd.uci.edu/~gohlke/pythonlibs/
-
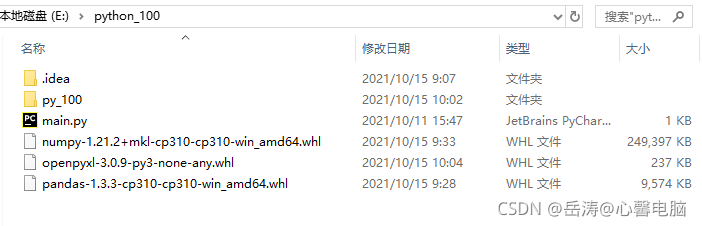
下载numpy和pandas库
https://download.lfd.uci.edu/pythonlibs/y2rycu7g/pandas-1.3.3-cp310-cp310-win_amd64.whl
https://download.lfd.uci.edu/pythonlibs/y2rycu7g/numpy-1.21.2+mkl-cp310-cp310-win_amd64.whl
https://download.lfd.uci.edu/pythonlibs/y2rycu7g/openpyxl-3.0.9-py3-none-any.whl -
复制上面三个文件到E:\python_100文件夹(根据你的需要改变)
-
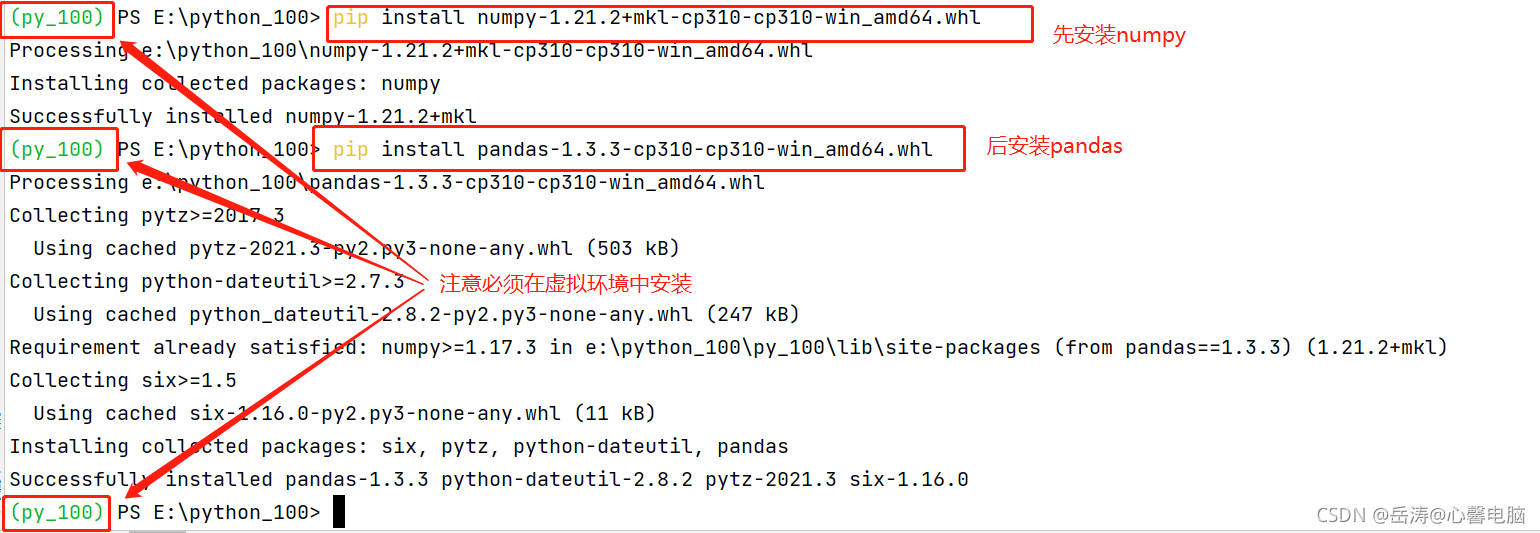
终端进入虚拟环境:
py_100\scripts\activate -
依次安装numpy、pandas 和 openpyxl:
pip install numpy-1.21.2+mkl-cp310-cp310-win_amd64.whl
pip install pandas-1.3.3-cp310-cp310-win_amd64.whl
pip install openpyxl-3.0.9-py3-none-any.whl
2.2.3 查看安装的包:pip list
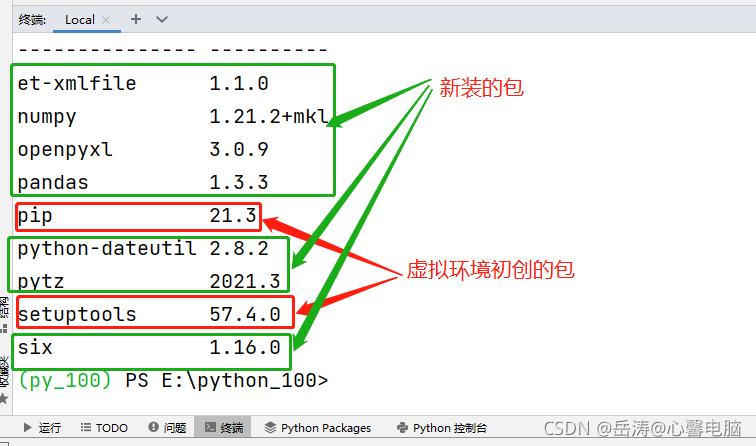
2.3 利用Pandas库输出到Excel,代码实现
# 九九乘法表
import pandas as pd
df = pd.DataFrame()
for i in range(1, 10):
for j in range(1, i+1):
if i*j < 10:
s_end = ' \t'
else:
s_end = '\t'
cell = f'{i}x{j} = {i*j}'
print(cell, end=s_end)
df.loc[i,j] = cell
print()
df = df.fillna('')
print(df)
df.to_excel('九九乘法表.xlsx')
输出结果:
1x1 = 1
2x1 = 2 2x2 = 4
3x1 = 3 3x2 = 6 3x3 = 9
4x1 = 4 4x2 = 8 4x3 = 12 4x4 = 16
5x1 = 5 5x2 = 10 5x3 = 15 5x4 = 20 5x5 = 25
6x1 = 6 6x2 = 12 6x3 = 18 6x4 = 24 6x5 = 30 6x6 = 36
7x1 = 7 7x2 = 14 7x3 = 21 7x4 = 28 7x5 = 35 7x6 = 42 7x7 = 49
8x1 = 8 8x2 = 16 8x3 = 24 8x4 = 32 8x5 = 40 8x6 = 48 8x7 = 56 8x8 = 64
9x1 = 9 9x2 = 18 9x3 = 27 9x4 = 36 9x5 = 45 9x6 = 54 9x7 = 63 9x8 = 72 9x9 = 81
1 2 3 ... 7 8 9
1 1x1 = 1 ...
2 2x1 = 2 2x2 = 4 ...
3 3x1 = 3 3x2 = 6 3x3 = 9 ...
4 4x1 = 4 4x2 = 8 4x3 = 12 ...
5 5x1 = 5 5x2 = 10 5x3 = 15 ...
6 6x1 = 6 6x2 = 12 6x3 = 18 ...
7 7x1 = 7 7x2 = 14 7x3 = 21 ... 7x7 = 49
8 8x1 = 8 8x2 = 16 8x3 = 24 ... 8x7 = 56 8x8 = 64
9 9x1 = 9 9x2 = 18 9x3 = 27 ... 9x7 = 63 9x8 = 72 9x9 = 81
[9 rows x 9 columns]
2.4 查看结果
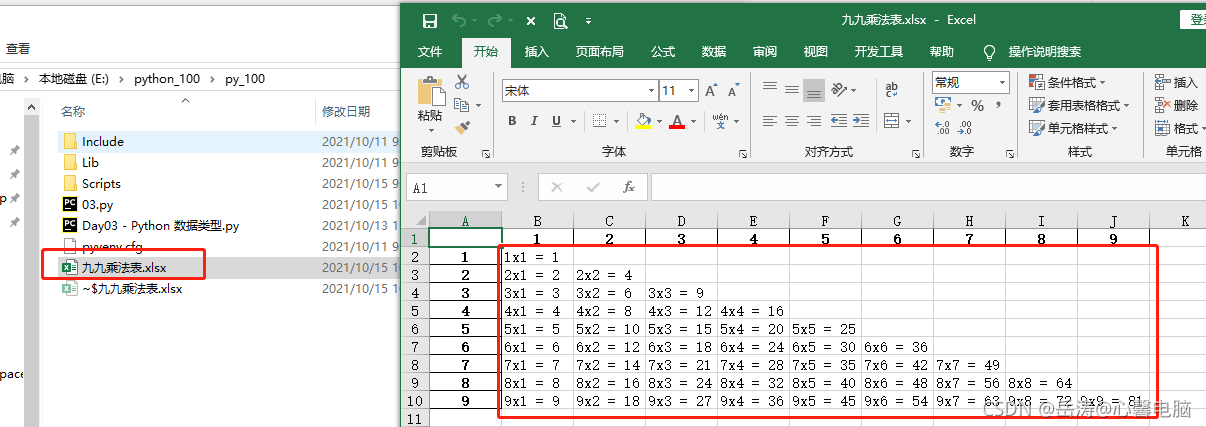
三、计算100以内的质数(素数)
3.1 需求分析
质数又称素数,是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。和质数相对的是合数,同时规定:1既不是质数又不是合数。
3.2 代码实现
3.2.1 原生算法
# 计算100以内的素数
import time
t1 = time.time()
lst_com = []
for i in range(2, 10001):
is_com = 0
for j in range(2, i):
if i % j == 0:
is_com = 1
if is_com == 1:
continue
# print(i)
lst_com.append(i)
print(lst_com)
t2 = time.time()
print(f'取出素数{len(lst_com)}个,耗时{t2-t1}秒。')
输出结果:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,..., 9931, 9941, 9949, 9967, 9973]
取出素数1229个,耗时7.759534120559692秒。
3.2.2 6K算法
任意一个合数都可分解为素数因子的乘积,观察素数的分布可以发现:除 2,3 以外的素数必定分布在 6k (k为大于1的整数) 的两侧。所以2,3外的素数形式只能写成 6k+1 或 6k-1的形式。据此,我们可以缩小因子范围。
# 计算100以内的素数
import math
import time
t1 = time.time()
lst_com = []
for i in range(2, 10001):
is_com = 0
if i ==2 or i == 3:
lst_com.append(i)
if i % 2 ==0 or i % 3 == 0:
continue
for j in range(6, int(math.sqrt(i))+2, 6):
if i % (j-1) == 0 or i % (j+1) == 0:
is_com = 1
if is_com == 1:
continue
# print(i)
lst_com.append(i)
print(lst_com)
t2 = time.time()
print(f'取出素数{len(lst_com)}个,耗时{t2-t1}秒。')
输出结果:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,..., 9931, 9941, 9949, 9967, 9973]
取出素数1229个,耗时0.04497265815734863秒。
3.3 算法的威力:方法比努力更重要
- 1万以内的素数,原生算法** 7.76 秒,6K算法 0.04 **秒,快了近200倍。
- 10万以内的素数,原生算法** 810.27 秒,6K算法 0.35 **秒,快了2300多倍。
- 素数算法除了6K算法,还有费马小定理算法、埃拉托斯特尼算法等。
原生算法输出结果:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,..., 99929, 99961, 99971, 99989, 99991]
取出素数9592个,耗时810.2736053466797秒。
6K算法输出结果:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,..., 99929, 99961, 99971, 99989, 99991]
取出素数9592个,耗时0.34779858589172363秒。