位置式PID与增量式PID的python实现
本文只展示部分代码,完整代码请访问我的github
一、PID控制器简介
PID(P比例,I积分,D微分)是一种model free的控制器,使用该控制器,无需对控制系统进行建立模型,只需对P、I 、D这三个参数进行调整即可,使用起来十分方便,因此在控制系统中被广泛使用。
u
(
t
)
=
K
p
e
(
t
)
+
K
i
∫
0
t
e
(
t
)
d
t
+
K
d
d
e
(
t
)
d
t
(1)
u(t) = K_pe(t) + K_i\int_{0}^{t} e(t)dt +K_d\frac{de(t)}{dt} \tag{1}
u(t)=Kp?e(t)+Ki?∫0t?e(t)dt+Kd?dtde(t)?(1)
- 积分项有助于消除稳态误差
- 微分项有助于加快系统相应
- PD控制:提高稳定性,改善瞬态响应
- PI控制:改善稳态误差
二、一阶惯性环节
以下的代码中将用一阶惯性环节作为被控对象来进行展开。此处简单介绍一下一阶惯性系统。
一阶惯性环节(系统)比较常见,如单容水箱、电容等含有储存元件或容量的元件系统,该系统输出一开始并不与输入同步按比例变化,直到过渡过程结束输出
y
(
t
)
y(t)
y(t)才与输入
x
(
t
)
x(t)
x(t)保持比例关系。
- 运动方程:
T d y ( t ) d t + y ( t ) = K x ( t ) T\frac{dy(t)}{dt} + y(t) = Kx(t) Tdtdy(t)?+y(t)=Kx(t) - 传递函数
G ( s ) = Y ( s ) X ( s ) = K T s + 1 G(s)= \frac{Y(s)}{X(s)} =\frac{K}{Ts +1} G(s)=X(s)Y(s)?=Ts+1K?
其中T是时间常数,K是比例常数 - 在数字控制系统中通常写为:
T [ y ( k ) ? y ( k ? 1 ) ] + y ( k ) = K x ( k ) T\left[y(k)-y(k-1) \right]+ y(k) = Kx(k) T[y(k)?y(k?1)]+y(k)=Kx(k) ? \Rightarrow ? y ( k ) = K x ( k ) + T y ( k ? 1 ) 1 + T y(k)= \frac{Kx(k)+Ty(k-1)}{1+T} y(k)=1+TKx(k)+Ty(k?1)?
三、位置式PID
3.1 简介
在计算机控制系统中往往使用位置式PID算法与增量式PID算法。下面给出位置式PID的公式。
u
(
k
)
=
K
p
e
(
k
)
+
K
i
∑
i
=
0
e
(
i
)
+
K
d
[
e
(
k
)
?
e
(
k
?
1
)
]
(2)
u(k) = K_pe(k) + K_i\sum_{i=0} e(i) +K_d\left[e(k)-e(k-1) \right] \tag{2}
u(k)=Kp?e(k)+Ki?i=0∑?e(i)+Kd?[e(k)?e(k?1)](2)
从公式可以看出,这就是对式(1)的直接数字化,容易理解,输出u(k)便是PID控制器的输出位置。
该控制器存在的缺点:
由于积分饱和带来的影响,控制器需要相当一段长的时间退出饱和区,由此引起系统产生大幅度超调。这里如果想继续了解积分饱和,请点击链接查看matlab官方的讲解。
3.2 python程序
#位置式PID系统
class PositionalPID:
def __init__(self, P: float, I: float, D: float):
self.Kp = P
self.Ki = I
self.Kd = D
self.PIDOutput = 0.0 # PID控制器输出
self.SystemOutput = 0.0 # 系统输出值
self.LastSystemOutput = 0.0 # 系统的上一次输出
self.PIDErrAdd = 0.0
self.ResultValueBack = 0.0
self.Error = 0.0
self.LastError = 0.0
def SetStepSignal(self, StepSignal):
self.Error = StepSignal - self.SystemOutput
KpWork = self.Kp *self.Error
KiWork = self.Ki* self.PIDErrAdd
KdWork = self.Kd * (self.Error- self.LastError)
self.PIDOutput = KpWork + KiWork + KdWork
self.PIDErrAdd += self.Error
self.LastError = self.Error
# 以一阶惯性环节为例子演示控制效果
def SetInertiaTime(self, IntertiaTime, SampleTime):
self.SystemOutput = (IntertiaTime * self.LastSystemOutput + SampleTime * self.PIDOutput) / (
SampleTime + IntertiaTime)
self.LastSystemOutput = self.SystemOutput
四、增量式PID
4.1简介
Δ
u
(
k
)
=
u
(
k
)
?
u
(
k
?
1
)
=
\Delta u(k) = u(k)-u(k-1)=
Δu(k)=u(k)?u(k?1)=
K
p
[
e
(
k
)
?
e
(
k
?
1
)
]
+
K
i
e
(
k
)
+
K
d
[
e
(
k
)
?
2
e
(
k
?
1
)
+
e
(
k
?
2
)
]
(3)
K_p\left[e(k)-e(k-1) \right] + K_i e(k) +K_d\left[e(k)-2e(k-1)+e(k-2) \right] \tag{3}
Kp?[e(k)?e(k?1)]+Ki?e(k)+Kd?[e(k)?2e(k?1)+e(k?2)](3)
增量式PID只求取控制量的变化量,一旦确定了 KP、TI 、TD,只要使用前后三次测量值的偏差, 即可由公式求出控制增量,而得出的控制量▲u(k)对应的是近几次位置误差的增量,而不是对应与实际位置的偏差,因此没有误差累加,容易通过加权处理获得比较好的控制效果,并且在系统发生问题时,增量式不会严重影响系统的工作。
最后的输出要加上上一时刻的输出u(k-1),即:
u
(
k
)
=
Δ
u
(
k
)
+
u
(
k
?
1
)
(4)
u(k)= \Delta u(k)+u(k-1)\tag{4}
u(k)=Δu(k)+u(k?1)(4)
4.2 python程序
#增量式PID系统
class IncrementalPID:
def __init__(self, P:float ,I:float ,D:float ):
self.Kp = P
self.Ki = I
self.Kd = D
self.PIDOutput =0.0 #PID控制器输出
self.SystemOutput = 0.0 #系统输出值
self.LastSystemOutput = 0.0 #系统的上一次输出
self.Error = 0.0
self.LastError = 0.0
self.LastLastError = 0.0
#设置PID控制器参数
def SetStepSignal(self,StepSignal):
self.Error = StepSignal - self.SystemOutput
#计算增量
IncrementalValue = self.Kp*(self.Error - self.LastError)\
+ self.Ki * self.Error +self.Kd *(self.Error -2*self.LastError +self.LastLastError)
#计算输出
self.PIDOutput += IncrementalValue
self.LastLastError = self.LastError
self.LastError = self.Error
#以一阶惯性环节为例子演示控制效果
def SetInertiaTime(self,IntertiaTime,SampleTime):
self.SystemOutput = (IntertiaTime*self.LastSystemOutput + SampleTime *self.PIDOutput)/(SampleTime + IntertiaTime)
self.LastSystemOutput = self.SystemOutput
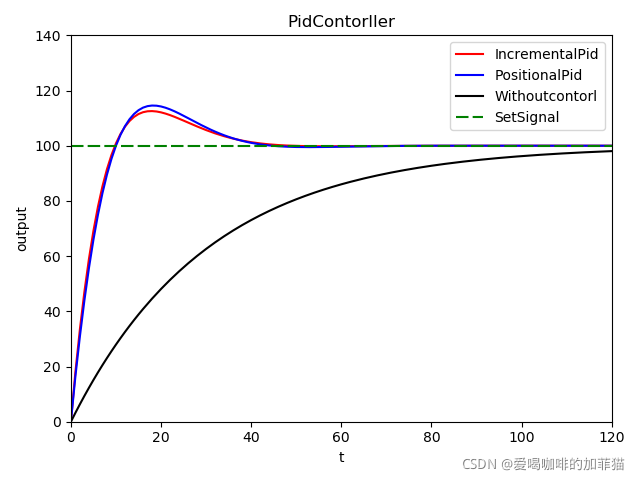
五、几种控制效果对比
上图!图中红色为增量式PID,蓝色为位置式PID,黑色是不加控制器的效果。