[Python知识库]【python】手写光线追踪教程

本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0

path tracer based on 《PBRT》

一.introduction to sampling theory

1. what is sampling?

impulse train：

sampling process corresponds to multiplying the function by a “impulse train” function, an infinite sum of equally spaced delta functions.

《PBRT》A digital image is represented as a set of pixel values, typically aligned on a rectangular grid. When a digital image is displayed on a physical device, these values are used to determine the spectral power emitted by pixels on the display.

《PBRT》the pixels that constitute an image are point samples of the image function at discrete points on the image plane.

there is no “area” associated with a pixel.

when sampling the film signal

pos = camera_pos
ray_dir = ti.Vector([
            (2 * fov * (u) / resolution[1] - fov * resolution[0] / resolution[1] - 1e-5),
            2 * fov * (v) / resolution[1] - fov - 1e-5, -1.0
        ]).normalized()

then we need anti-aliazing

pos = camera_pos
ray_dir = ti.Vector([
            (2 * fov * (u + ti.random()) / resolution[1] - fov * resolution[0] / resolution[1] - 1e-5),
            2 * fov * (v + ti.random()) / resolution[1] - fov - 1e-5, -1.0
        ]).normalized()

二.sampling

Preview (CDF sampling technique)

There are many techniques for generating random variates from a specified probability distribution such as the normal, exponential, or gamma distribution. However, one technique stands out because of its generality and simplicity: the inverse CDF sampling technique.

1. Uniformly Sampling a Hemisphere (multidimensional sampling technique)

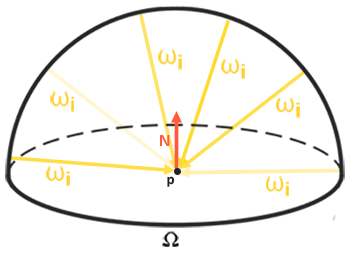
a uniform distribution means that the density function is a constant, so we know that p(x) = c

so p(ω) = 1/2*pi

then p(θ, φ) = sinθ/2*pi

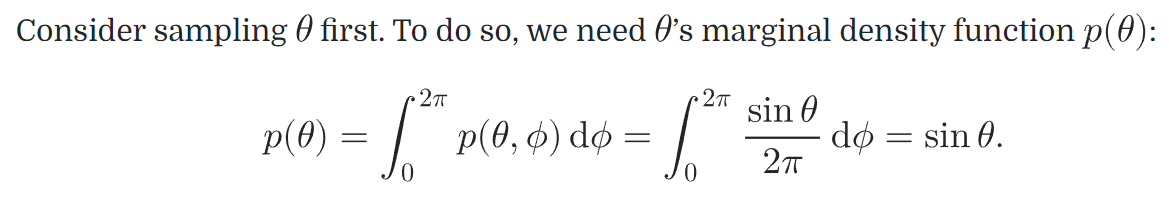
Notice that the density function for φ itself is uniform

then use the 1D inversion technique to sample each of these PDFs in turn

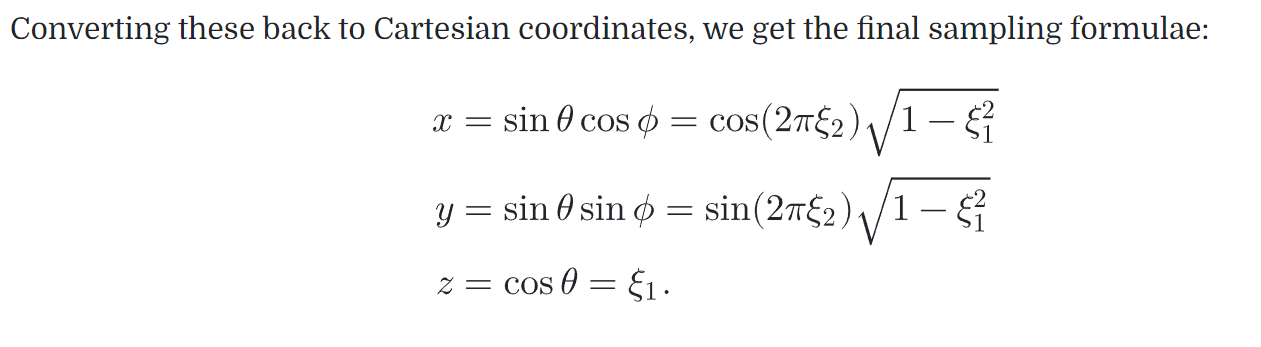
2. sample area light

def sample_area_light(hit_pos, pos_normal):
    # sampling inside the light area
    x = ti.random() * light_x_range + light_x_min_pos
    z = ti.random() * light_z_range + light_z_min_pos
    on_light_pos = ti.Vector([x, light_y_pos, z])
    return (on_light_pos - hit_pos).normalized()

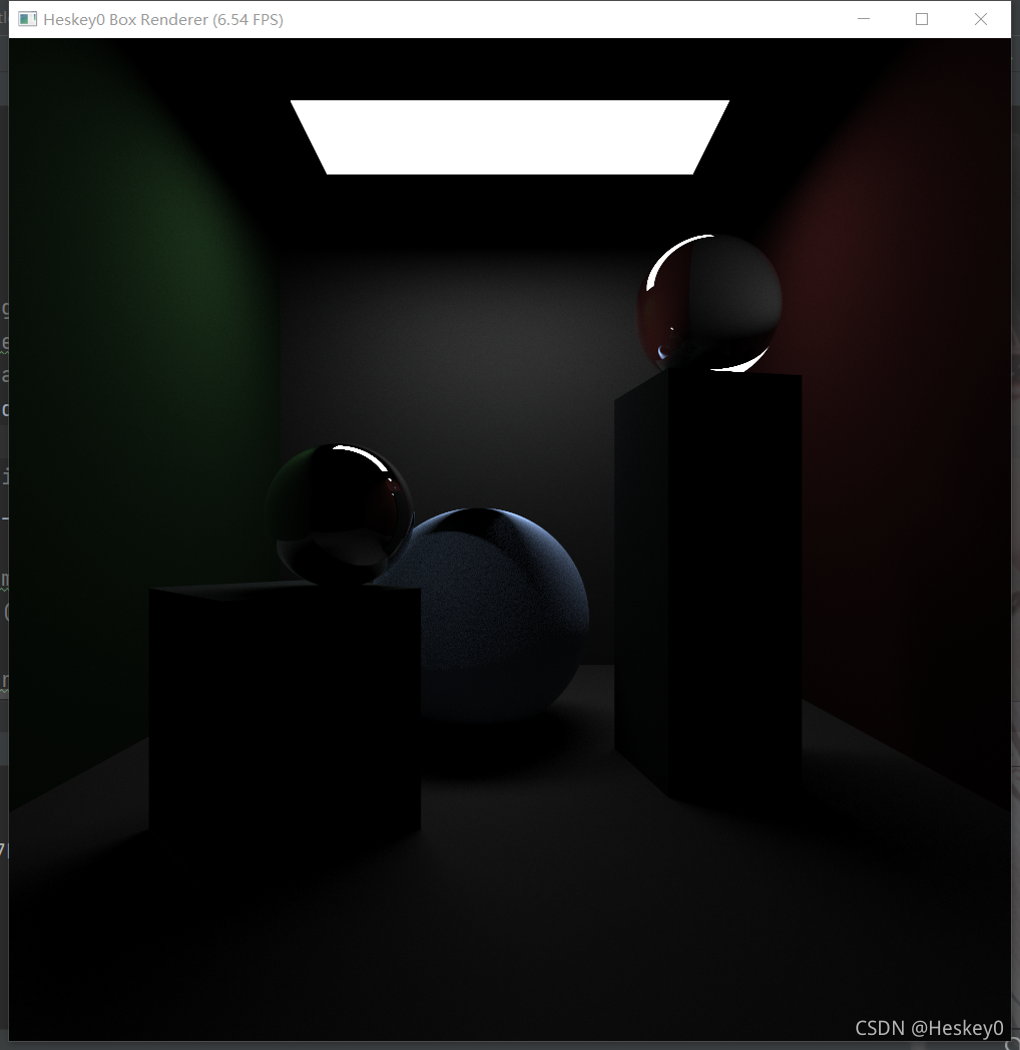
3. introduction to importance sampling

why we need importance sampling?

the Monte Carlo estimator converges more quickly if the samples are taken from a distribution p(x) that is similar to the function f(x) in the integrand.

《PBRT》：We will not provide a rigorous proof of this fact but will instead present an informal and intuitive argument.

then we try to analyze the importance sampling method

we have three terms

• BRDF
• incident radiance ( infeasible )
• cosine term

4. cosine-weighted sampling

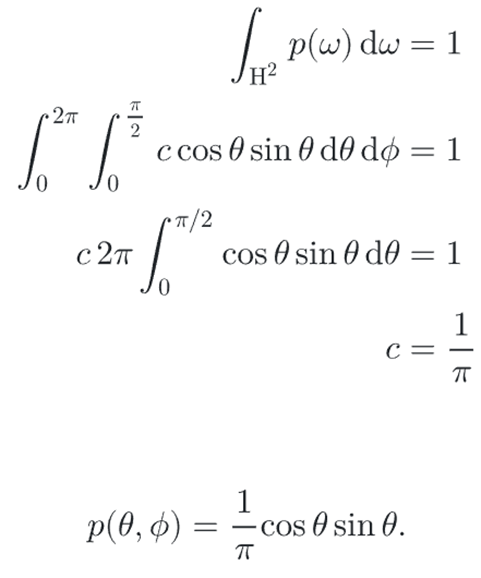
Malley’s method

So, We could compute the marginal and conditional densities as before, but instead we can use a technique known as Malley’s method to generate these cosine-weighted points.

1. cosine term

2. 2D Sampling with Multidimensional Transformations

   • (1) sampling a unit disk (Concentric Mapping)

   • (2) project up to the unit hemisphere (cosine-weighted hemisphere sampling)

(1) sampling a unit disk

(2) projection

To complete the (r,φ)=(sinθ,φ)?(θ,φ) transformation, we need the determinant of the Jacobian

Why

5. multiple importance sampling

BDPT only：

BDPT + MIS：

Why we need MIS?

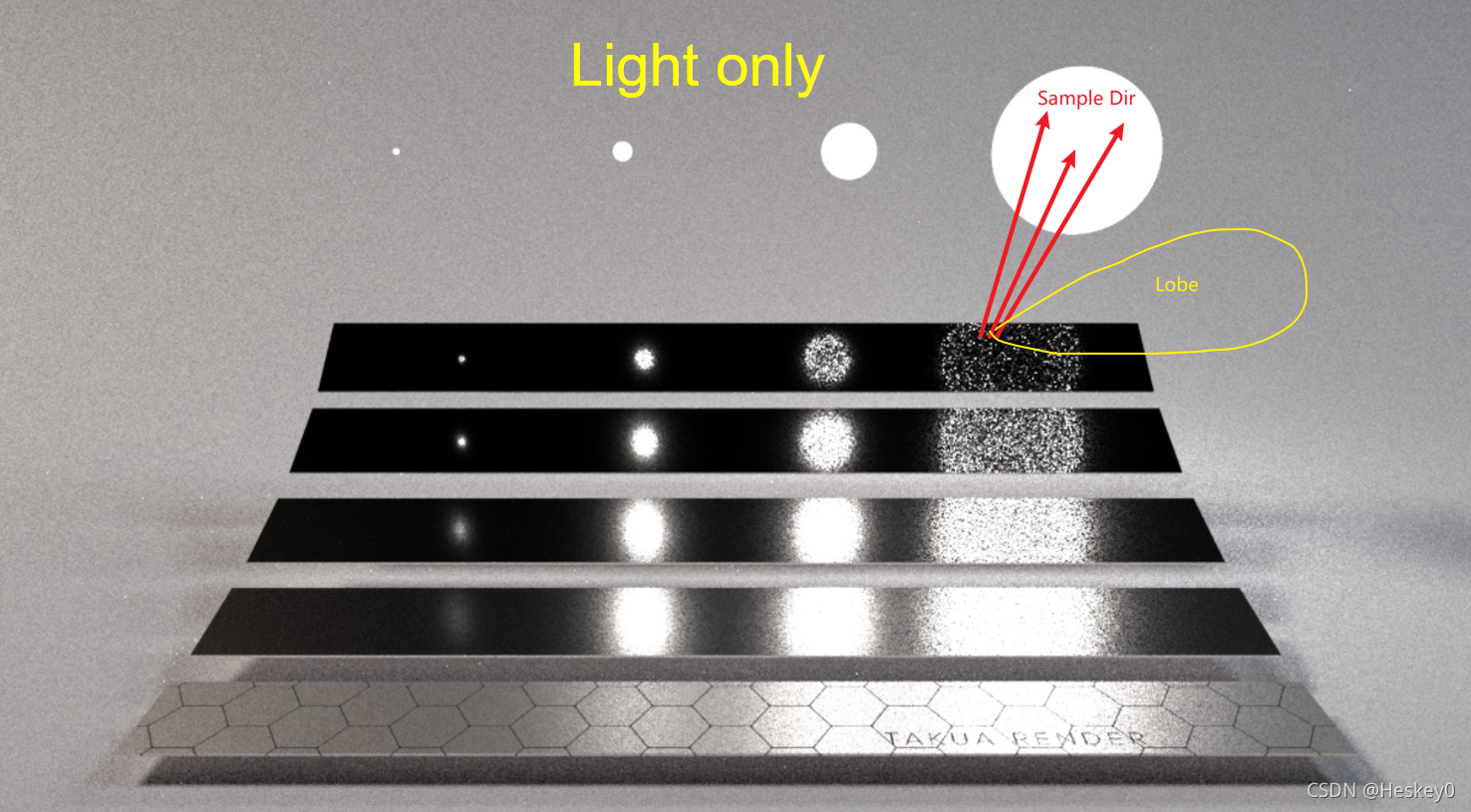
• balance heuristic

• power heuristic (Veach determined empirically that β=2 is a good value.)

//Compute heuristic
def mis_power_heuristic(pf, pg):
    # Assume 1 sample for each distribution
    f = pf ** 2
    g = pg ** 2
    return f / (f + g)
    # return 1

//combine
@ti.func
def sample_light_and_cosineWeighted(hit_pos, hit_normal):
    cosine_by_pdf = ti.Vector([0.0, 0.0, 0.0])

    light_pdf, cosineWeighted_pdf = 0.0, 0.0

    # sample area light => dir, light_pdf; then dir => lambertian_pdf; then mis
    light_dir = sample_area_light(hit_pos, hit_normal)
    if light_dir.dot(hit_normal) > 0:
        light_pdf = compute_area_light_pdf(hit_pos, light_dir)
        cosineWeighted_pdf = compute_cosineWeighted_pdf(hit_normal, light_dir)
        if light_pdf > 0 and cosineWeighted_pdf > 0:
            l_visible = visible_to_light(hit_pos, light_dir)
            if l_visible:
                heuristic = compute_heuristic(light_pdf, cosineWeighted_pdf)
                DoN = dot_or_zero(light_dir, hit_normal)
                cosine_by_pdf += heuristic * DoN / light_pdf

    # sample cosine weighted => dir, lambertian_pdf; then dir => light_pdf; then mis
    cosineWeighted_dir = cosine_weighted_sampling(hit_normal)
    cosineWeighted_pdf = compute_cosineWeighted_pdf(hit_normal, cosineWeighted_dir)
    light_pdf = compute_area_light_pdf(hit_pos, cosineWeighted_dir)
    if visible_to_light(hit_pos, cosineWeighted_dir):
        heuristic = compute_heuristic(cosineWeighted_pdf, light_pdf)
        DoN = dot_or_zero(cosineWeighted_dir, hit_normal)
        cosine_by_pdf += heuristic * DoN / cosineWeighted_pdf

    # direct_li = mis_weight * cosine / pdf
    return cosine_by_pdf

import taichi as ti
import numpy as np

ti.init(arch=ti.cuda)
resolution = (940, 940)

eps = 0.0001  # 浮点数精度
inf = 1e10

mat_none = 0
mat_lambertian = 1
mat_specular = 2    # 镜面
mat_glass = 3       # 玻璃
mat_light = 4
mat_microfacet = 5
mat_glossy = 6

# 光区域为一块板
light_y_pos = 2.0 - eps
light_x_min_pos = -0.7
light_x_range = 1.4
light_z_min_pos = 0.6
light_z_range = 0.4
light_area = light_x_range * light_z_range
light_min_pos = ti.Vector([
    light_x_min_pos,
    light_y_pos,
    light_z_min_pos])
light_max_pos = ti.Vector([
    light_x_min_pos + light_x_range,
    light_y_pos,
    light_z_min_pos + light_z_range
])
light_color = ti.Vector([1, 1, 1])
light_normal = ti.Vector([0.0, -1.0, 0.0])  # 光源方向向下


# 1.7700 : 红宝石的折射率
refract_index = 1.7700

# right sphere
sp1_center = ti.Vector([0.5, 1.18, 1.40])
sp1_radius = 0.18
# left sphere
sp2_center = ti.Vector([-0.35, 0.65, 1.70])
sp2_radius = 0.15
# middle sphere(microfacet)
sp3_center = ti.Vector([-0.10, 0.35, 1])
sp3_radius = 0.35
sp3_microfacet_roughness = 0.5
# sp3_idx = 1.55  # 石英晶体折射率
sp3_idx = 2.4  # 钻石折射率
# right front sphere(microfacet)
sp4_center = ti.Vector([-0.05, 1, 1])
sp4_radius = 0.3
sp4_microfacet_roughness = 1


# 构造变换矩阵，用于box
def make_box_transform_matrices(rotate_rad, translation):
    c, s = np.cos(rotate_rad), np.sin(rotate_rad)
    rot = np.array([[c, 0, s, 0],
                    [0, 1, 0, 0],
                    [-s, 0, c, 0],
                    [0, 0, 0, 1]])  # 绕y轴旋转67.5°
    # rot = np.array([[1, 0, 0, 0],
    #                 [0, c, s, 0],
    #                 [0,-s, c, 0],
    #                 [0, 0, 0, 1]])  # 绕y轴旋转67.5°
    translate = np.array([  # 平移 (0.5, 0, 1.4)
        [1, 0, 0, translation.x],
        [0, 1, 0, translation.y],
        [0, 0, 1, translation.z],
        [0, 0, 0, 1],
    ])
    m = translate @ rot  # 平移 + 旋转
    m_inv = np.linalg.inv(m)  # 逆矩阵
    m_inv_t = np.transpose(m_inv)  # 转置矩阵
    return ti.Matrix(m_inv), ti.Matrix(m_inv_t)  # 旋转-22.5° + 平移 (0.5, 0, 1)


# right box
box1_min = ti.Vector([0.0, 0.0, 0.0])
box1_max = ti.Vector([0.35, 1.0, 0.35])
box1_rotate_rad = np.pi / 16
box1_m_inv, box1_m_inv_t = make_box_transform_matrices(box1_rotate_rad, ti.Vector([0.30, 0, 1.20]))  # box的transform的 逆矩阵, 逆转置矩阵
# left box
box2_min = ti.Vector([0.0, 0.0, 0.0])
box2_max = ti.Vector([0.4, 0.5, 0.4])
box2_rotate_rad = np.pi / 4
box2_m_inv, box2_m_inv_t = make_box_transform_matrices(box2_rotate_rad, ti.Vector([-0.75, 0, 1.70]))  # box的transform的 逆矩阵, 逆转置矩阵


'''
lambertian brdf
'''
# No absorbtion     没有吸收光谱，Albedo为1，对单位半球积分
lambertian_brdf = 1.0 / np.pi  # f(lambert) = k*c / π       # k = 1,  c = hit_color*light_color


'''
microfacet brdf
'''
# compute reflectance
# 计算反射比
@ti.func
def schlick(cos, eta):  # 入射角cosine, 折射率refractive index
    r0 = (1.0 - eta) / (1.0 + eta)
    r0 = r0 * r0  # 反射比 reflectance
    return r0 + (1 - r0) * ((1.0 - cos) ** 5)


# normal distribution function
@ti.func
def ggx(alpha, i_dir, o_dir, n_dir):  # roughness, incident, exit, normal
    m_dir = (i_dir + o_dir).normalized()
    cos_theta_square = m_dir.dot(n_dir)
    tan_theta_square = (1-cos_theta_square) / cos_theta_square
    root = alpha / cos_theta_square * (alpha*alpha + tan_theta_square)
    return root*root / np.pi


@ti.func
def ggx2(alpha, i_dir, o_dir, n_dir):
    m_dir = (i_dir + o_dir).normalized()
    NoM = n_dir.dot(m_dir)
    d = NoM*NoM * (alpha*alpha-1) + 1
    return alpha*alpha / np.pi*d*d


@ti.func
def smithG1(alpha, v_dir, n_dir):
    out = 0.0
    # compute tan_theta(v / n)
    cos_theta_square = v_dir.dot(n_dir) ** 2
    tan_theta_square = (1-cos_theta_square) / cos_theta_square
    tan_theta = ti.sqrt(tan_theta_square)
    if tan_theta == 0:
        out = 1
    else:
        root = alpha * tan_theta
        out = 2 / (1 + ti.sqrt(1.0 + root * root))

    return out


@ti.func
# shadowing-masking
def smith(alpha, i_dir, o_dir, n_dir):  # roughness, incident, exit, normal
    # m_dir = (i_dir + o_dir).normalized()
    # shadowing * masking
    return smithG1(alpha, i_dir, n_dir) * smithG1(alpha, o_dir, n_dir)


@ti.func
def compute_microfacet_brdf(alpha, idx, i_dir, o_dir, n_dir):
    micro_cos = o_dir.dot((i_dir + o_dir).normalized())
    # numerator and denominator
    D = ggx2(alpha, i_dir, o_dir, n_dir)
    G = smith(alpha, i_dir, o_dir, n_dir)
    F = schlick(micro_cos, idx)
    # print(D, G, F)

    numerator = D * G * F
    denominator = 4 * o_dir.dot(n_dir) * i_dir.dot(n_dir)
    cook_torrance = numerator / ti.abs(denominator)
    return cook_torrance


'''
basic functions
'''
# 反射
@ti.func
def reflect(d, n):
    # d and n are both normalized
    ret = d - 2.0 * d.dot(n) * n  # d - 2*|d|*|n|*n*cos<d,n>(theta) = d - 2 |d|*cos(theta) * (n/|n|)
    return ret  # reflect vector


# 折射
@ti.func
def refract(d, n, ni_over_nt):
    dt = d.dot(n)  # cos    # sin**2 = 1 - cos**2
    discr = 1.0 - ni_over_nt * ni_over_nt * (1.0 - dt * dt)  # discr:折射角的cos
    rd = (ni_over_nt * (d - n * dt) - n * ti.sqrt(discr)).normalized()
    return rd  # 是否有反射光, 反射光方向


# 点由矩阵变换
@ti.func
def mat_mul_point(m, p):
    hp = ti.Vector([p[0], p[1], p[2], 1.0])
    hp = m @ hp
    hp /= hp[3]
    return ti.Vector([hp[0], hp[1], hp[2]])


# [3] => ti.Vector(4);   m@v  # [4, 4]@[4]
# 忽略矩阵的第4行第4列, 忽略矩阵的平移
@ti.func
def mat_mul_vec(m, v):
    hv = ti.Vector([v[0], v[1], v[2], 0.0])
    hv = m @ hv
    return ti.Vector([hv[0], hv[1], hv[2]])


# 判断射线与球是否相交
@ti.func
def intersect_sphere(pos, d, center, radius):  # pos:light_position, d:ray_dir
    # 构建余弦定理三角形:判断光与球是否相交
    T = pos - center
    A = 1.0
    B = 2.0 * T.dot(d)
    C = T.dot(T) - radius * radius
    delta = B * B - 4.0 * A * C
    dist = inf
    hit_pos = ti.Vector([0.0, 0.0, 0.0])

    if delta > 0:  # 有解
        delta = ti.max(delta, 0)
        sdelta = ti.sqrt(delta)
        ratio = 0.5 / A
        ret1 = ratio * (-B - sdelta)  # 方程的解, 即三角形的边长(离入射光近的点)
        dist = ret1
        hit_pos = pos + d * dist

    return dist, hit_pos  # 光源到命中点的距离, 命中点坐标


# plane
@ti.func
def intersect_plane(pos, d, pt_on_plane, norm):  # position, ray_dir, offset, normal
    dist = inf
    hit_pos = ti.Vector([0.0, 0.0, 0.0])
    denom = d.dot(norm)
    if abs(denom) > eps:  # 光与平面不平行
        dist = norm.dot(pt_on_plane - pos) / denom
        hit_pos = pos + d * dist
    return dist, hit_pos  # 光源到命中点的距离, 命中点坐标


# 参考清华大学图形学课程中的基于slab的求交算法：Liang_Barsky算法
# aabb包围体 call by intersect_box and intersect_light
@ti.func
def intersect_aabb(box_min, box_max, o, d):  # box_min, box_max, pos(box空间), ray_dir(box空间)
    intersect = 1  # 光与box是否相交

    near_t = -inf
    far_t = inf
    near_face = 0
    near_is_max = 0

    for i in ti.static(range(3)):  # ti.static(range()) can iterate matrix elements
        if d[i] == 0:  # 光平行于包围体的一个面
            if o[i] < box_min[i] or o[i] > box_max[i]:
                intersect = 0
        else:
            i1 = (box_min[i] - o[i]) / d[i]  # 除以d[i] : 判断光是否正对box
            i2 = (box_max[i] - o[i]) / d[i]

            new_far_t = max(i1, i2)     # 光朝着正半轴时，为i2
            new_near_t = min(i1, i2)    # 光朝着正半轴时，为i1
            new_near_is_max = i2 < i1   # 光朝着负半轴时(near_t取i2)，为true

            far_t = min(new_far_t, far_t)  # far_t 取最小
            if new_near_t > near_t:  # near_t 取最大
                near_t = new_near_t
                near_face = int(i)  # 记录最小的i所在的维
                near_is_max = new_near_is_max  # 在当前维中near_t, i2<i1 ?

    near_norm = ti.Vector([0.0, 0.0, 0.0])
    if near_t > far_t:
        intersect = 0
    if intersect:
        for i in ti.static(range(2)):
            if near_face == i:
                near_norm[i] = -1 + near_is_max * 2     # near_is_max => return 1; else => return -1
    return intersect, near_t, far_t, near_norm  # 是否相交, 首先相交的平面的距离, 远平面, 近平面法线


# params: min, max, position, ray_dir
# box
@ti.func
def intersect_aabb_transformed(box_m_inv, box_m_inv_t, box_min, box_max, o, d):
    # 射线转换到包围体的local position
    obj_o = mat_mul_point(box_m_inv, o)
    obj_d = mat_mul_vec(box_m_inv, d)

    intersect, near_t, _, near_norm = intersect_aabb(box_min, box_max, obj_o, obj_d)
    # print(near_norm)
    if intersect and 0 < near_t:
        near_norm = mat_mul_vec(box_m_inv_t, near_norm)
    else:
        intersect = 0
    # out params: hit?, cur_dist, pnorm
    return intersect, near_t, near_norm


# light
@ti.func
def intersect_light(pos, ray_dir, tmax):
    # t:near intersect distance
    hit, t, far_t, near_norm = intersect_aabb(light_min_pos, light_max_pos, pos, ray_dir)
    if hit and 0 < t < tmax:
        hit = 1
    else:
        hit = 0
        t = inf
    return hit, t


# 光线与场景相交
@ti.func
def intersect_scene(pos, ray_dir):
    # closest:深度缓冲区
    closest, normal = inf, ti.Vector.zero(ti.f32, 3)
    # color, material
    c, mat = ti.Vector.zero(ti.f32, 3), mat_none

    # right sphere
    cur_dist, hit_pos = intersect_sphere(pos, ray_dir, sp1_center, sp1_radius)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = (hit_pos - sp1_center).normalized()
        c, mat = ti.Vector([1.0, 1.0, 1.0]), mat_glass

    # middle Sphere
    cur_dist, hit_pos = intersect_sphere(pos, ray_dir, sp3_center, sp3_radius)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = (hit_pos - sp3_center).normalized()
        c, mat = ti.Vector([102.0/255.0, 153.0/255.0, 255.0/255.0]), mat_microfacet

    # left Sphere
    cur_dist, hit_pos = intersect_sphere(pos, ray_dir, sp2_center, sp2_radius)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = (hit_pos - sp2_center).normalized()
        c, mat = ti.Vector([1.0, 1.0, 1.0]), mat_specular

    # left box
    hit, cur_dist, pnorm = intersect_aabb_transformed(box2_m_inv, box2_m_inv_t, box2_min, box2_max, pos, ray_dir)
    if hit and 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = ti.Vector([0.8, 1, 1]), mat_lambertian

    # right box
    hit, cur_dist, pnorm = intersect_aabb_transformed(box1_m_inv, box1_m_inv_t, box1_min, box1_max, pos, ray_dir)
    if hit and 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = ti.Vector([0.8, 1, 1]), mat_lambertian

    # left plane
    pnorm = ti.Vector([1.0, 0.0, 0.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([-1.1, 0.0, 0.0]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = ti.Vector([60.0 / 255.0, 200.0 / 255.0, 60 / 255.0]), mat_lambertian
    # right plane
    pnorm = ti.Vector([-1.0, 0.0, 0.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([1.1, 0.0, 0.0]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = ti.Vector([200.0 / 255.0, 30.0 / 255.0, 30 / 255.0]), mat_lambertian
    # bottom plane
    gray = ti.Vector([0.93, 0.93, 0.93])
    pnorm = ti.Vector([0.0, 1.0, 0.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([0.0, 0.0, 0.0]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = gray, mat_lambertian
    # top
    pnorm = ti.Vector([0.0, -1.0, 0.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([0.0, 2.0, 0.0]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = gray, mat_lambertian
    # far
    pnorm = ti.Vector([0.0, 0.0, 1.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([0.0, 0.0, 0.0]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = gray, mat_lambertian
    # close
    pnorm = ti.Vector([0.0, 0.0, -1.0])
    cur_dist, _ = intersect_plane(pos, ray_dir, ti.Vector([0.0, 0.0, 3]), pnorm)
    if 0 < cur_dist < closest:  # 深度测试
        closest = cur_dist
        normal = pnorm
        c, mat = ti.Vector([0, 0, 0]), mat_lambertian

    # light
    hit_l, cur_dist = intersect_light(pos, ray_dir, closest)
    if hit_l and 0 < cur_dist < closest:  # 深度测试
        # no need to check the second term
        closest = cur_dist
        normal = light_normal
        c, mat = light_color, mat_light

    return closest, normal, c, mat


# 判断ray_dir是否与光源相交
@ti.func
def visible_to_light(pos, ray_dir):
    # eps*ray_dir to prevent rounding error
    a, b, c, mat = intersect_scene(pos + eps * ray_dir, ray_dir)
    return mat == mat_light


@ti.func
def dot_or_zero(n, l):
    return max(0.0, n.dot(l))











# TODO:begin
# '''
# sampling functions

# multiple importance sampling
@ti.func
def compute_heuristic(pf, pg):
    # Assume 1 sample for each distribution
    f = pf ** 2
    g = pg ** 2
    return f / (f + g)


# 已知sample dir
# area light pdf
@ti.func
def compute_area_light_pdf(pos, ray_dir):
    hit_l, t = intersect_light(pos, ray_dir, inf)
    pdf = 0.0
    if hit_l:  # ray_dir命中了灯光
        l_cos = light_normal.dot(-ray_dir)  # 光源的方向 与 ray_dir 的夹角cosine
        if l_cos > eps:  # 光源 与 ray_dir 同向
            tmp = ray_dir * t
            dist_sqr = tmp.dot(tmp)
            pdf = dist_sqr / (light_area * l_cos)
    return pdf


# 已知sample dir
# cosine weighted sampling
@ti.func
def compute_cosineWeighted_pdf(normal, sample_dir):
    return dot_or_zero(normal, sample_dir) / np.pi  # p(theta, phi) = cos(theta) * sin(theta) / pi


# 未知sample dir
# sample light
@ti.func
def sample_area_light(hit_pos, pos_normal):
    # sampling inside the light area
    x = ti.random() * light_x_range + light_x_min_pos
    z = ti.random() * light_z_range + light_z_min_pos
    on_light_pos = ti.Vector([x, light_y_pos, z])
    return (on_light_pos - hit_pos).normalized()


# 未知sample dir
# Cosine-Weighted Sampling
@ti.func
def cosine_weighted_sampling(normal):
    r, phi = 0.0, 0.0  # 圆上的 (r, theta) 在半球里实际上是 (sin(theta), phi) ，将其变换到 (theta, phi)
    sx = ti.random() * 2.0 - 1.0  # -1 ~ 1 random
    sy = ti.random() * 2.0 - 1.0  # -1 ~ 1 random
    # 1.concentric sample
    # sample on a unit disk
    if sx != 0 or sy != 0:
        if abs(sx) > abs(sy):
            r = sx
            phi = np.pi / 4 * (sy / sx)
        else:
            r = sy
            phi = np.pi / 4 * (2 - sx / sy)

    # 2.apply Malley's method
    # project disk to hemisphere

    # 由normal为中心轴,u和v为水平轴建立笛卡尔坐标系
    # 不需要关心normal和vector.up的关系，vector.up的引入是为了辅助建立起坐标系(u,v,normal)
    u = ti.Vector([1.0, 0.0, 0.0])
    if abs(normal[1]) < 1 - eps:
        u = normal.cross(ti.Vector([0.0, 1.0, 0.0]))  # normal x vector.up = sin(eta)
    v = normal.cross(u)  # normal x u = |u| = sin(eta)

    # theta : vector.up 与 normal 的夹角
    # u,v垂直, 长度均为sin(phi), 均在微平面上

    xy = r * ti.cos(phi) * u + r * ti.sin(phi) * v  # 采样时的x,y,normal坐标系转换到u,v,normal坐标系(采样点随之旋转并变为sin(eta)倍)
    zlen = ti.sqrt(max(0.0, 1.0 - xy.dot(xy)))  # zlen:采样线沿normal的长度

    return xy + zlen * normal  # sample dir


# 两种pdf相乘, 结果为对光采样
# sample direct light
@ti.func
def sample_light_and_cosineWeighted(hit_pos, hit_normal):
    cosine_by_pdf = ti.Vector([0.0, 0.0, 0.0])

    light_pdf, cosineWeighted_pdf = 0.0, 0.0

    # sample area light => dir, light_pdf; then dir => lambertian_pdf; then mis
    light_dir = sample_area_light(hit_pos, hit_normal)
    if light_dir.dot(hit_normal) > 0:
        light_pdf = compute_area_light_pdf(hit_pos, light_dir)
        cosineWeighted_pdf = compute_cosineWeighted_pdf(hit_normal, light_dir)
        if light_pdf > 0 and cosineWeighted_pdf > 0:
            l_visible = visible_to_light(hit_pos, light_dir)
            if l_visible:
                heuristic = compute_heuristic(light_pdf, cosineWeighted_pdf)
                DoN = dot_or_zero(light_dir, hit_normal)
                cosine_by_pdf += heuristic * DoN / light_pdf

    # sample cosine weighted => dir, lambertian_pdf; then dir => light_pdf; then mis
    cosineWeighted_dir = cosine_weighted_sampling(hit_normal)
    cosineWeighted_pdf = compute_cosineWeighted_pdf(hit_normal, cosineWeighted_dir)
    light_pdf = compute_area_light_pdf(hit_pos, cosineWeighted_dir)
    if visible_to_light(hit_pos, cosineWeighted_dir):
        heuristic = compute_heuristic(cosineWeighted_pdf, light_pdf)
        DoN = dot_or_zero(cosineWeighted_dir, hit_normal)
        cosine_by_pdf += heuristic * DoN / cosineWeighted_pdf

    # direct_li = mis_weight * cosine / pdf
    return cosine_by_pdf



@ti.func
def sample_ray_dir(indir, normal, hit_pos, mat):
    u = ti.Vector([0.0, 0.0, 0.0])  # 用于下一次追踪的ray_dir
    pdf = 1.0
    if mat == mat_lambertian:
        u = cosine_weighted_sampling(normal)  # sample brdf : return ray_dir
        pdf = max(eps, compute_cosineWeighted_pdf(normal, u))  # 计算在该方向采样射线的pdf
    elif mat == mat_glossy:
        pass
    elif mat == mat_microfacet:
        # TODO:对cosine项采样
        u = cosine_weighted_sampling(normal)  # sample brdf : return ray_dir
        pdf = max(eps, compute_cosineWeighted_pdf(normal, u))  # 计算在该方向采样射线的pdf

    elif mat == mat_specular:  # 反射, pdf = 1
        u = reflect(indir, normal)
    elif mat == mat_glass:  # 折射, 反射, pdf = 1
        cos = indir.dot(normal)  # indir和normal的夹角 (indir和normal为单位向量)
        ni_over_nt = refract_index  # ni / nt = 折射率
        outn = normal
        if cos > 0.0:
            outn = -normal
            cos = refract_index * cos  # 出射角度
        else:
            ni_over_nt = 1.0 / refract_index
            cos = -cos  # indir转180°

        refl_prob = schlick(cos, refract_index)  # Fresnel reflectance
        if ti.random() < refl_prob:  # 反射的能量
            u = reflect(indir, normal)
        else:  # 折射的能量
            u = refract(indir, outn, ni_over_nt)
    return u.normalized(), pdf  # 用于下一次追踪的ray_dir, pdf


pixels = ti.Vector.field(3, dtype=ti.f32, shape=resolution)

camera_pos = ti.Vector([0.0, 0.6, 3.0])
fov = 0.8

max_bounce = 10


@ti.kernel
def render():
    for u, v in pixels:  # 遍历像素
        pos = camera_pos
        ray_dir = ti.Vector([
            (2 * fov * (u + ti.random()) / resolution[1] - fov * resolution[0] / resolution[1] - 1e-5),
            2 * fov * (v + ti.random()) / resolution[1] - fov - 1e-5, -1.0
        ]).normalized()

        final_throughput = ti.Vector([0.0, 0.0, 0.0])  # 累加到pixels
        throughput = ti.Vector([1.0, 1.0, 1.0])  # Lighting : (r, g, b)

        # 追踪开始
        bounce = 0
        while bounce < max_bounce:  # bounce的最大次数
            bounce += 1
            # closest:光源到物体的距离
            closest, hit_normal, hit_color, mat = intersect_scene(pos, ray_dir)  # 光发出后碰到场景

            # 0.命中灯光或无材质, 则中断追踪
            if mat == mat_none:
                final_throughput += throughput * 0
                break
            if mat == mat_light:
                final_throughput += throughput * light_color
                break

            hit_pos = pos + closest * ray_dir
            ray_dir_i = -ray_dir

            # 1.计算采样后的ray_dir, pdf

            # 2.lambertian : sample direct light [ mis(sample area light, sample brdf)=> Li ]
            if mat == mat_lambertian:  # lambertian模型
                final_throughput += light_color * throughput * lambertian_brdf * hit_color * sample_light_and_cosineWeighted(hit_pos, hit_normal)
                # Sample Direct Light Only
                # throughput *= sample_light_and_cosineWeighted(hit_pos, hit_normal, hit_color)

            # 2.lambertian : sample cosine-Weighted
            ray_dir, pdf = sample_ray_dir(ray_dir, hit_normal, hit_pos, mat)  # 由反射更新ray_dir
            pos = hit_pos + eps * ray_dir
            if mat == mat_lambertian:  # lambertian
                # f(lambert) * max(0.0, cos(n,l)) / pdf
                # throughput : Li or Lo
                throughput *= (lambertian_brdf * hit_color) * dot_or_zero(hit_normal, ray_dir) / pdf

            # 3.specular全反射
            if mat == mat_specular:
                throughput *= hit_color
            # 4.glass折射btdf
            if mat == mat_glass:
                throughput *= hit_color

            # 5.microfacet
            if mat == mat_microfacet:
                # compute_microfacet_brdf params:(alpha, idx, i_dir, o_dir, n_dir)
                cook_torrance_brdf = compute_microfacet_brdf(sp3_microfacet_roughness, sp3_idx, ray_dir_i, ray_dir, hit_normal)
                # print(lambertian_brdf, cook_torrance_brdf)

                microfacet_brdf = lambertian_brdf + cook_torrance_brdf  # TODO:BUG 黑屏

                throughput *= (microfacet_brdf * hit_color) * dot_or_zero(hit_normal, ray_dir) / pdf

            # 6.glossy
            if mat == mat_glossy:  #
                throughput *= (lambertian_brdf * hit_color) * dot_or_zero(hit_normal, ray_dir) / pdf




        pixels[u, v] += final_throughput


gui = ti.GUI('Path Tracing', resolution)
i = 0

while gui.running:
    # if gui.get_event(ti.GUI.PRESS):
    #     if gui.event.key == 'w':
    #         gui.clear()
    #         i = 0
    #         interval = 10
    #         # pixels = ti.Vector.field(3, dtype=ti.f32, shape=resolution)  # 屏幕像素缓冲 [800, 800] 元素为(r, g, b)
    #         count_var = ti.field(ti.i32, shape=(1,))
    #         box1_rotate_rad += np.pi/8

    if gui.get_event(ti.GUI.PRESS):
        if gui.event.key == 'w':
            img = pixels.to_numpy()
            img = np.sqrt(img / img.mean() * 0.24)
            fname = f'cornell_box.png'
            ti.imwrite(img, fname)
            print("图片已存储")

    render()
    interval = 10  # render()10次, 绘1次图
    if i % interval == 0 and i > 0:
        img = pixels.to_numpy()
        img = np.sqrt(img / img.mean() * 0.24)
        gui.set_image(img)

        gui.show()
    i += 1

本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0