????????采用某种函数逼近的缺点是事先经常不清楚何种函数对真实情况最符合。实际上，逼近平滑问题属于概率论的范畴，即如何从观测值寻求最可几值[1]。最合适的曲线应该是“绝对逼真”和“绝对平滑”之间某种折中的曲线[1-4]。
一、发展
????????1923年，Whittaker将光滑度与拟合度做了线性组合，发展为Whittaker修匀：
式中，F为拟合度（或逼真度），F越小越好，F越小说明拟合效果越好，即与原数据偏离越小；当F=0时，说明修匀值与原观测值完全重合，此时并没有得到起到修匀效果。S是光滑度（或粗糙度），S越小说明曲线越平滑；单独考虑S=0时，所有的平滑值位于一条直线上。h是正常数。n是数据量。pi为观测值的权。yi是为观测值。yi-是平滑值。z是差分的阶数。在满足上述准则下所获得的修匀值既满足位于一条光滑的曲线上，又与原观测序列具有一定的拟合度，即偏离较小。
????????1967年，捷克天文学家Vondrak将Whittaker修匀中原定义的平滑度为平滑值的Z阶差分的平方和 改进为 以平滑值的3阶差分的平方和 代替[2]，从而发展为Whittaker-Vondrak平滑法，简称Vondrak滤波。Vondrak平滑的基本准则是：
????????1976年，Vondrak对上述准则进行了改进和发展，即将上式中的拟合度和平滑度分别用他们的平均值来代替[3]：
式中，
是一个给定的无量纲的正数，定义为平滑因子，在观测数据的绝对拟合和绝对平滑之间起着平衡作用，ε越小，曲线的平滑程度越强，反之，平滑程度越弱。如果λ2=0，那么y=y’，即“绝对逼真”；如果λ2=∞，则有S=0，F=min，解是一条二次抛物线，即“绝对平滑”。因此，采用不同的λ值，得到的是这两种极端情况之间不同程度的折中曲线曲线[4]。
二、方法特性
????????Vondrak滤波方法的特点：在未知拟合函数的情况下，对观测资料进行合理的平滑[2]。
????????事实上，Vondrak滤波方法是一种联合分布，是由测量资料的正态分布和三阶差分的先验分布（即约束条件）所组成的联合分布。这种平滑分布的基本思想就是使这种联合分布达到极小值，从而来估计测量数据合理的平滑曲线。与其它平滑方法相比较，该方法的主要优点是：不需要确定拟合函数；不损失资料两端的平滑值；适用于等间距和不等间距的测量资料；还可作为分离测量资料中不同频率信号的数字滤波器[5，6]。
三、头疼的公式[7，8，9]
3.1 公式推导
? ? ? ? 公式太多，有时间再写。
3.2 最小二乘解
????????（1）最小二乘求解需满足：
?
式中，E是单位矩阵，
，
，
，
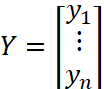????????（2）Q对y-求导得：
????????（3）化简得：
四、代码
分享给有需要的人，代码质量勿喷
import numpy as np
import matplotlib.pyplot as plt
def Vondrak(x, y, λ2):
n = len(x)
E = np.eye(n)
A = np.zeros((n-3, n))
valueA = np.array([-1, 3, -3, 1]).reshape((1, 4))
for r in range(n - 3):
A[r, [r, r + 1, r + 2, r + 3]] = valueA
AT = np.transpose(A) # AT = A.T
temp = E + ((n-3)/n) * λ2 * (AT.dot(A))
temp_inv = np.linalg.inv(temp)
y_Vondrak = temp_inv.dot(y)
return y_Vondrak
if __name__ == '__main__':
#region data
t = np.linspace(start = 0, stop = 100, num = 100)
y_sin = np.sin(0.1*t)
y_noise = np.sin(0.1*t) + np.random.randn(len(t)) * 0.3
# endregion
#region xj_Vondrak：λ2 越大越平滑
λ2 = 1 #越大越平滑
y_Vondrak_λ2_small = Vondrak(t, y_noise, λ2/10000)
y_Vondrak_λ2 = Vondrak(t, y_noise, λ2)
y_Vondrak_λ2_big = Vondrak(t, y_noise, λ2*1000000)
#endregion
#region plot
plt.plot(t, y_noise,"ko")
plt.plot(t, y_Vondrak_λ2_small, "r-")
plt.plot(t, y_Vondrak_λ2, "g-",linewidth=2)
plt.plot(t, y_Vondrak_λ2_big, "b--",linewidth=2)
# show
plt.title("Vondrak")
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend([
'points',
'Vondrak λ2 = 0.0001',
'Vondrak λ2 = 1',
'Vondrak λ2 = 1000000',
])
plt.grid(True)
plt.show()
#endregion五、试验结果
参考
[1] 董大南,郑大伟.Vondrak滤波器的端部效应[J].中国科学院上海天文台年刊,1985(00):13-25.
[2] Vondrak J. A contribution to the problem of smoothing observational data[J]. Bulletin of the Astronomical Institutes of Czechoslovakia, 1969, 20(06): 349-355.
[3] Vondrak J. Problem of smoothing observational data II[J]. Bulletin of the Astronomical Institutes of Czechoslovakia, 1977, 28(02): 84-89.
[4] 黄坤仪,周雄.Whittaker-Vondrak法滤波本质的探讨和数值滤波的方差与相关性估计[J].天文学报,1981(02):120-130.
[5] Zheng D. Discussion on selecting the smooth factor using cross-validation technique[J]. Annual of Shanghai Astronomical Observatory Chinese Academy of Sci-ences, 1988: 23-26.
[6] Zheng D, Luo S. Contribution of time series analysis to data processing of astronomical observations in China[J]. Statistica Sinica, 1992, 2(02): 605-618.
[7] 聂士忠.Vondrak数据平滑方法及其在微机上的实现[J].石油大学学报(自然科学版),1994(04):111-114.
[8] 聂士忠.Vondrak数据平滑方法及应用[J].计量技术,2005(07):51-52.
[9] 吴芸芸.Vondrak滤波准则及应用研究[D].中南大学,2012.