本文内容来自学习麻省理工学院公开课:单变量微积分-极限和连续-网易公开课
一、极限
1、 抛出公式:
??????
??????
2、求极限的方法:
from sympy import *
x = symbols('x')
expr = x + 1
limit_expr = limit(expr, x, 0)
limit_expr?

3、给函数出个图:
import matplotlib.pyplot as plt
import numpy as np
from sympy import *
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
x = np.linspace(0,np.pi,50)
y = x + 1
plt.plot(x,y, 'c', label=' fx = x + 1, x >= 0 ')
x = symbols('x')
expr = x + 1
limit_expr = limit(expr, x, 0)
plt.scatter(0, limit_expr, c='r')
x = np.linspace(0,0-np.pi,50)
y = -x + 2
plt.plot(x,y, 'r', label=' fx = -x + 2, x < 0 ')
x = symbols('x')
expr = -x + 2
limit_expr = limit(expr, x, 0)
plt.plot(0,limit_expr,lw=0, marker='o', fillstyle='none')
plt.legend(loc='upper right')
plt.show()?
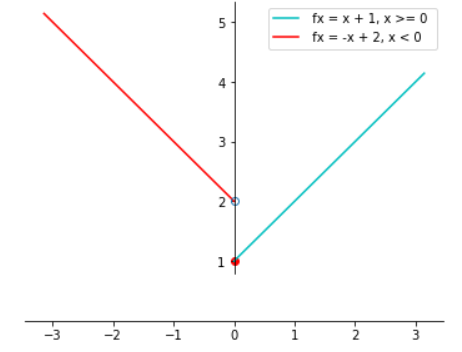
得出的结论是:
二、连续函数和不连续函数
1、函数在点x0连续的条件是:
??? a、 存在, 在x0点的左极限和右极限都存在,同时x0点的左极限等于x0点的右极限
??? b、fx在x0点有定义
??? c、? ( 需要注意的是当计算
, 要避免直接计算
)
2、不连续函数
??? a、跳跃间断,左右两个极限都存在但并不相等,例如上面图显的函数
????????
????????
??? b、可去间断函数,左右两个极限都存在并相等,例如
????????? fx = x / sin(x)
????????? fx = 1- cos(x) / x
import numpy as np
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# plot the functions x / sin(x)
x = np.linspace(-0.1,-2.5,100)
y = x / np.sin(x)
plt.plot(x,y, 'c', label='y= x / sin(x)')
x = np.linspace(0.1,2.5,100)
y = x / np.sin(x)
plt.plot(x,y, 'c')
x,y = symbols('x y')
expr = x/y
z = expr.subs(y,sin(x)).subs(x,0.1)
z1 = expr.subs(y,sin(x)).subs(x,0)
plt.plot(0,z,lw=0, marker='o', fillstyle='none',label=format(z1), color = 'b')
# plot the functions 1-cos(x)/x
x = np.linspace(-0.1,-2.5,100)
y = (1 - np.cos(x)) / x
plt.plot(x,y, 'r', label='y= (1 - cos(x))/x')
x = np.linspace(0.1,2.5,100)
y = (1 - np.cos(x)) / x
plt.plot(x,y, 'r')
x,y = symbols('x y')
expr = y/x
z = expr.subs(y,1 - cos(x)).subs(x,0.1)
z1 = expr.subs(y, 1- cos(x)).subs(x,0)
plt.plot(0,z,lw=0, marker='o', fillstyle='none', color='b')
plt.legend(loc='upper left')
# show the plot
plt.show()?
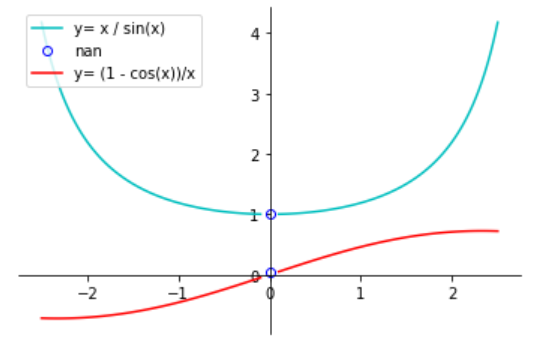
c、无穷间断
????? ,
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
x = np.linspace(-np.pi,-0.1,50)
y = 1 / x
plt.plot(x,y, 'c', label=' fx = 1/x ')
x = np.linspace(0.1,np.pi,50)
y = 1 / x
plt.plot(x,y, 'c')
plt.legend(loc='upper right')
plt.show()?
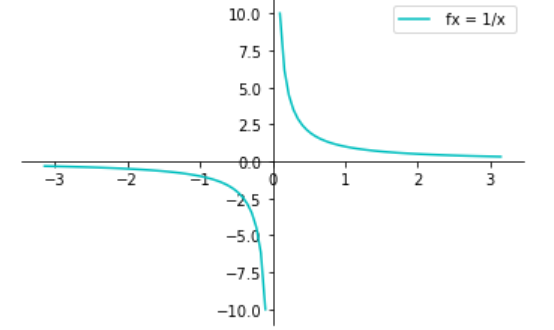
这个函数的导数:
from sympy import *
x = Symbol('x')
f = 1/x
derivative_f = f.diff(x)
derivative_f?
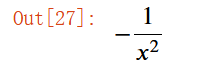
导数的图像:
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
x = np.linspace(-1,-0.1,50)
y = -1 / (x*x)
plt.plot(x,y, 'c', label=' fx = 1/x**2 ')
x = np.linspace(0.1,1,50)
y = -1 / (x*x)
plt.plot(x,y, 'c')
plt.legend(loc='center right')
plt.show()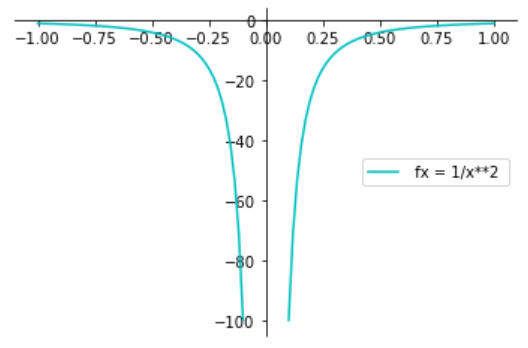
d、其他(丑陋)间断
fx = sin(1/x) 当x趋近于零时,函数值上下反复震荡,但并没有在0点的左极限或右极限
import numpy as np
import sympy
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
x = np.linspace(-1,-0.01,50)
y = np.sin(1/x)
plt.plot(x,y, 'c', label=' fx = 1/x**2 ')
x = np.linspace(0.01,1,50)
y = np.sin(1/x)
plt.plot(x,y, 'c')
plt.legend(loc='center right')
plt.show()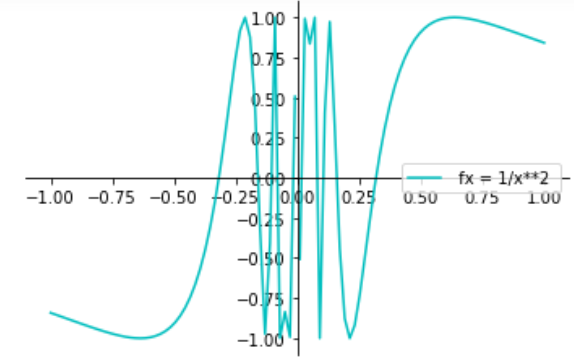
三、定理
当函数f(x)在x0处可导,则这个函数在x0处连续
证明:
当函数在x0处连续的意思就是f(x)在x0处两端的极限有值并几乎等于函数在x0处的值
解:
当x趋近于x0时,
所以有式子? ,而当x趋近于x0时