代码如下:
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
plt.axes(projection='polar')
r = 2
radians = np.arange(0, (2 * np.pi), 0.01)
for theta in radians:
plt.polar(theta, r, '.g')
plt.show()
各个语句的解释:
plt.axes(projection='polar'):将坐标轴投影为极坐标,即在极坐标系下绘图。
r = 2:设定圆形的半径为2。
radians = np.arange(0, (2 * np.pi), 0.01):设置弧度梯度。
plt.polar(theta, r, '.g'):绘制所有符合点的图像。
plt.show():显示图像。
最终得到的图像如下:
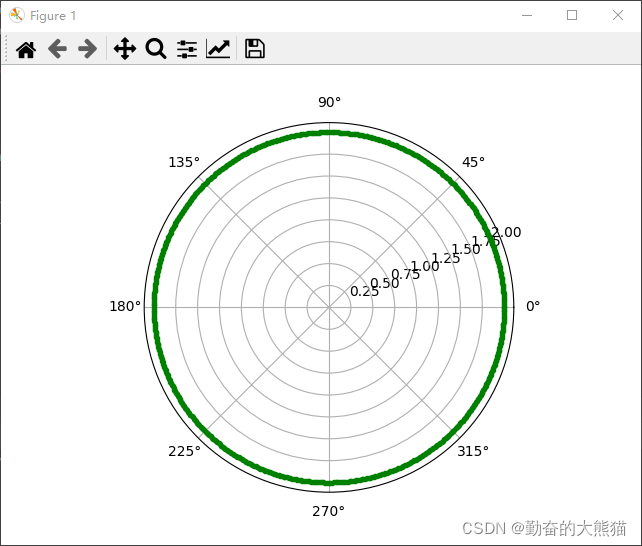
上述语句plt.polar(theta, r, '.g')中的第三个参数'.g'可能大家会比较疑惑。这里该参数的关键字为fmt,是英文单词format的缩写,意为以一个特定的格式向该画图函数中传递参数。并且传递形式为:
fmt = '[marker][line][color]'
但是这里要注意一点,fmt这个关键字需要省略。如果加上就会报错。我们这里的'.g'即表示以绿色点来标记需要绘制的点。最后的附录会给出所有用户可以使用的参数。
注意:plt.polar()该函数事实上绘制的是在极坐标系下的一些离散的点。
之所以我们之前能够绘制一个完整的圆形,在于我们取的弧度值radians值非常密集,很多点绘制在一起,互相重叠形成了圆形的视觉效果,实际上我们绘制的是圆环上的一个个点。为了证明我们的说法,请看下面的代码:
import numpy as np
import matplotlib.pyplot as plt
plt.axes(projection='polar')
r = 2
radians = np.arange(0, (2 * np.pi), 0.1)
for theta in radians:
plt.polar(theta, r, '.g')
plt.show()
最终得到的图像如下:
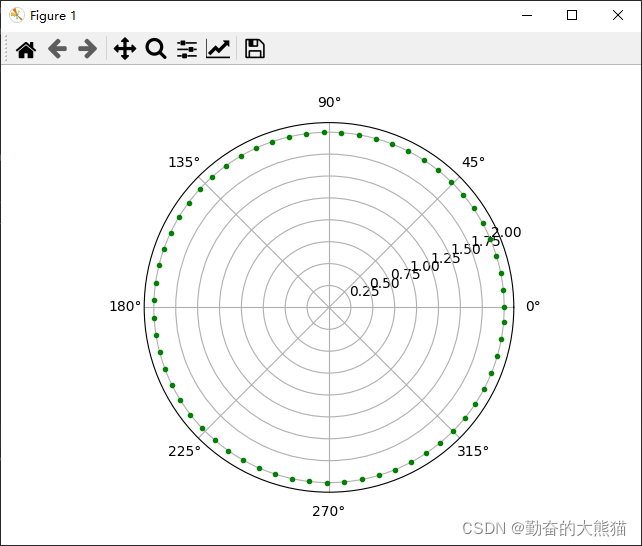
不难发现,当我们降低radians参数值的个数时,我们得到了在圆环上的分开的离散的点。进一步我们可以观察一下,开始我们使用描点绘制圆形图像时,最终得到的图像锯齿比较严重,这是因为我们取得radians参数的个数不足够大,为了使绘制出的圆形更为平滑,我们可以将各个点之间的间隔设置的更小,比如使用如下语句来设定radians值。
radians = np.arange(0, (2 * np.pi), 0.0001)
最终得到的图像如下:
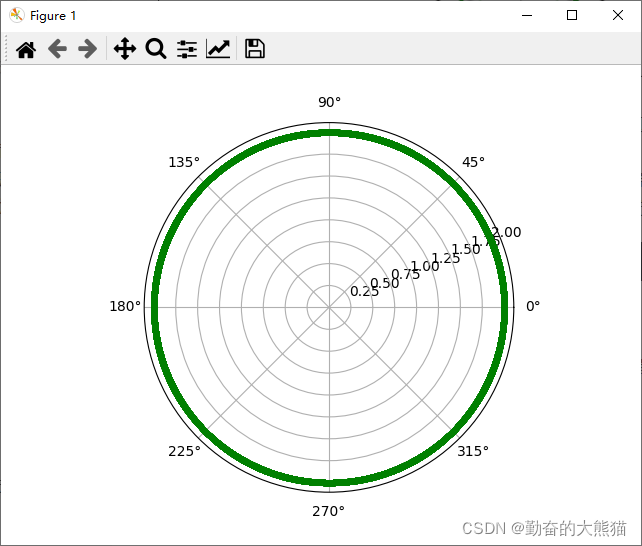
当然,点取的太过密集势必会拖慢我们绘图的速度,所以实际操作时需要自行设定合适的取值。
附录:
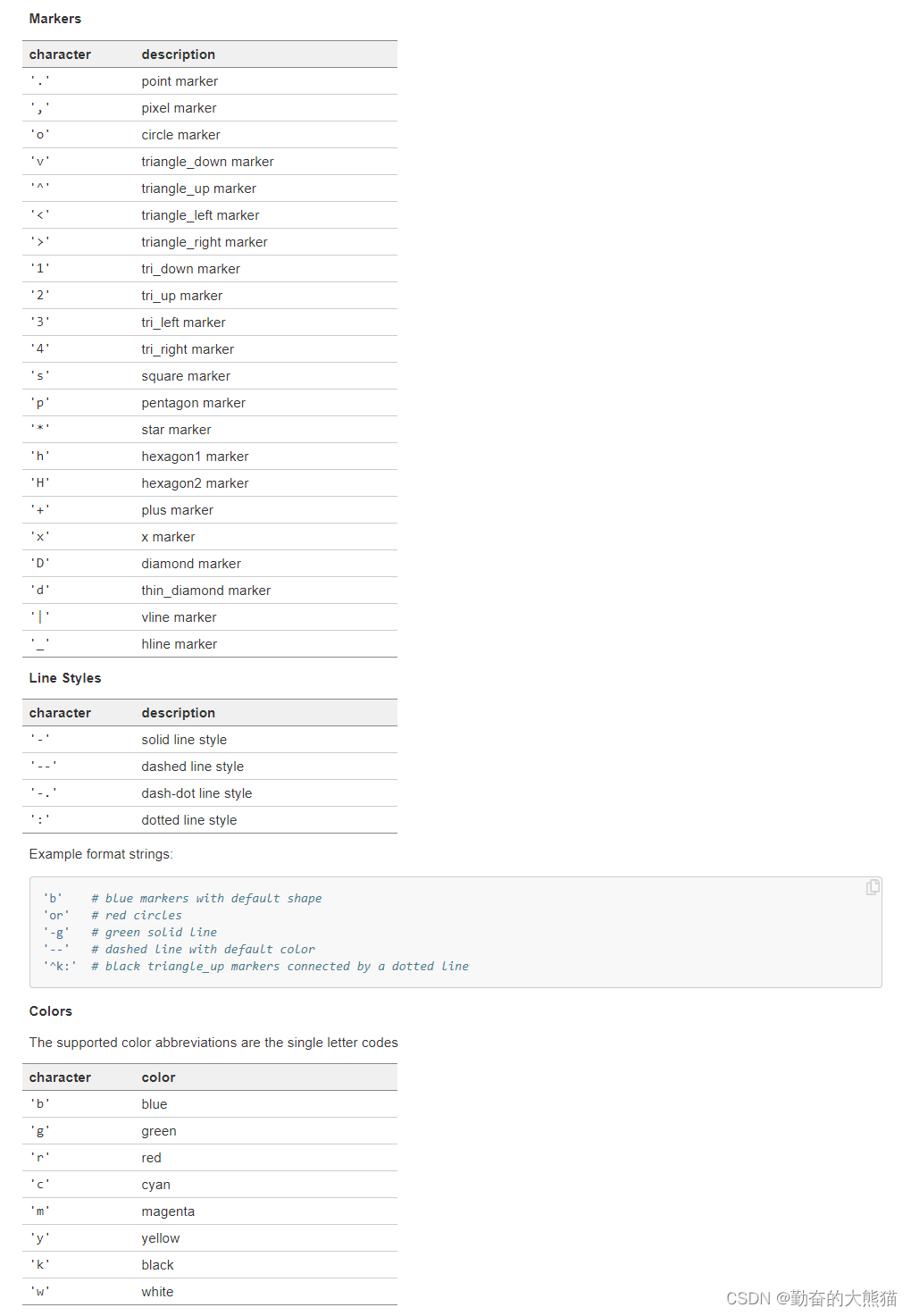
上述图片引用与Matplotlib官网(2021-11-30号版本)(超链接点击跳转)。
码字不易,如果大家觉得有用,请高抬贵手给一个赞让我上推荐让更多的人看到吧~