数学模型与python基础（1）

? 从今天开始码一个数学建模教程，尽管讲数学建模的课程和教材各有各的思路，但是数学建模是利用数学工具分析实际问题，个人认为应当要从如何把一个实际问题变成数学问题开始讲起，所以第一部分先讲一讲数学模型是什么，有什么数学建模的方法，以及python的一些基础知识。

什么是数学模型呢？

就如上文所说，数学建模的问题本质就是把一个实际问题变成一个数学问题，然后用数学工具去解决它的过程。那么从实际问题中抽象出来的数学描述就是数学模型。不同的实际问题当然需要用不同类型的数学语言进行描述，比如微分方程，差分方程，图论，几何，概率图等等。要准备数学建模竞赛，首先应当要对不同的数学描述方法相当熟悉，进而再是结合数学描述，用数学方法解决实际问题。因为要介绍数学模型会相当费篇幅，所以在接下来的几部分里再具体介绍，现在先以微分方程为例，简单地介绍一下。

最近几年，大家被新冠肺炎烦恼得死去活来，在新冠肺炎一开始的时候就有许许多多人开始对新冠肺炎进行建模和预测，通过自己的数学方法来估计这次灾难会什么时候结束。我们现在尝试建立一下最最最简化的传染病模型。

假设一次流行病在一个与世隔绝的小岛上发生，这个小岛上的人无法离开，外部的人也无法进入，而且在感染期间，我们假定出生和死亡对总人口产生的影响忽略不计，一旦传染病发生，这个小岛上的人的结局要么是被感染死亡，要么是被治愈。我们假定这个发生的流行病也不像现在的新冠如此恶毒，可以二次感染，我们认为治愈的人也不会再次感染了，同时这个疾病也没有潜伏期，感染了立即发病。从而我们可以把人群大致分为三类，可以被感染的Susceptible，被感染的Infected，结束感染的Removed（治愈或死亡）。那么接下来，我们要考虑的就是，这三类人群之间的相互转化关系。

直观思考人从未被感染转换为被感染的情况，我们会发现影响因素有这个病毒的传染能力，人与人之间的接触情况等。因为只是单纯举例，因此我们继续简化这个模型，我们认为病毒的传染能力是恒定的，小岛上也没有一个可靠的政府会要求人们戴口罩以及居家隔离，人们也没有半点安全意识，所以接触的情况只与（未被感染的人数×被感染的人数）有关，这个指标标志着全小岛发生未被感染的人和被感染的人接触的可能性，现在我们再乘以一个系数，用以表征发生有效接触的概率以及接触之后感染的概率等等因素，假定为β好了。如果这些被感染的人是不会康复的，但是这个疾病也不致死，那么我们可以列出如下的微分方程。
$\begin{array}{l} \frac{d s}{d t}=-\beta s i \\ \frac{d i}{d t}=\beta s i \end{array}$

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

Population = 10000
i = 1
beta = 0.000002


def diff(x, t):
    s, i = x
    return np.array([-s*i*beta, s*i*beta])


t = np.linspace(0, 1000, 100000)
x = odeint(diff, [Population-1, 1], t)
plt.plot(t, x[:, 0], 'y')
plt.plot(t, x[:, 1], 'b')
plt.grid()
plt.show()

这组数据是瞎给的，没有什么意义，代码在以后的这样的一个代码会生成如下的一张图

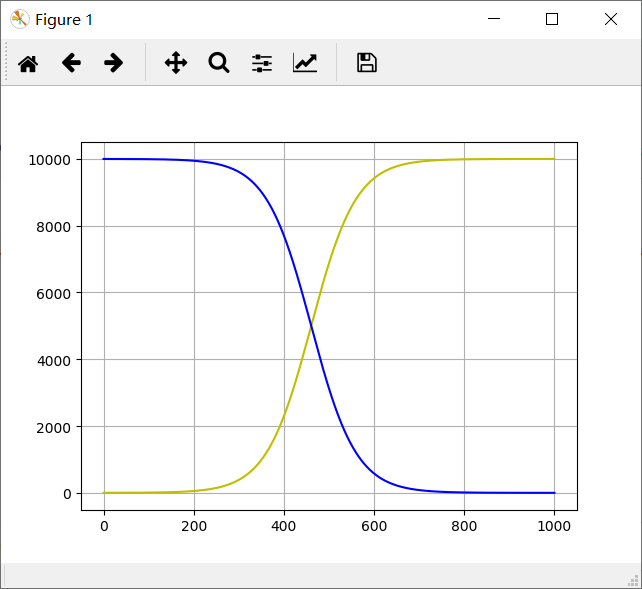
图中的蓝线表示的是未感染人数，逐渐下降，黄线表示的时候已感染人数，逐渐上升。可以看到，上升和下降的速度都呈现了先慢再快最后又变慢的趋势。

现在我们依照同样的思路，假定其中有一部分被感染的人会转变为移出人群，也就是要么治愈要么过世了，很显然移出的情况和治愈能力、致死率以及被感染的人数等因素有关，我们将治愈能力、致死率等因素用一个参数γ表示，则可列出如下方程组。
$\begin{array}{l} \frac{d s}{d t}=-\beta s i \\ \frac{d i}{d t}=\beta s i-\gamma i \\ \frac{d r}{d t}=\gamma i \end{array}$

代码如下

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

Population = 10000
i = 1
beta = 0.000002
gamma = 0.004


def diff(x, t): 
    s, i, r = x
    return np.array([-s*i*beta, s*i*beta-gamma*i, gamma*i])


t = np.linspace(0, 3000, 100000)
x = odeint(diff, [Population-1, 1, 0], t)
plt.plot(t, x[:, 0], 'b')
plt.plot(t, x[:, 1], 'y')
plt.plot(t, x[:, 2], 'r')
plt.grid()
plt.show()

参数同样是瞎给的，会得到下面这样一张图

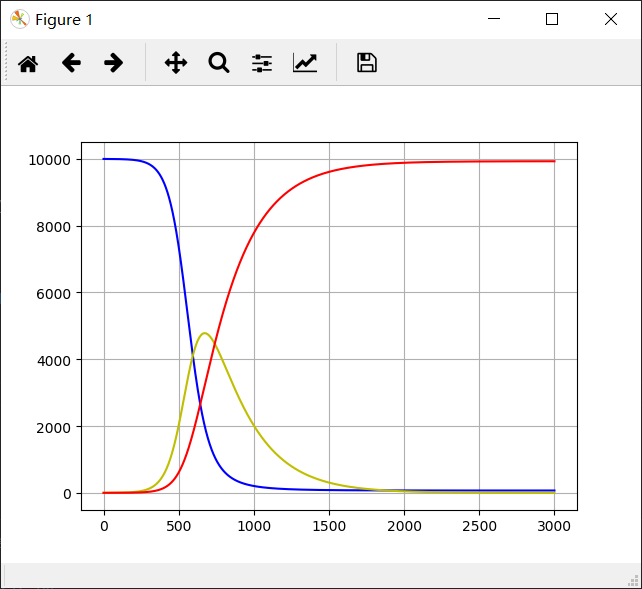
可以看出，最后所有人都被移出了，中间有一段时间，被感染的人达到过很高的水平，但是很快也就降下来了。

这个就是传染病学中的SIR模型。我们从一开始用指标表达人口，表达不同类别的人群，表达不同类别的人群之间的转换关系，然后就完成了一个非常简单的数学模型的构建。但是这个数学模型还是和真实情况相差甚远，潜伏期没有考虑，人口流动没有考虑，隔离等措施对于β和γ的影响没有考虑……当我们把越来越多复杂的参数考虑进去，我们的数学模型就越来越贴近实际情况了，但是本质的思路和我们刚才所做的是非常类似的。

我们刚刚的参数都是瞎给的，那么实际数学建模中呢？实际的数学建模中，参数可以根据我们构建数学模型的原理去计算获得，比如我们知道一个国家一个地区的人口，那么人口就可以直接给，如果我们知道一个传染病的传染能力特性，那么传染病的β和γ也可以直接给，这就是为什么在做数学建模竞赛的时候，常常需要查阅大量资料和论文。当然也有很多情况下，这些参数没那么容易知道，我们可以基于数据，通过回归之类的手段去获取参数，这个内容以后再说。

第一篇就到此为止，以后的内容会结合python如何处理数据以及不同实际问题如何抽象成数学模型，数学模型又如何通过数学工具来解决问题逐步展开。