美式期权定价方法之最小二乘蒙特卡洛模拟
前言
前文对欧式期权的蒙特卡洛模拟定价方法进行了介绍和python量化,本章节主要是对前一章节的补充。也就是介绍美式期权的蒙特卡洛定价方法。
一、美式期权
不同于欧式期权,美式期权合约的行权时间是不固定的。
美式期权(American option)是指可以在成交后有效期内任何一天被执行的期权。也就是指期权持有者可以在期权到期日以前的任何一个工作日,选择执行或不执行期权合约。
美式期权允许期权持有者在到期日或到期日前执行购买(如果是看涨期权)或出售(如果是看跌期权)标的资产的权利。
二、LSM定价方法
蒙特卡洛模拟作为灵活而有力的数值方法,其本身不适合解决美式期权或者百慕大期权的定价问题。学者Longstaff和Schwarta提出了最小二乘蒙特卡洛模拟方法(Least-Squares Monte Carlo,LSM),成为了美式期权定价的经典方法。
下面对LSM方法进行python实现,代码如下:
# 美式期权定价(最小二乘蒙特卡洛模拟法,LSM)
S0=100
r=0.05
sigma=0.25
T=1
I=50000
M=50
def gmb_mcs_amer(K,option='call'):
dt=T/M
df=math.exp(-r*dt)
S=np.zeros((M+1,I))
S[0]=S0
sn=gen_sn(M,I)
for t in range(1,M+1):
S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+sigma*math.sqrt(dt)*sn[t])
if option=='call':
h=np.maximum(S-K,0)
else:
h=np.maximum(K-S,0)
V=np.copy(h)
for t in range(M-1,0,-1):
reg=np.polyfit(S[t],V[t-1]*dt,7)
C=np.polyval(reg,S[t])
V[t]=np.where(C>h[t],V[t+1]*df,h[t])
C0=df*np.mean(V[1])
return C0
调用函数,假设期权行权价为110,则看涨期权和看跌期权价格为:
gmb_mcs_amer(100,option='call')
1.4620120629034186
gmb_mcs_amer(110,option='put')
9.918961211536654
三、美式期权与欧式期权定价对比
这一章会用到欧式期权蒙特卡洛模拟方法,代码如下,也可以看本栏目的第二篇文章。
def gbm_mcs_dyna(K,option='call'):
dt=T/M
S=np.zeros((M+1,I))
S[0]=S0
sn=gen_sn(M,I)
for t in range(1,M+1):
S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+sigma*math.sqrt(dt)*sn[t])
if option=='call':
hT=np.maximum(S[-1]-K,0)
else:
hT=np.maximum(K-S[-1],0)
C0=math.exp(-r*T)*np.mean(hT)
return C0
对不同行权价的期权数据进行计算,并且对比欧式期权和美式期权的价格差。
看涨期权
euro_res=[]
amer_res=[]
S0=100
r=0.05
sigma=0.25
T=1
I=50000
M=50
k_list=np.arange(80.,110.1,2.)
for K in k_list:
euro_res.append(gbm_mcs_dyna(K,option='call'))
amer_res.append(gmb_mcs_amer(K,option='call'))
euro_res=np.array(euro_res)
amer_res=np.array(amer_res)
fig,(ax1,ax2)=plt.subplots(2,1,sharex=True,figsize=(10,6))
ax1.plot(k_list,euro_res,'b',label='european call')
ax1.plot(k_list,amer_res,'ro',label='american call')
ax1.set_ylabel('call option value')
ax1.legend()
wi=1.0
ax2.bar(k_list-wi/2,(amer_res-euro_res)/euro_res*100,wi)
ax2.set_xlabel('strike')
ax2.set_ylabel('early exercise premium in %')
ax2.set_xlim(left=75,right=125)
看跌期权
```bash
euro_res1=[]
amer_res1=[]
S0=100
r=0.05
sigma=0.25
T=1
I=50000
M=50
k_list=np.arange(80.,110.1,2.)
for K in k_list:
euro_res1.append(gbm_mcs_dyna(K,option='put'))
amer_res1.append(gmb_mcs_amer(K,option='put'))
euro_res1=np.array(euro_res1)
amer_res1=np.array(amer_res1)
fig,(ax1,ax2)=plt.subplots(2,1,sharex=True,figsize=(10,6))
ax1.plot(k_list,euro_res1,'b',label='european put')
ax1.plot(k_list,amer_res1,'ro',label='american put')
ax1.set_ylabel('put option value')
ax1.legend()
wi=1.0
ax2.bar(k_list-wi/2,(amer_res-euro_res)/euro_res*100,wi)
ax2.set_xlabel('strike')
ax2.set_ylabel('early exercise premium in %')
ax2.set_xlim(left=75,right=125)
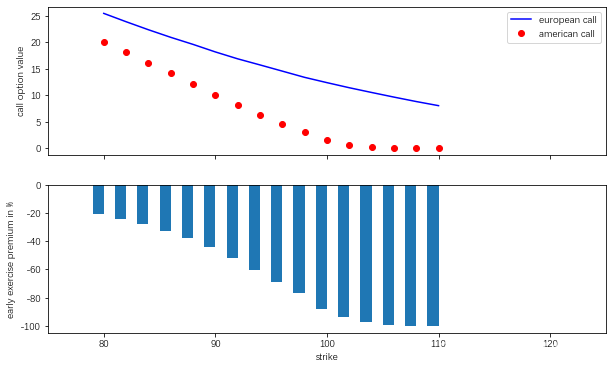
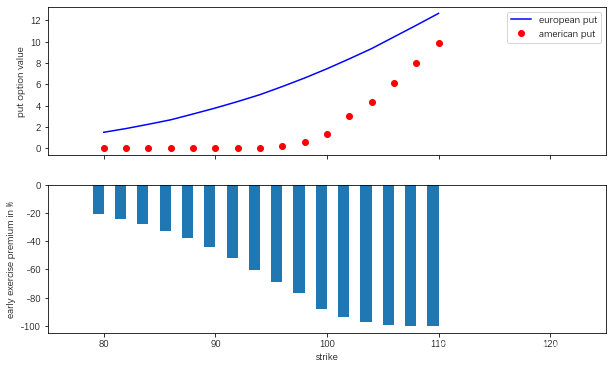
从图中可以看出,美式期权的价格处于欧式期权的下界,两者价格的差值通常称为提前行权溢价。
总结
本章对美式期权的蒙特卡洛模拟解法进行了介绍。