引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。
本系列文章首发于微信公众号：JavaNLP

关注公众号

本文对逻辑回归的原理进行简单的介绍，包含公式推导。逻辑回归是可以作为分类任务的基准，也是神经网络的基石。一个神经网络可以看成是一系列的逻辑回归组成。所以掌握逻辑回归就相当重要。

回归与分类

我们前面学习的线性回归属于回归问题，今天介绍的逻辑回归属于分类问题。

回归：预测一个连续值；

分类：预测一个离散值；

逻辑回归虽然名字中包含回归，实际上处理的是分类问题，为啥名字这么奇怪呢，有历史原因，这里就不深究了。

逻辑回归用于处理二分类问题，所谓二分类问题，就是分类的类别只有两个的问题。比如判断邮件是否为垃圾、情绪分析中的情绪是正向的还是负向的等。

那么逻辑回归是如何处理二分类问题的呢？答案就是通过Sigmoid函数。

机器学习分类器的核心组件

逻辑回归是一种基于监督学习的分类器。机器学习分类器需要一个训练集，包含 $m$ 个输入/输出对 $x^{(i)},y^{(i)})$ 。一个分类机器学习系统有四个组件：

输入的特征表示对于每个输入样本 $x^{(i)}$ ，可以表示为特征向量 $[x_1,x_2,\cdots,x_n]$ ， $x^{(j)}_i$ 表示输入 $x^{(j)}$ 的第 $i$ 个特征，有时简记为 $x_i$
计算估计类别 $\hat y$ 的分类函数，通过 $p (y ∣ x)$
一个学习的目标函数，通过计算训练样本上的最小化误差
一个优化目标函数的算法，常用的是随机梯度下降法

Sigmoid函数

我们先来看下输入的表示，通常我们有很多个输入样本。对于第 $i$ 个样本 $x^{(i)}$ ，可以表示为特征向量 $[x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)}]$ ，这里假设有 $n$ ?个特征。

考虑一个输入样本 $x$ ，表示为特征向量 $[x_1,x_2,\cdots,x_n]$ ，输出 $y$ 可能是 $1$ 或 $0$ ，其中 $1$ 表示属于某个类别的话，那么 $0$ 就表示不属于那个类别。

逻辑回归从一个训练集中学习权重向量和一个偏置。每个权重 $w_i$ 与输入样本中的一个特征 $x_i$ 绑定，最后加上偏置项 $b$ 。权重和偏置项都是实数。

为了判断类别，首先让每个特征乘上对应的权重，然后加上 $b$ ，得到一个实数 $z$ ，表示属于该类别的依据。
$\left( \sum_{i=1}^n w_ix_i \right) + b \tag{1}$
实数 $z$ 越大，表示该特征对属于该类别的贡献度越大。我们也可以通过线性代数中的点乘的方式来简化这个公式：
$\cdot x + b \tag{2}$
但是，这样得到的 $z$ 显然不是一个概率值，如果细心的童鞋可能回发现，这不就是线性回归的公式吗。没错，但是逻辑回归需要利用一个函数来把一个属于 $-\infty$ 到 $+\infty$ 的实数值转换为 $[0, 1]$ 之间的概率值。

这个函数就是Sigmoid函数，记为 $\sigma$ ，也称为逻辑函数。

它的公式如下：
$\sigma(z) = \frac{1}{1 + e^{-z}} = \frac{1}{1 + \exp(-z)} \tag{3}$

它的函数图像如下：

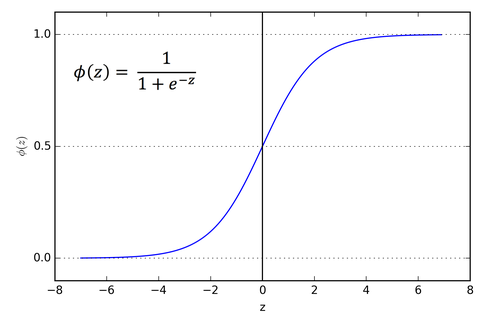
Sigmoid函数的优点是：它可以将任意实数压缩到 $[0, 1]$ 之间，这刚好符合概率的定义。同时它是可导的。

为了让Sigmoid函数的输出刚好是一个概率，我们要确保 $P (y = 1) + P (y = 0) = 1$ 。我们来看是否具有这种性质：
$\begin{aligned} P(y=1) &= \sigma(w \cdot x + b) \\ &= \frac{1}{1 + \exp(-(w\cdot x +b))} \\ P(y=0) &= 1 - \sigma(w \cdot x +b)\\ &= 1 - \frac{1}{1 + \exp(-(w\cdot x + b))} \\ &= \frac{\exp(-(w \cdot x + b))}{1 + \exp(-(w\cdot x + b))} \\ &= \frac{1}{1 + \exp(w \cdot x + b)} \\ &= \sigma(-(w \cdot x +b)) \end{aligned} \tag{4}$
也就是说，Sigmoid函数还有以下性质：
$\sigma(x) = \sigma(-x) \tag{5}$
所以有 $P(y=0)=\sigma(-(w\cdot x + b))$ 。

决策边界

给定输入 $x$ ，我们已经知道了如何取计算属于类别 $y$ 的概率 $P (y = 1 ∣ x)$ 。

但我们如何判断 $x$ 是否属于类别 $y$ 呢？直观地，如果概率 $P (y = 1 ∣ x) > 0.5$ ，我们就说它属于该类别，否则不属于该类别。那么 $0.5$ 就是决策边界。
$\text{decision}(x)= \begin{cases} 1, & \text {if $P(y=1|x) > 0.5$}\\ 0, & \text{otherwise} \end{cases} \tag{6}$

逻辑回归中的损失函数

我们知道每个样本 $x$ 对应的正确标签 $y$ 。根据公式 $(4)$ 计算的是对真实 $y$ 的估计 $\hat y$ ，我们想让估计 $\hat y$ 和真实 $y$ 越接近越好。这里的“接近”衡量的是距离，我们称这种距离为损失(loss)或者代价(cost)。计算损失或代价的函数为损失函数或代价函数。

给定样本 $x$ ，我们需要一个损失函数来衡量类器的输出( $\hat y= \sigma(w \cdot x + b)$ )与真实输出 $y (0 或 1)$ 有多近。可以记为：
$L(\hat y, y) = \hat y\text{与真实}y\text{有多不同} \tag{7}$
该函数倾向于模型更可能将训练样本分类成正确的类别。这称为条件最大似然估计：我们选择参数 $w, b$ 来最大化训练数据中给定样本 $x$ 属于真实标签 $y$ 的对数概率。此时对应的损失函数为负对数似然损失，通常称为交叉熵损失。

对于单个样本 $x$ ，我们希望学到权重能最大化正确类别概率 $p (y ∣ x)$ 。由于只有两个离散的输出(0或1)，这是一个伯努利分布，我们可以将分类器为一个样本产生的概率 $p (y ∣ x)$ 表示为如下：
$\hat y ^y(1 -\hat y)^{1-y} \tag{8}$
如果正确类别 $y = 1$ ，那么上式右边简化为 $\hat y$ ；如果 $y = 0$ ，那么简化为 $\hat y$ 。

我们把等式两端取对数，取对数并不会改变单调性：
$\begin{aligned} \log p(y|x) &= \log {[ \hat y ^y(1-\hat y)^{1-y}]} \\ &= y \log \hat y + (1-y) \log (1 -\hat y) \end{aligned} \tag{9}$
上式描述了一个应该最大化的对数似然。为了让它变成损失函数，我们增加一个负号，变成了交叉熵损失 $L_{CE}$ (loss of cross entropy):
$L_{CE}(\hat y,y) = - \log p(y|x) = - [y\log \hat y + (1-y)\log (1 - \hat y)] \tag{10}$
最终，我们代入 $\hat y =\sigma(w \cdot x + b)$ :
$L_{CE}(\hat y,y) = - [y\log \sigma(w \cdot x + b) + (1-y)\log (1 - \sigma(w \cdot x + b))] \tag{11}$
为什么最小化这个负对数似然就能实现我们想要的结果？一个完美的分类器会将正确的输出标记为1，错误的输出标记为0。意味着，如果 $y = 1$ ，输出 $\hat y$ 越高，分类器越好，输出的 $\hat y$ 越低，分类器越差；如果 $y = 0$ ， $1-\hat y$ 越大，分类器越好。

$\hat y$ 的负对数(真实 $y = 1$ )或 $\hat y$ 的负对数(真实 $y = 0$ ?)是一个方便的损失指标，因为它可以是从0( $-\log 1 =0$ ，代表没有损失)到无穷大( $\log 0 = \infty$ ?)。该损失函数也确保正确答案的概率最大化，错误答案的概率最小化；由于它们之和等于1，正确答案概率的任何增加都是以减少错误答案为代价的。

梯度下降

使用梯度下降的目的是找到最优的权重：最小化损失函数。在下面的公式中，我们看到损失函数 $L$ 由权重参数化的，我们将在机器学习中将其称为 $\theta$ （在逻辑回归中 $\theta = w,b$ ）。所以目标是找到权重集能最小化损失函数，平均所有的样本就是：
$\hat \theta = \arg \min_{\theta} \frac{1}{m} \sum_{i=1}^m L_{CE} (f(x^{(i)};\theta),y^{(i)}) \tag{12}$
我们如何找到这个损失函数的最小值呢？梯度下降是一种方法，通过计算函数的斜率向哪个方向（在参数θ的空间）上升得最陡峭，并朝着相反的方向移动来找到函数的最小值。

对于逻辑回归，损失函数是一个凸函数，即只有一个最小值，所以梯度下降能保证从任意点都能达到最小值。而多层神经网络的损失函数时非凸的，可能受困于局部极小值。

在一个真实的逻辑回归中，参数向量 $w$ 的元素个数可能很多，即每个特征 $x_i$ 都有对应的权重 $w_i$ 。对于 $w$ 中的每个维度/变量 $w_i$ (加上偏置 $b$ )，梯度将告诉我们该变量的斜率的部分。在每个维度 $w_i$ ，我们描述斜率为损失函数的偏导 $\frac{\partial}{\partial w}$ 。本质上我们想知道：在变量 $w_i$ 上的一个小改变会影响总损失函数 $L$ 多少？

因此，在形式上，多变量函数 $f$ 的梯度是一个向量，其中每个元素都表示 $f$ 相对于对应变量的偏导。我们将使用 $\nabla$ 来指梯度，并将 $\hat y$ 表示为 $f(x;\theta)$ :

$\nabla L(f(x;\theta),y) = \begin{bmatrix} \frac{\partial}{\partial w_1}L(f(x;\theta),y) \\ \frac{\partial}{\partial w_2}L(f(x;\theta),y) \\ \vdots\\ \frac{\partial}{\partial w_n}L(f(x;\theta),y) \\ \frac{\partial}{\partial b}L(f(x;\theta),y) \end{bmatrix} \tag{13}$
基于梯度更新参数 $\theta$ 的式子为：
$\theta_{t+1} = \theta_t - \eta \nabla L(f(x;\theta),y) \tag{14}$

逻辑回归的梯度

为了更新参数 $\theta$ ，我们需要梯度 $\nabla L(f(x;\theta),y)$ ?的定义，我们知道逻辑回归的交叉熵损失函数为：
$L_{CE}(\hat y,y) = - [y\log \sigma(w \cdot x + b) + (1-y)\log (1 - \sigma(w \cdot x + b))]$

要求上式对某个参数的导数，我们回顾一下：
$(\log x)^\prime = \frac{1}{x} \\ (\frac{u}{v})^\prime = \frac{u^\prime v - u v^\prime}{v^2}$

我们知道， $\sigma(z) = \frac{1}{1+ e^{-z}}$ 。我们先计算 $\frac{\partial \sigma(z)}{\partial z}$ ，令 $u=1,v=1+e^{-z}$ :

$\begin{aligned} \frac{\partial \sigma(z)}{\partial z} &= (\frac{1}{1 + e^{-z}})^\prime \\ &= \frac{0 \times (1+e^{-z}) - 1\times (1+e^{-z})^\prime}{(1 + e^{-z})^2} \\ &= \frac{- (-e^{-z})}{(1+e^{-z})^2} \\ &= \frac{1 + e^{-z} - 1}{(1+e^{-z})^2} \\ &= \frac{1}{1 + e^{-z}} - \frac{1}{(1 + e^{-z})^2} \\ &= \frac{1}{1 + e^{-z}} \left( 1 - \frac{1}{1 + e^{-z}} \right) \\ &= \sigma(z)(1 - \sigma(z)) \end{aligned}$

我们计算损失函数对某个权重 $w_j$ 的梯度：

$\begin{aligned} \frac{\partial L_{CE}}{\partial w_j} &=\frac{\partial }{\partial w_j} - [y\log \sigma(w \cdot x + b) + (1-y)\log (1 - \sigma(w \cdot x + b))] \\ &= -\left [ \frac{\partial }{\partial w_j}y\log \sigma(w \cdot x + b) + \frac{\partial }{\partial w_j} (1-y)\log (1 - \sigma(w \cdot x + b)) \right] \\ &= - \frac{y}{\sigma(w \cdot x + b) }\frac{\partial}{w_j}\sigma(w \cdot x + b) - \frac{1-y}{1 - \sigma(w \cdot x + b) }\frac{\partial}{w_j}(1 - \sigma(w \cdot x + b) ) \\ &= - \frac{y}{\sigma(w \cdot x + b) }\frac{\partial}{w_j}\sigma(w \cdot x + b) - \frac{1-y}{1 - \sigma(w \cdot x + b) }\frac{\partial}{w_j}-\sigma(w \cdot x + b) \\ &= \left[ \frac{1-y}{1 - \sigma(w \cdot x + b) } - \frac{y}{\sigma(w \cdot x + b) }\right]\frac{\partial}{w_j}\sigma(w \cdot x + b) \\ &= \left[\frac{\sigma(w \cdot x + b)(1-y) - y[1 - \sigma(w \cdot x + b) ]}{\sigma(w \cdot x + b)[1 - \sigma(w \cdot x + b)]} \right]\frac{\partial}{w_j}\sigma(w \cdot x + b) \\ &= \left[\frac{\sigma(w \cdot x + b) - y}{\sigma(w \cdot x + b)[1 - \sigma(w \cdot x + b)]} \right]\frac{\partial}{w_j}\sigma(w \cdot x + b) \\ &= \left[\frac{\sigma(w \cdot x + b) - y}{\sigma(w \cdot x + b)[1 - \sigma(w \cdot x + b)]} \right]\sigma(w \cdot x + b)[1-\sigma(w \cdot x + b)]\frac{\partial (w\cdot x + b)}{\partial w_j}\\ &= \left[\frac{\sigma(w \cdot x + b) - y}{\sigma(w \cdot x + b)[1 - \sigma(w \cdot x + b)]} \right]\sigma(w \cdot x + b)[1-\sigma(w \cdot x + b)]x_j \\ &= [\sigma(w \cdot x + b) - y]x_j \\ &= (\hat y - y)x_j \end{aligned} \tag{15}$
最后得到的结果很简单，描述的就是预测值减去真实值乘上对应的输出。