本文内容来自于学习麻省理工学院公开课:单变量微积分-微分方程和分离变量-网易公开课
一、微分方程:
1、第一类
2、第二类
湮没算符
?(当y=0时, 可以看到等式成立 ( )
这里老师说这个是正态分布的公式
检查:
正态分布曲线公式:
(μ是遵从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差)
正态分布标准差的意义在于,它遵循一个经验法则,即大约95%的测量值落在均值附近的+/- 2倍个标准差之间
标准差的计算公式:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_aspect(1 )
def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
yarr = []
xarr = np.linspace(xFrom ,xTo, steps)
for xval in xarr:
yval = expr.subs(x,xval)
yarr.append(yval)
y_nparr = np.array(yarr)
plt.plot(xarr, y_nparr, c=color, label=label)
def TangentLine(exprY,x0Val,xVal):
diffExpr = diff(exprY)
x1,y1,xo,yo = symbols('x1 y1 xo yo')
expr = (y1-yo)/(x1-xo) - diffExpr.subs(x,x0Val)
eq = expr.subs(xo,x0Val).subs(x1,xVal).subs(yo,exprY.subs(x,x0Val))
eq1 = Eq(eq,0)
solveY = solve(eq1)
return xVal,solveY
def DrawTangentLine(exprY, x0Val,xVal1, xVal2, clr, txt):
x1,y1 = TangentLine(exprY, x0Val, xVal1)
x2,y2 = TangentLine(exprY, x0Val, xVal2)
plt.plot([x1,x2],[y1,y2], color = clr, label=txt)
def Newton(expr, x0):
ret = x0 - expr.subs(x, x0)/ expr.diff().subs(x,x0)
return ret
x = symbols('x')
a =3
m = 0.9
expr = (1/(2*np.pi*a)**(0.5)) * np.e**(-(x-m)**2/2*(a**2))
DrawXY(-1,3,100,expr,'blue','',plt)
#plt.legend(loc='lower right')
plt.show()
?
标准正态分布曲线
?
expr = (1/(2*np.pi)**(0.5)) * np.e**(-(x)**2/2)
DrawXY(-3,3,100,expr,'blue','',plt)
#plt.legend(loc='lower right')
plt.show()
?
本节老师给出的方程:
?
A =3
expr = A * np.e**(-(x)**2/2)
DrawXY(-3,3,100,expr,'blue','',plt)
#plt.legend(loc='lower right')
plt.show()
?
二、分离变量法
?微分方程可化为
三、解微分方程举例
A = 3
四、例题
1、由(0,0)点引一条直线落在函数y的曲线上,交点处曲线y的斜率是这条直线的斜率的2倍,求这条曲线的方程
检查
注意: 在这个式子中,x=0处的值是没定义的
从几何上看, x=0时曲线的切线是平行于x轴的,而从(0,0)点引出的直线也落在(0,0)点
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_aspect(1)
A = 4
expr = A * x**2
DrawXY(-3,3,100,expr,'blue','A * x**2',plt)
A =-4
expr = A * x**2
DrawXY(-3,3,100,expr,'blue','-A * x**2',plt)
plt.legend(loc='lower right')
plt.show()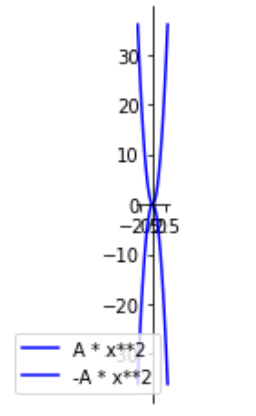
?
2、上题中的抛物线与曲线相交处,处处垂直,求这条曲线的方程
(两直线垂直,在两者斜率都存在的前提下,其斜率的乘积为-1;如果其中直线不存在斜率,则另一条直线斜率为0。对于两条互相垂直的直线而言,它们的斜率互为倒数,因此其斜率的乘积为-1)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_aspect(0.2)
A = 4
expr = A * x**2
DrawXY(-3,3,100,expr,'blue','A * x**2',plt)
A =-4
expr = A * x**2
DrawXY(-3,3,100,expr,'blue','-A * x**2',plt)
plt.legend(loc='lower right')
A = 5
expr = abs(A - 0.5*x**2)**0.5
DrawXY(-3,3,100,expr,'blue','|(A - 0.5*x**2)**0.5|',plt)
expr = 0 - abs(A - 0.5*x**2)**0.5
DrawXY(-3,3,100,expr,'blue','-|(A - 0.5*x**2)**0.5|',plt)
plt.show()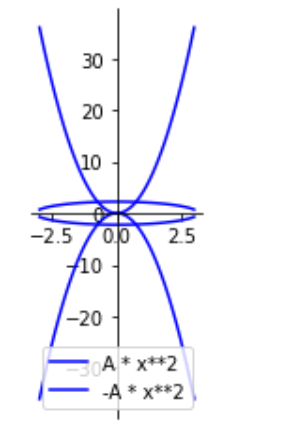
这个曲线在y=0处没有意义(它的斜率y在分母),所以它是椭圆的上半或下半部分
最后老师说了一下这门课的目标
即通过一个函数的导数,有时还需要通过它的二阶导数的信息得到函数本身的信息。
?