蓝桥杯python组第2021届第三题
第三题 题目大意
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有n箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆L、W、H的货物,满足n=L×W×H。
给定n,请问有多少种堆放货物的方案满足要求。
例如,当n=4时,有以下6种方案:1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
请问,当n=2021041820210418(注意有16位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
总体思路
根据所给的小例子,我们可以知道就是通过寻找L、W、H使得乘积等于n。我们可以通过循环套嵌循环来实现,但也要考虑循环的次数。
思路一
在考虑循环的次数时,我们考虑让每一个循环循环n次,n/2次,以及(根号n)次,所得的结果是一样的,但是效率上来看,当然循环的越少,效率越高。通过获得n的公因数,来求得L、W、H。下面介绍(根号n)次的计算方法:
n = 2021041820210418
#n = 4
i = 1
#print(n%3)
res = [] # 构建一个列表,用于n的公因数。
while i*i<=n: # 当i小于等于(根号n)时
if i*i<n:
if n%i==0: # 判断n除以i能够整除时
res.append(i) # 分别将i和n/i添加到公因数中
res.append(int(n/i))
i+=1
else: # 当i*i等于n时,添加i即可
res.append(i)
i+=1
print(res)
plans = []
# 构建三个循环,分别使得L、W、H在公因数中循环,使得乘积为n
for L in res:
for W in res:
if L*W>n:
continue
for H in res:
if L*W*H == n:
plans.append((L,W,H))
#print(plans)
print("输出结果为:",len(plans))
# 输出结果为: 2430
由于本题是填空题,算出结果即可。但是在编程中,它会显示超出时间限制。究其原因,是在计算公因数时超时了。尽管我们已经让循环缩减到(根号n)次,但是依然超出时间。因此我们考虑另一种思路。
思路二
采用深度优先搜索的算法进行。我们知道任何一个数都可以分解为其质因子的乘积。为了提高效率,我们可以先算出来n的所有质因子,再由这些质因子相互组合,便可以得到所有的L、W、H。
求解所有质因子代码:
n = 2021041820210418
res=[]
while True:
# 先将所有质因子中2、3的质数都提取出来
if n%2==0:
res.append(2)
n /= 2
continue # 继续while True下的循环
if n%3==0:
res.append(3)
n /= 3
continue
# 上述两个判断的好处是能够线把所有的2、3质因子提取出来。
for i in range(1,int(n**0.5//6+2)):
# 为了能够循环,比如n为35时,(根号n)为5点...,再除以6取整后为0,
# 为至少能够循环一次故+2
i_1 = 6*i-1 # 除2、3外的质数均为6的整数倍±1(可自行推导)
i_2 = 6*i+1
if n%i_1==0: # 表示6*i-1为n的质因子
res.append(i_1)
n /= i_1
if n%i_2==0: # 表示6*i+1为n的质因子
res.append(i_2)
n /= i_2
if n==1: #由于前面都是找到n的质因子便除以该因子,因此此处判断是否n==1
break
if n==1: # 此处相同
break
print(res)
# [2, 3, 3, 3, 17, 131, 2857, 5882353]
此时我们便能够得到n的所有质因子。接下来我们需要考虑的问题就是如何将这些质因子进行组合,以便能够不漏一个的统计除所有的L、W、H。借助于深度搜索的想法。我的想法是,设计3个容器,分别为Ltank,Wtank,Htank,将上述求得的质因子分别放到这几个容器中相乘即可。代码如下:
# 借助于深度优先搜索的思路来计算。
Ltank = 1
Wtank = 1
Htank = 1
row = 0
catch = set() # 以防出现重复的情况,我们这里设计的集合的形式。
def DFS(row,Ltank,Wtank,Htank):
if row == len(res): # 判断是否将质因子都用了
catch.add((Ltank,Wtank,Htank))
return
Ltank *= res[row]
DFS(row+1,Ltank,Wtank,Htank)
Ltank /= res[row]
Wtank *= res[row]
DFS(row + 1, Ltank, Wtank, Htank)
Wtank /= res[row]
Htank *= res[row]
DFS(row + 1, Ltank, Wtank, Htank)
Htank /= res[row]
DFS(0,Ltank,Wtank,Htank)
print(len(catch))
# 将上述两个代码连起来运行即可得到
# 2430
为了更好地解释DFS函数,我利用表格的形式,以一个简单的例子来进行说明,大家可以在pycharm中进行debug,观察。
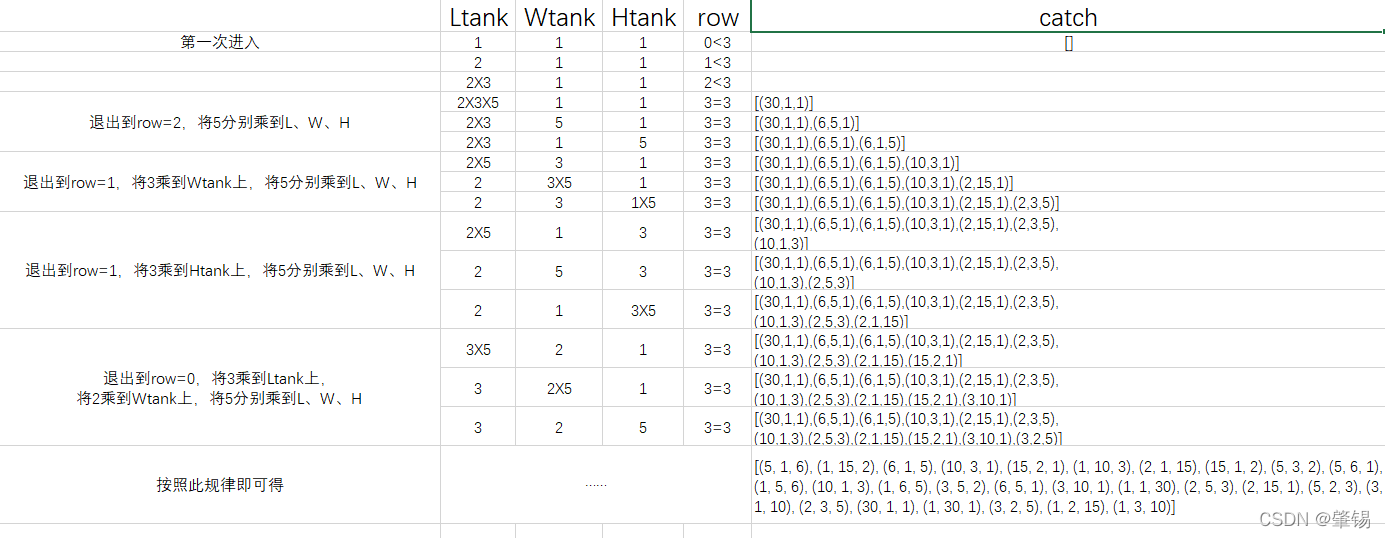
我们进行进一步思考:我们将每一个质因子放到Ltank、Wtank、Htank三个容器中都是等可能的,那么总可能性就是(3**质因子个数)。比如质因子的个数为3,总可能性就是27。
因此我们做了以下实验:
| n | 质因子 | 可能性 | 乘积 |
|---|---|---|---|
| 210 | [2, 3, 5, 7] | 81 | 3X3X3X3 |
| 90 | [2, 3, 3, 5] | 54 | 3X6X3 |
| 270 | [2, 3, 3, 3, 5] | 90 | 3X10X3 |
| 810 | [2, 3, 3, 3, 3, 5] | 135 | 3X15X3 |
我们发现当质因子互不相同的时候,总可能性就是(3**质因子个数)。
当质因数有相同的时候
| 相同的个数 | 可能性 |
|---|---|
| 2 | 6=3+2+1 |
| 3 | 10=4+3+2+1 |
| 4 | 15=5+4+3+2+1 |
这里用到的应该是概率论里边的知识,如果有朋友能够解释清楚,欢迎在下方评论~
返回来我们再看题目中的n=2021041820210418
此时质因子为:[2, 3, 3, 3, 17, 131, 2857, 5882353]
我们看到相同的个数有3个,于是2430=3X10X3X3X3X3也可以得到正确的答案