相对于单音信号,正弦扫频信号即为在一定的频段范围内频率连续变化的信号。正弦扫频信号可作为系统激励和测取系统传递函数的较好方法。它主要实现对元器件、电路及整机的频率特性的测试,广泛应用在科研及生产等多个场合。同样地,在滤波器设计中,如果要知道滤波器的频率特性*。测量滤波器的脉冲响应,能够精确地获取频率特性。但是如果无法进行精确的数字的脉冲响应运算的话,那么用Sine Sweep波(频率逐渐变高的正弦波,也叫做频率扫描)来测量系统的频率特性是再适合不过的了。例如我们可以用Sine Sweep波来测量某个Mp3播放器的的频率特性,以及设置不同的EQ(均衡器)之后的频率特性。我们可以让播放器播放某个特定的Sine Sweep文件,用录音设备记录下它的输出声音,查看录下来的波形就能大概知道系统的频率特性了。 我们知道,频率的单位是赫兹(Hz),人耳能听到的频率范围是20-20000Hz,但人耳对Hz这种标度单位并不是线性感知关系。例如如果我们适应了1000Hz的音调,如果把音调频率提高到2000Hz,我们的耳朵只能觉察到频率提高了一点点,根本察觉不到频率提高了一倍。
*谐波输入下,输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性,相位之差φ(ω)为相频特性,并称其指数表达形式 为系统的频率特性。 稳定系统的频率特性等于输出和输入的傅氏变换之比,而这正是频率特性在自控原理中的物理意义。
1kHz以下,越低的频率要越大声才能听起来有同等响度。
2kHz~5kHz之间为人耳最敏感的区域,而且人耳在低音量时比起高音量时对此区域敏感。
1kHz~2 KHz间人耳对音量的敏感度会稍差些。
6kHz以上,人耳的敏感度会逐步下降,但比起低频率来说,音量大小对人耳低频的敏感度影响高于5kHz以上频率。
整体来说,人耳对于中频的敏感度较佳,高低频在音量小时,人耳较不灵敏,但随着音量变大,人耳对各频率的反应差异性就慢慢变小了。

图中显示了人耳对声音频率感知图,并不是线性感知关系,于是为了符合人类的听觉特性,通常频率响应图的频率轴都采用对数坐标。因此我们要产生的Sweep波的频率变化就需要成指数增长。
sine sweep正弦扫频信号推导如下:

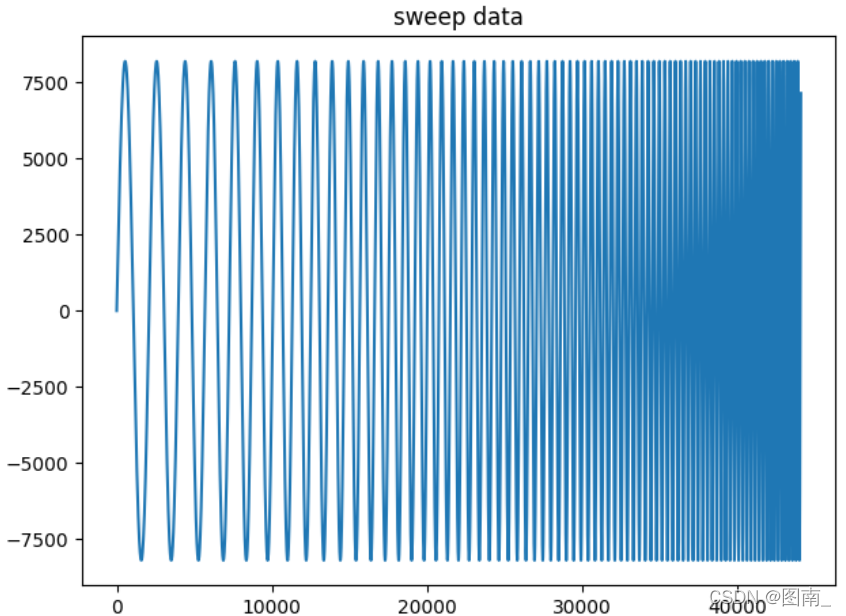
?用python画出正弦扫频信号如下:(频率从20Hz到200Hz,扫频时间为1秒):
SAMPLING_RATE = 44100
SWEEP_TIME = 1
F0 = 20
F1 = 200
PEAK = 0x2000
data = sinesweep(F0, F1, SWEEP_TIME, SAMPLING_RATE, PEAK)
plt.title("sweep data")
plt.plot(data)
plt.show()
def sinesweep(f0, f1, sweeptime, samplingrate, peak):#扫频信号:起始频率f0、截止频率f1、采样率和幅度
k = exp(log(float(f1) / f0) / sweeptime)#增长系数k的计算公式
data_len = sweeptime * samplingrate#数据长度
data = array.array('i', [0] * data_len)#创建一个长度为数据长度的全为0的int类型数组,用以存储每个采样点的幅度值
dt = 1.0 / samplingrate#两个采样点的相隔时间
t = 0.0#起始时间
p = 2 * pi * f0 / log(k)
for i in range(data_len):
data[i] = int(peak * sin(p * (pow(k, t) - 1)))#将每个采样点的幅度值存入数组
t += dt#每次加一个时间间隔
return data扫频信号如下图: