[Python知识库]用硬币抛掷模型进行置信度区间T-校验的EXCEL TINV和PYTHON的综合模拟

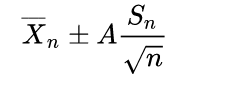
我了解了如上的置信度区间计算方法，其中Xn为样本采样数量的平均值（即mean），A为EXCEL TINV求出的偏离中心值，Sn为方差，n为采样样本总数。
我决定用硬币抛掷模型进行EXCEL TINV和PYTHON的综合模拟。首先我在EXCEL上对自由度为10和56765439的情况进行了计算

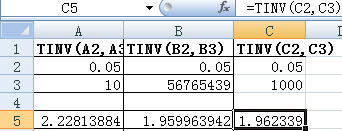
结果分别为：P1=2.22813884% P2=1.959963942% P3=1.962339%

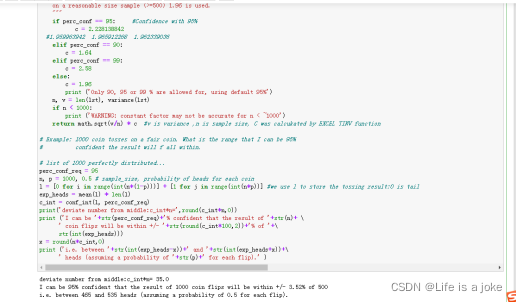
利用python进行分别用P1=2.22813884% P2=1.959963942% P3=1.962339%模拟后：投掷出head次数的区间分别为[465,535]和[469,531]和[469,531]。
因此可以发现：当我们采用自由度更大的值去估算置信区间参数的时候，获得的置信区间更小，对统计结果的精确性有很大的帮助。因此要尽量增加估计置信区间参数的自由度，使其进入变化小的稳定区间。

from __future__ import division
import math
  
def mean(lst):
    # μ = 1/N Σ(xi)
    return sum(lst) / float(len(lst))
 
def variance(lst):
    """
    Uses standard variance formula (sum of each (data point - mean) squared)
    all divided by number of data points
    """
    # σ2 = 1/N Σ((xi-μ)2)
    mu = mean(lst)
    return 1.0/len(lst) * sum([(i-mu)**2 for i in lst])
 
def conf_int(lst, perc_conf=95):
    """
    Confidence interval - given a list of values compute the square root of
    the variance of the list (v) divided by the number of entries (n)
    multiplied by a constant factor of (c). This means that I can
    be confident of a result +/- this amount from the mean.
    The constant factor can be looked up from a table, for 95% confidence
    on a reasonable size sample (>=500) 1.96 is used.
    """
    if perc_conf == 95:     #Confidence with 95%
           c = 1.962339
  #1.959963942  1.962339  2.228138842
    elif perc_conf == 90:
        c = 1.64
    elif perc_conf == 99:
        c = 2.58
    else:
        c = 1.96
        print ('Only 90, 95 or 99 % are allowed for, using default 95%')
    n, v = len(lst), variance(lst)
    if n < 1000:
        print ('WARNING: constant factor may not be accurate for n < ~1000')
    return math.sqrt(v/n) * c  #v is variance ,n is sample size, C was calcukated by EXCEL TINV function

# Example: 1000 coin tosses on a fair coin. What is the range that I can be 95%
#          confident the result will f all within.
 
# list of 1000 perfectly distributed...
perc_conf_req = 95
n, p = 1000, 0.5 # sample_size, probability of heads for each coin
l = [0 for i in range(int(n*(1-p)))] + [1 for j in range(int(n*p))] #we use l to store the tossing result:0 is tail 
exp_heads = mean(l) * len(l)
c_int = conf_int(l, perc_conf_req)
print('deviate number from middle:c_int*n=',round(c_int*n,0)) 
print ('I can be '+str(perc_conf_req)+'% confident that the result of '+str(n)+ \
      ' coin flips will be within +/- '+str(round(c_int*100,2))+'% of '+\
      str(int(exp_heads)))
x = round(n*c_int,0)
print ('i.e. between '+str(int(exp_heads-x))+' and '+str(int(exp_heads+x))+\
      ' heads (assuming a probability of '+str(p)+' for each flip).' )