1. 理论基础
logistic回归的因变量可以是二分类的,也可以是多分类的,一般情况下,我们比较常用的是二分类,也更容易理解,多分类问题可以使用softmax方法进行处理。
logistic回归是一种广义线性回归(generalized linear model),与多重线性回归分析有很多相同之处。
- 相同点
它们的模型形式基本上相同,都具有 w x + b wx + b wx+b,其中 w w w和 b b b是待求参数。
- 不同点
其区别在于他们的因变量不同。
- 多重线性回归直接将 w x + b wx+b wx+b作为因变量,即 y = w x + b y =wx+b y=wx+b。
- logistic回归则通过函数 L L L将 w x + b wx+b wx+b对应一个隐状态 p p p, p = L ( w x + b ) p =L(wx+b) p=L(wx+b),然后根据 p p p 与 1 ? p 1-p 1?p的大小决定因变量的值。
如果 L L L是logistic函数,就是logistic回归,如果 L L L是多项式函数就是多项式回归
。
简而言之,logistic回归会在线性回归后再加一层logistic函数的调用,如下所示:
p
(
Y
=
0
∣
x
)
=
1
1
+
e
w
x
+
b
p(Y=0|x)=\frac{1}{1+e^{wx+b}}
p(Y=0∣x)=1+ewx+b1?
p
(
Y
=
1
∣
x
)
=
1
?
p
(
Y
=
0
∣
x
)
=
e
w
x
+
b
1
+
e
w
x
+
b
p(Y=1|x)=1- p(Y=0|x)=\frac{e^{wx+b}}{1+e^{wx+b}}
p(Y=1∣x)=1?p(Y=0∣x)=1+ewx+bewx+b?
其中
w
w
w是权重,
b
b
b是偏置。
现在假设一个事件发生的几率是指该事件发生的概率与不发生的概率的比值,它的对数形式如下:
l
o
g
i
t
(
p
)
=
log
?
p
1
?
p
=
w
x
+
b
logit(p)=\log\frac{p}{1-p}=wx+b
logit(p)=log1?pp?=wx+b
所以在Logistic回归模型中,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数,这也就是Logisti回归名称的由来,即当 p > 1 ? p p > 1-p p>1?p时,上式会大于0,当 p < 1 ? p p < 1-p p<1?p时,上式会小于0,也就是说线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近负无穷,概率值就越接近0。
2. 代码示例
下列示例的步骤:
数据生成:由正态分布生成 ( x 1 , x 2 ) (x_1,x_2) (x1?,x2?)的数据对,并且以 x 1 x_1 x1?为例,将数据划分为pos和neg两部分,label为真值。数据显示:使用matplotlib画出pos和neg的数据分布图自定义模型:使用nn.Linear(2,1)指定输入输出的维度,输入是坐标值,所以是2维。使用nn.Sigmoid()指定使用逻辑回归损失函数和优化器的选择:BCE损失和SGD优化器。开始训练:迭代num_epochs,每10000次显示一次图。
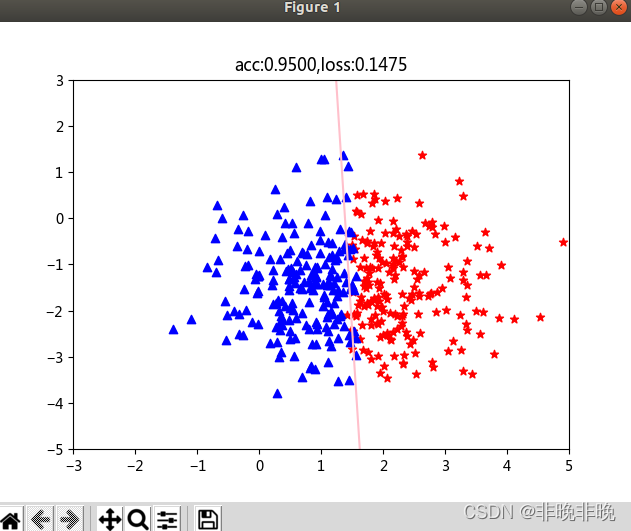
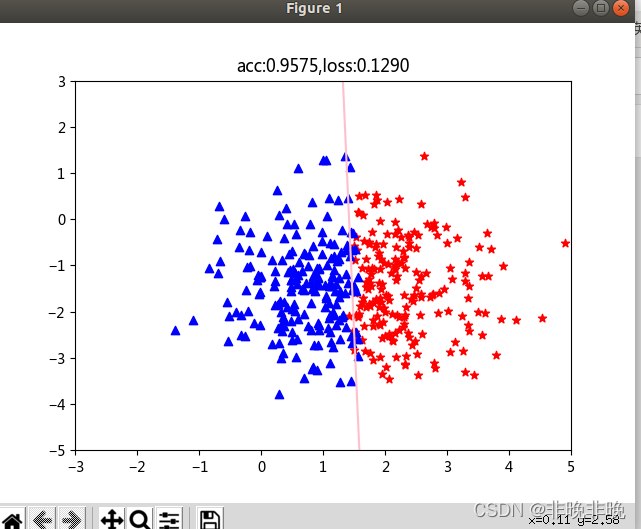
显示的直线为 x 1 ? w 0 + x 2 w 1 + b = 0 x_1*w_0 + x_2w_1 + b = 0 x1??w0?+x2?w1?+b=0,其实就是上面的 w x + b = 0 wx+b = 0 wx+b=0的分界线。
import torch
import matplotlib.pyplot as plt
import numpy as np
#-------------------------------------数据准备--------------------------------------
x1 = torch.randn(400)+1.5 # 生成400个满足标准正态分布的数字,均值为“0”,方差为“1”
x2 = torch.randn(400)-1.5
data = zip(x1.data.numpy(),x2.data.numpy()) #转numpy,组成元组
pos = []
neg = []
def classification(data):
for i in data:
if (i[0] > 1.5+0.1*torch.rand(1).item()*(-1)**torch.randint(1,10,(1,1)).item()): #item获取元素值,按照1.5分为左右两边
pos.append(i)
else:
neg.append(i)
classification(data)
#数据:pos and neg
inputs = [[i[0],i[1]] for i in pos] #数据维度2,由x1和x2组成
inputs.extend([[i[0],i[1]] for i in neg]) #extend 接受一个参数,这个参数总是一个 list,并且把这个 list 中的每个元素添加到原 list 中
inputs = torch.Tensor(inputs) # torch.Tensor 生成单精度浮点类型的张量
#标签,真值,1 and 0
label = [1 for i in range(len(pos))]
label.extend(0 for i in range(len(neg)))
label = torch.Tensor(label)
#-------------------------------------数据显示--------------------------------------
pos_x = [i[0] for i in pos]
pos_y = [i[1] for i in pos]
neg_x = [i[0] for i in neg]
neg_y = [i[1] for i in neg]
plt.scatter(pos_x,pos_y,c = 'r',marker = "*")
plt.scatter(neg_x,neg_y,c = 'b',marker = "^")
plt.show() #显示正反例
#-------------------------------------自定义模型--------------------------------------
import torch.nn as nn
class LogisticRegression(nn.Module):
def __init__(self):
super(LogisticRegression, self).__init__() #初始化父类
self.linear = nn.Linear(2,1) #输入2维,输出1维
self.sigmoid = nn.Sigmoid()
def forward(self,x):
return self.sigmoid(self.linear(x))
#------------------------损失函数、优化器的选择----------------------------
model = LogisticRegression() #使用cpu
criterion = nn.BCELoss() #Binary CrossEntropyLoss,用于二分类
optimizer = torch.optim.SGD(model.parameters(),0.01)
#------------------------开始训练----------------------------
num_epochs = 500000
for i in range(num_epochs):
out = model(inputs)
#print(out.shape)
loss = criterion(out.squeeze(1),label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
#-------------------------------------测试--------------------------------------
# 分类任务准确率,ge表示大于等于
acc = (out.ge(0.5).float().squeeze(1)==label).sum().float()/inputs.size()[0]
if (i % 10000 ==0):
plt.scatter(pos_x, pos_y, c='r', marker="*")
plt.scatter(neg_x, neg_y, c='b', marker="^")
weight = model.linear.weight[0]
#print(weight.shape)
wo = weight[0]
w1 = weight[1]
b = model.linear.bias.data[0]
# 绘制分界线
test_x = torch.linspace(-10,10,500) # 500个点
test_y = (-wo*test_x - b) / w1
plt.plot(test_x.data.numpy(),test_y.data.numpy(),c="pink")
plt.title("acc:{:.4f},loss:{:.4f}".format(acc,loss))
plt.ylim(-5,3) #刻度范围
plt.xlim(-3,5)
plt.show()
原始数据结果
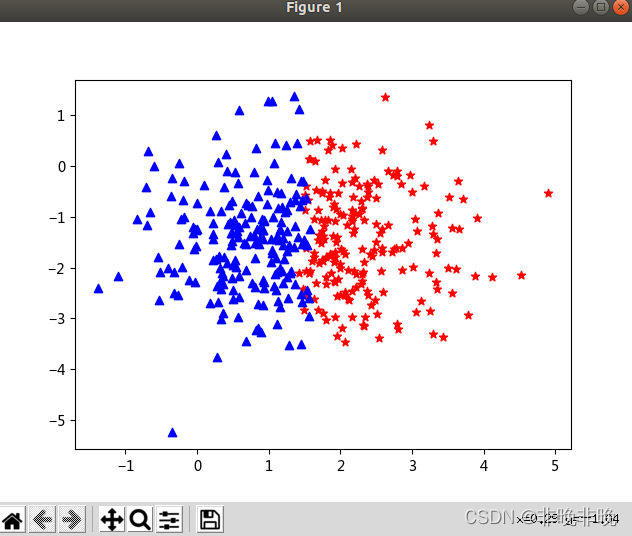
迭代结果: