
SciPy 是 Python 里处理科学计算 (scientific computing) 的包,使用它遇到问题可访问它的官网 (https://www.scipy.org/). 去找答案。 在使用 scipy 之前,需要引进它,语法如下:
import scipy
这样你就可以用 scipy 里面所有的内置方法 (build-in methods) 了,比如插值、积分和优化。
numpy.interpolatenumpy.integratenumpy.optimize
但是每次写 scipy 字数有点多,通常我们给 scipy 起个别名 sp,用以下语法,这样所有出现 scipy 的地方都可以用 sp 替代。
import scipy as sp
SciPy 是建立 NumPy 基础上的,很多关于线性代数的矩阵运算在 NumPy 都能做,因此就不重复在这里讲了
插值
给定一组 (xi, yi),其中 i = 1, 2, …, n,而且 xi 是有序的,称为「标准点」。插值就是对于任何新点 xnew,计算出对应的 ynew。换句话来说,插值就是在标准点之间建立分段函数 (piecewise function),把它们连起来。这样给定任意连续 x 值,带入函数就能计算出任意连续 y 值。
在 SciPy 中有个专门的函数 scipy.interpolate 是用来插值的,首先引进它并记为 spi。
import scipy.interpolate as spi
简单例子
用 scipy.interpolate 来插值函数 sin(x) + 0.5x。
基本概念
首先定义 x 和函数 f(x):
x = np.linspace(-2 * np.pi, 2 * np.pi, 11)
f = lambda x: np.sin(x) + 0.5 * x
f(x)
array([-3.14159265, -1.56221761, -1.29717034, -1.84442231,
-1.57937505, 0. , 1.57937505, 1.84442231,
1.29717034, 1.56221761, 3.14159265])
接下来介绍 scipy.interpolate 里面两大杀器:splrep 和 splev。两个函数名称都是以 spl 开头,全称 spline (样条),可以理解这两个函数都和样条有关。不同的是,两个函数名称以 rep 和 ev 结尾,它们的意思分别是:
- rep:representation 的缩写,那么 splrep 其实生成的是一个「表示样条的对象」
- ev:evaluation 的缩写,那么 splev 其实用于「在样条上估值」
splrep 和 splev 像是组合拳 (one two punch) - 前者将 x, y 和插值方式转换成「样条对象」tck
- 后者利用它在 xnew 上生成 ynew
一图胜千言:

接下来仔细分析一下 tck。
tck = spi.splrep( x, f(x), k=1 )
tck
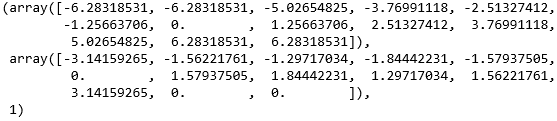
tck 就是样条对象,以元组形式返回,tck 这名字看起来很奇怪,实际指的是元组 (t, c, k) 里的三元素:
- t - vector of knots (节点)
- c - spline cofficients (系数)
- k - degree of spline (阶数)
对照上图,tck 确实一个元组,包含两个 array 和一个标量 1,其中
- 第一个 array 是节点,即标准点,注意到一开始 x 只有 11 个,但现在是 13 个,首尾都往外补了一个和首尾一样的 x
- 第二个 array 是系数,注意它就是 y 在尾部补了两个 0
- 标量 1 是阶数,因为在调用 splrep 时就把 k 设成 1
注:前两个 array 我只是发现这个规律,但解释不清楚为什么这样。它和 matlab 里面的 spline() 的产出不太一样,希望懂的读者可以留言区解释一下。
虽然解释不清楚前两个 array,那就把 tck 当成是个黑匣子 (black-box) 直接用了。比如可用 PPoly.from_spline 来查看每个分段函数的系数。
pp = spi.PPoly.from_spline(tck)
pp.c.T
array([[ 1.25682673, -3.14159265],
[ 1.25682673, -3.14159265],
[ 0.21091791, -1.56221761],
[-0.43548928, -1.29717034],
[ 0.21091791, -1.84442231],
[ 1.25682673, -1.57937505],
[ 1.25682673, 0. ],
[ 0.21091791, 1.57937505],
[-0.43548928, 1.84442231],
[ 0.21091791, 1.29717034],
[ 1.25682673, 1.56221761],
[ 1.25682673, 3.14159265]])
tck 的系数数组里有 13 个元素,而上面数组大小是 (12, 2),12 表示 12 段,2 表示每段线性函数由 2 个系数确定。
把 x 和 tck 丢进 splev 函数,我们可以插出在 x 点对应的值 iy。
iy = spi.splev( x, tck )
iy
用 Matplotlib 来可视化插值的 iy 和原函数 f(x) 发现 iy 都在 f(x) 上。Matplotlib 是之后的课题,现在读者可忽略其细节。

除了可视化,我们还可以用具体的数值结果来评估插值的效果:
np.allclose(f(x), iy)
np.sum((f(x) - iy) ** 2) / len(x)
True
0.0
第一行 allclose 的结果都是 True 证明插值和原函数值完全吻合,第二行就是均方误差 (mean square error, MSE),0.0 也说明同样结果。
上面其实做的是在「标准点 x」上插值,那得到的结果当然等于「标准点 y」了。这种插值确实意义不大,但举这个例子只想让大家
4. 明晰 splrep 和 splev 是怎么运作的
5. 如何可视化插出来的值和原函数的值
6. 如何用 allclose 来衡量插值和原函数值之间的差异
正规例子
上面在「标准点 x」上插值有点作弊,现在我们在 50 个「非标准点 xd」上线性插值得到 iyd。
xd = np.linspace( 1.0, 3.0, 50 )
iyd = spi.splev( xd, tck )
print( xd, '\n\n', iyd )

密密麻麻的数字啥都看不出来,可视化一下把。


这插得是个什么鬼?红色插值点在第二段和深青色原函数差别也太远了吧 (MSE 也显示有差异)。
np.sum((f(xd) - iyd) ** 2) / len(xd)
0.011206417290260647
问题出在哪儿呢?当「标准点 x」不密集时 (只有 11 个),分段线性函数来拟合 sin(x) + 0.5x 函数当然不会太好啦。那我们试试分段三次样条函数 (k = 3)。
tck = spi.splrep( x, f(x), k=3 )iyd = spi.splev( xd, tck )
可视化一下并计算 MSE 看看

np.sum((f(xd) - iyd) ** 2) / len(xd)
1.6073247177220542e-05
视觉效果好多了!误差小多了!
定义信号
import numpy as np
t = np.arange(0, 0.3, 1/20000.0)
x = np.cos(2*np.pi*1000*t) * (np.cos(2*np.pi*20*t) + np.cos(2*np.pi*8*t) + 3.0)
可视化

用极大值极小值方法计算信号的包络
import scipy as sp
import scipy.interpolate as spi
peak_id_up, peak_property_up = signal.find_peaks(x)
print(peak_id)
print(x[peak_id])
print(peak_property)
peak_id_down, peak_property_down = signal.find_peaks(-x)
tck_up = spi.splrep(n[peak_id_up], x[peak_id_up],k=3)
iy_up = spi.splev(n,tck_up)
tck_down = spi.splrep(n[peak_id_down],x[peak_id_down], k=3)
iy_down = spi.splev(n,tck_down)
plt.plot(x ,'k')
plt.plot(nt[peak_id_up], x[peak_id_up], 'ro')
plt.plot(nt[peak_id_down],x[peak_id_down],'go')
plt.plot(nt, iy_up,'r-',label = 'up')
plt.plot(nt,iy_down,'g-',label ='down')
plt.legend()
# plt.plot(y_new)
