概念
sympy是一个Python的科学计算库,用一套强大的符号计算体系完成诸如多项式求值、求极限、解方程、求积分、微分方程、级数展开、矩阵运算等等计算问题。
常用的sympy内置符号
虚数单位i
In [13]: import sympy
In [14]: sympy.I
Out[14]: I
In [15]: sympy.I ** 2
Out[15]: -1
#求-1的平方根
In [16]: sympy.sqrt(-1)
Out[16]: I
注;后面省略import sympy
自然对数的底e
In [18]: sympy.E
Out[18]: E
# 求对数
In [20]: sympy.log(sympy.E)
Out[20]: 1
无穷大00
In [26]: 1/sympy.oo
Out[26]: 0
In [27]: 1 + sympy.oo
Out[27]: oo
圆周率pi
In [60]: sympy.pi
Out[60]: pi
In [61]: sympy.sin(sympy.pi/2)
Out[61]: 1
用sympy进行初等运算
求对数
# 自然对数
In [10]: sympy.log(sympy.E)
Out[10]: 1
In [11]: sympy.log(sympy.E ** 3)
Out[11]: 3
# 以10为底1000的对数
In [12]: sympy.log(1000,10)
Out[12]: 3
求平方根
#求8的3次方根
In [15]: sympy.root(8,3)
Out[15]: 2
求j阶乘方
In [35]: sympy.factorial(4)
Out[35]: 24
求三角函数
n [86]: sympy.sin(sympy.pi)
Out[86]: 0
In [87]: sympy.sin(sympy.pi/2)
Out[87]: 1
表达式与表达式求值
sympy可以用一套符号系统来表示一个表达式,如函数、多项式等,并且可以进行求值,比如:
# 首先定义x为一个符号,表示一个变量
In [96]: x = sympy.Symbol('x')
In [97]: fx = 2*x + 1
# 可以看到fx是一个sympy.core.add.Add类型的对象,也就是一个表达式
In [98]: type(fx)
Out[98]: sympy.core.add.Add
# 用evalf函数,传入变量的值,对表达式进行求值
In [101]: fx.evalf(subs={x:2})
Out[101]: 5.00000000000000
还支持多元表达式:
In [102]: x,y = sympy.symbols('x y')
In [103]: f = 2 * x + y
# 以字典的形式传入多个变量的值
In [104]: f.evalf(subs = {x:1,y:2})
Out[104]: 4.00000000000000
# 如果只传入一个变量的值,则原本输出原来的表达式
In [105]: f.evalf(subs = {x:1})
Out[105]: 2.0*x + y
用sympy解方程(组)
使用sympy.solve函数解方程,该函数通常传入两个参数,第1个参数是方程的表达式(把方程所有的项移到等号的同一边形成的式子),第2个参数是方程中的未知数。函数的返回值是一个列表,代表方程的所有根(可能为复数根)。
解最简单的方程
比如下面求两个方程
# 首先定义 `x`为一个符号,代表一个未知数
In [24]: x = sympy.Symbol('x')
# 解方程:x - 1 = 0
In [25]: sympy.solve(x - 1,x)
Out[25]: [1]
# 解方程:x ^ 2 - 1 = 0
In [26]: sympy.solve(x ** 2 - 1,x)
Out[26]: [-1, 1]
# 解方程:x ^ 2 + 1 = 0
In [27]: sympy.solve(x ** 2 + 1,x)
Out[27]: [-I, I]
把函数式赋给一个变量
import sympy
x = sympy.Symbol('x')
fx = x + 1
a = sympy.solve(fx, x)
print(a)
print(type(fx))
j解方程组
比如要解这么一个一次方程组:

代码如下:
# 一次性定义多个符号
In [28]: x,y = sympy.symbols('x y')
In [29]: sympy.solve([x + y - 1,x - y -3],[x,y])
Out[29]: {x: 2, y: -1}
计算求和式
计算求和式可以使用sympy.summation函数,其函数原型为:sympy.summation(f, *symbols, **kwargs)。
举例:

In [37]: n = sympy.Symbol('n')
In [38]: sympy.summation(2 * n,(n,1,100))
Out[38]: 10100
如果sympy.summation函数无法计算出具体的结果,那么会返回求和表达式。
解带有求和公式的方程
例:

import sympy
x = sympy.Symbol('x')
i = sympy.Symbol('i',integer = True)
fx = sympy.summation(x, (i, 1, 5) )+10*x -15
a = sympy.solve(fx, x)
print(a)
注释:integer–整数,是numeric的一部分
求极限
求极限用sympy.limit函数。


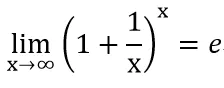
In [53]: x = sympy.Symbol('x')
In [54]: f1 = sympy.sin(x)/x
In [55]: sympy.limit(f1,x,0)
Out[55]: 1
In [56]: f2 = (1+x)**(1/x)
In [57]: sympy.limit(f2,x,0)
Out[57]: E
In [58]: f3 = (1+1/x)**x
In [59]: sympy.limit(f3,x,sympy.oo)
Out[59]: E
求导
求导使用sympy.diff函数,传入2个参数:函数表达式和变量名,举例如下:
In [63]: x = sympy.Symbol('x')
In [64]: f = x ** 2 + 2 * x + 1
In [65]: sympy.diff(f,x)
Out[65]: 2*x + 2
In [66]: f2 = sympy.sin(x)
In [67]: sympy.diff(f2,x)
Out[67]: cos(x)
# 多元函数求偏导
In [68]: y = sympy.Symbol('y')
In [70]: f3 = x**2 + 2*x + y**3
In [71]: sympy.diff(f3,x)
Out[71]: 2*x + 2
In [72]: sympy.diff(f3,y)
Out[72]: 3*y**2
求定积分
使用sympy.integrate函数求定积分,其功能比较复杂,非常强大,下面仅仅举几个比较简单的例子。
先来求一个最简单的积分:
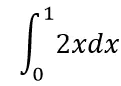
用牛顿-莱布尼兹公式可以立马口算出上面这个式子的结果是1,用代码计算如下:
n [74]: x = sympy.Symbol('x')
n [75]: f = 2 * x
# 传入函数表达式和积分变量、积分下限、上限
n [76]: sympy.integrate(f,(x,0,1))
ut[76]: 1
求不定积分
同样也是使用sympy.integrate函数求不定积分,下面仅仅举几个比较简单的例子。
比如求下面这个不定积分:

下面用代码来计算这个不定积分的结果:
In [79]: x = sympy.Symbol('x')
In [80]: f = sympy.E ** x + 2 * x
In [81]: sympy.integrate(f,x)
Out[81]: x**2 + exp(x)