文章目录
数据介绍
传送门
一段值是value,一段值是时间

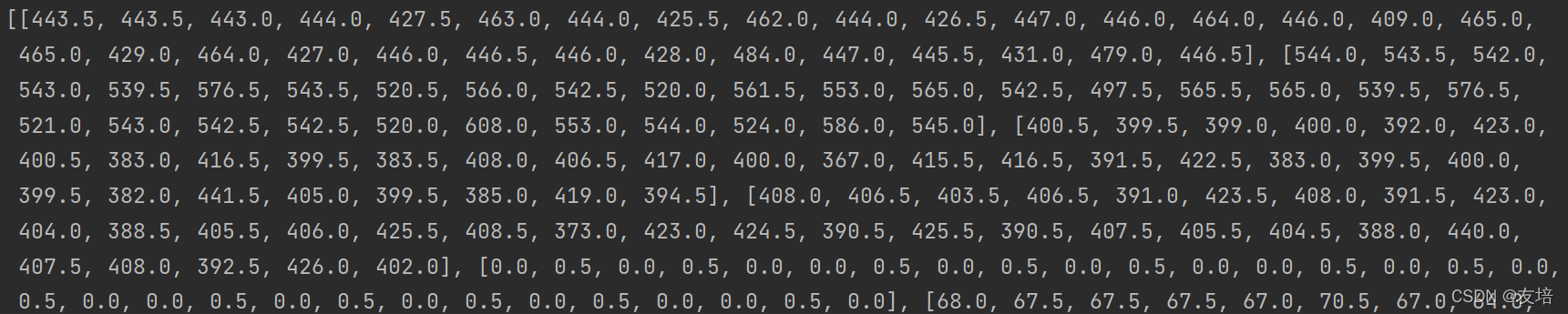
index_array处理后数据为下图,可以理解为联合index,具有唯一性

value_array处理后数据为下图,可以理解为,每一个小列表对应上图的一个index,31天数据,一共24个index
python一二次平滑指数法
误差采用的是均方误差
# -*- coding: utf-8 -*-
# @Time : 2022-04-07 15:44
# @Author : XiaoYouPei
# @File : exponential_smoothing.py
# @Software: PyCharm
# @desc: 一次、二次指数平滑预测法
import pandas as pd
import numpy as np
import copy
def data_access():
"""
数据接入
:return:
"""
source_data = pd.read_csv('./xxxxx机房耗电量.csv')
data_value = pd \
.DataFrame(source_data, columns=['device_id', 'mete_id', 'value'])
# 变更类型
data_value[['device_id', 'mete_id']] = data_value[['device_id', 'mete_id']].astype(object)
# 数据列表,每行表示一个测点历史数据
value_array = []
# id列表,每一个元素表示一个测点id,类型是tuple(device_id,mete_id)
index_array = []
# 按照设备id、监控量id分组遍历
for i in data_value.groupby(by=['device_id', 'mete_id']):
# 存储每次遍历的value值
temp_value = []
for j in i[1].values:
temp_value.append(j[2])
value_array.append(temp_value)
index_array.append(i[0])
return index_array, value_array
def single_exponential_smoothing(index_array, value_array):
"""
一次指数平滑处理
:param index_array:
:param value_array:
:return:
"""
s1_1 = [] # 记录si值
for m in range(0, len(index_array)):
s1_1_temp = []
x = 0
# 指数平滑初始值此处用的是三值均值
for n in range(0, 3):
x = x + float(value_array[m][n])
x = x / 3
s1_1_temp.append(x)
s1_1.append(s1_1_temp)
# 保存α值,0.05-1等差数组,差值为0.05
alpha = np.arange(0.05, 1, 0.05)
# 保存所有测点的均方误差值
mse_array = []
# 遍历每一个alpha值
for z in alpha:
mse_array_temp = []
s1 = copy.deepcopy(s1_1) # 深拷贝,不影响对象间的引用,独立判断
# 遍历每一个测点
for i in range(0, len(value_array)):
mse = 0
# 遍历每一个测点历史数据
for j in range(0, len(value_array[i])):
# 一次指数平滑
s1[i].append(
float(z) * float(value_array[i][j]) + (1 - float(z)) * float(s1[i][j])
)
# 误差平方求和
mse = (float(s1[i][j]) - float(value_array[i][j])) ** 2 + mse
# 每一个测点的均方误差
mse = mse / int(len(value_array[i]))
mse_array_temp.append(mse)
mse_array.append(mse_array_temp)
# 找出最合适的alpha
alpha_fit = 0
mse_min = float("inf")
for i, j in zip(alpha, mse_array):
mse_sum = 0
for z in j:
mse_sum = mse_sum + z
if mse_min > mse_sum:
mse_min = mse_sum
alpha_fit = i
return format(alpha_fit, '.3f')
def second_exponential_smoothing(index_array, value_array, day):
"""
二次指数平滑处理
:param index_array:
:param value_array:
:param day:
:return:
"""
s2_1 = []
s2_2 = []
for m in range(0, len(index_array)):
s2_1_temp = []
x = 0
# 指数平滑初始值此处用的是三值均值
for n in range(0, 3):
x = x + float(value_array[m][n])
x = x / 3
s2_1_temp.append(x)
s2_1.append(s2_1_temp)
s2_2.append(s2_1_temp)
# 保存α值,0.05-1等差数组,差值为0.05
alpha = np.arange(0.05, 1, 0.05)
# 保存所有测点的均方误差值
mse_array = {}
s2_1_alpha_predicted = {}
s2_2_alpha_predicted = {}
# 遍历每一个alpha值
for z in alpha:
mse_array_temp = []
# 一次指数平滑
s2_1_predicted = []
for i in range(0, len(value_array)):
# 先固定shape
s2_1_temp = [[]] * len(index_array)
for j in range(0, len(value_array[i])):
# 第一次计算获取初始值
if j == 0:
s2_1_temp[i].append(
float(z) * float(value_array[i][j]) + (1 - float(z)) * float(s2_1[i][j])
)
else:
s2_1_temp[i].append(
float(z) * float(value_array[i][j]) + (1 - float(z)) * float(s2_1_temp[i][j - 1])
)
s2_1_predicted.append(s2_1_temp[i])
# 二次指数平滑
s2_2_predicted = []
for i in range(0, len(value_array)):
s2_2_temp = [[]] * len(index_array)
mse = 0
for j in range(0, len(value_array[i])):
if j == 0:
s2_2_temp[i].append(
float(z) * float(s2_1_predicted[i][j]) + (1 - float(z)) * float(s2_2[i][j])
)
else:
s2_2_temp[i].append(
float(z) * float(s2_1_predicted[i][j]) + (1 - float(z)) * float(s2_2_temp[i][j - 1])
)
# 误差平方求和
mse = (float(s2_2_temp[i][j]) - float(value_array[i][j])) ** 2 + mse
mse = mse / int(len(value_array[i]))
mse_array_temp.append(mse)
s2_2_predicted.append(s2_2_temp[i])
mse_array[z] = mse_array_temp
s2_1_alpha_predicted[z] = s2_1_predicted
s2_2_alpha_predicted[z] = s2_2_predicted
break
# 找出最合适的alpha
alpha_fit = 0
mse_min = float("inf")
for k, v in mse_array.items():
mse_sum = 0
for z in v:
mse_sum = mse_sum + z
if mse_min > mse_sum:
mse_min = mse_sum
alpha_fit = k
s2_1_predicted = s2_1_alpha_predicted[alpha_fit]
s2_2_predicted = s2_2_alpha_predicted[alpha_fit]
Xt = []
for i in range(0, len(value_array)):
At = (
float(s2_1_predicted[i][len(s2_1_predicted[i]) - 1]) * 2 -
float(s2_2_predicted[i][len(s2_2_predicted[i]) - 1])
)
Bt = (
float(alpha_fit) / (1 - float(alpha_fit)) * (
float(s2_1_predicted[i][len(s2_1_predicted[i]) - 1]) - float(
s2_2_predicted[i][len(s2_2_predicted[i]) - 1]))
)
Xt.append(At + Bt * int(day))
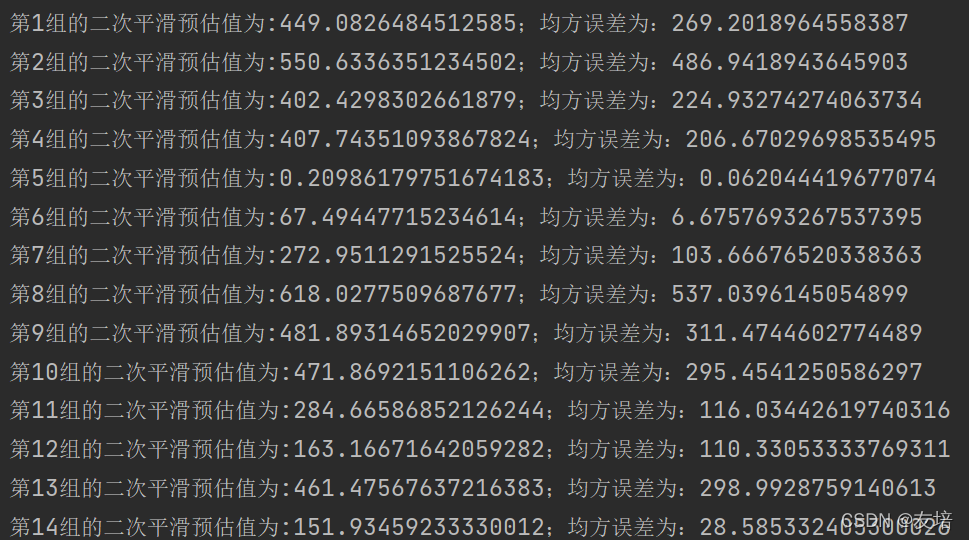
print('第' + str(i + 1) + '组的二次平滑预估值为:' + str(Xt[i]) + ';均方误差为:' + str(mse_array[alpha_fit][i]))
if __name__ == '__main__':
index_array, value_array = data_access()
print(index_array)
print(value_array)
# alpha_fit = single_exponential_smoothing(index_array, value_array)
# second_exponential_smoothing(index_array, value_array, 1)
二次指数平滑最终结果输出图
三次带更新,二次比较一次带了趋势概念,三次则具有季节性特征
