[Python知识库]数学：小明要如何在网球比赛中赢到一辆车？

有一道题：小明喜欢打网球，有一天他爹对他说：如果你在三盘中连赢 2 盘，就奖励你一辆车。

具体的规则是，小明以他爹和俱乐部冠军为对手，但不能连续选择一个人 2 次，所以只有以下两种比赛顺序：

A、爹 => 冠军 => 爹；

B、冠军 => 爹 => 冠军。

冠军的水平当然比他爹高。小明应该选择哪种顺序？按照直觉，似乎是选择 A 选项连赢两场的概率最大，但是事实如此吗？来看看。

首先先把不同的选择最后连赢两场的概率都画出来：

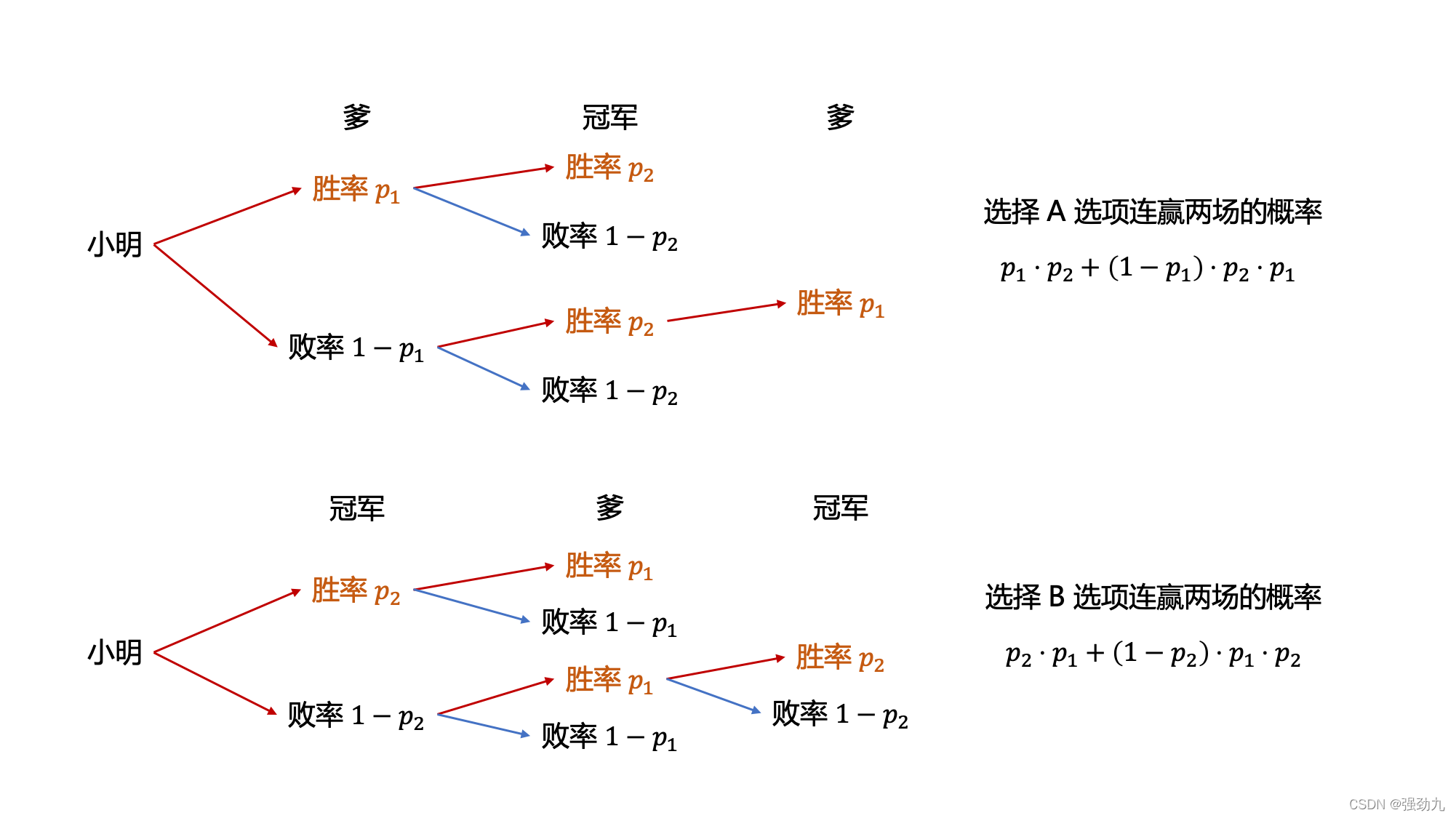
因为冠军的水平一定比他爹高，所以小明和赢冠军的概率 $p_1$ 大于赢他爹的概率 $p_2$.

我们用 Python 简单地编个程，算出 $p_1$ 与 $p_2$ 取不同值时候，选择 A 和 B 连赢两场的概率哪个更高。我们分别算出选项 A 和 B 连赢两场的概率，然后求出他们的比值，如果大于 1 则选择 A 选项概率更高，否则选择 B 概率更高。代码如下：

import numpy as np
import matplotlib.pyplot as plt

p1, p2 = np.linspace(0.0, 1), np.linspace(0.0, 1)  # 概率取 0. 会导致 NaN 出现
xs, ys = np.meshgrid(p1, p2)
zA = xs*ys + (1-xs)*ys*xs  # 选项 A、爹 => 冠军 => 爹 连赢两场的概率
zB = ys*xs + (1-ys)*xs*ys  # 选择 B、冠军 => 爹 => 冠军 连赢两场的概率
z = zA / zB  # 如果大于 1. 则选择 A 选项概率更高，否则选择 B 概率更高

# 将整个区域用等高线画图
plt.contourf(xs, ys, z)
plt.colorbar()  # 显示 color bar
plt.plot([0.0, 1.0], [0.0, 1.0], 'r--')  # 画一条 p1 = p2 的线

画出的图如下：

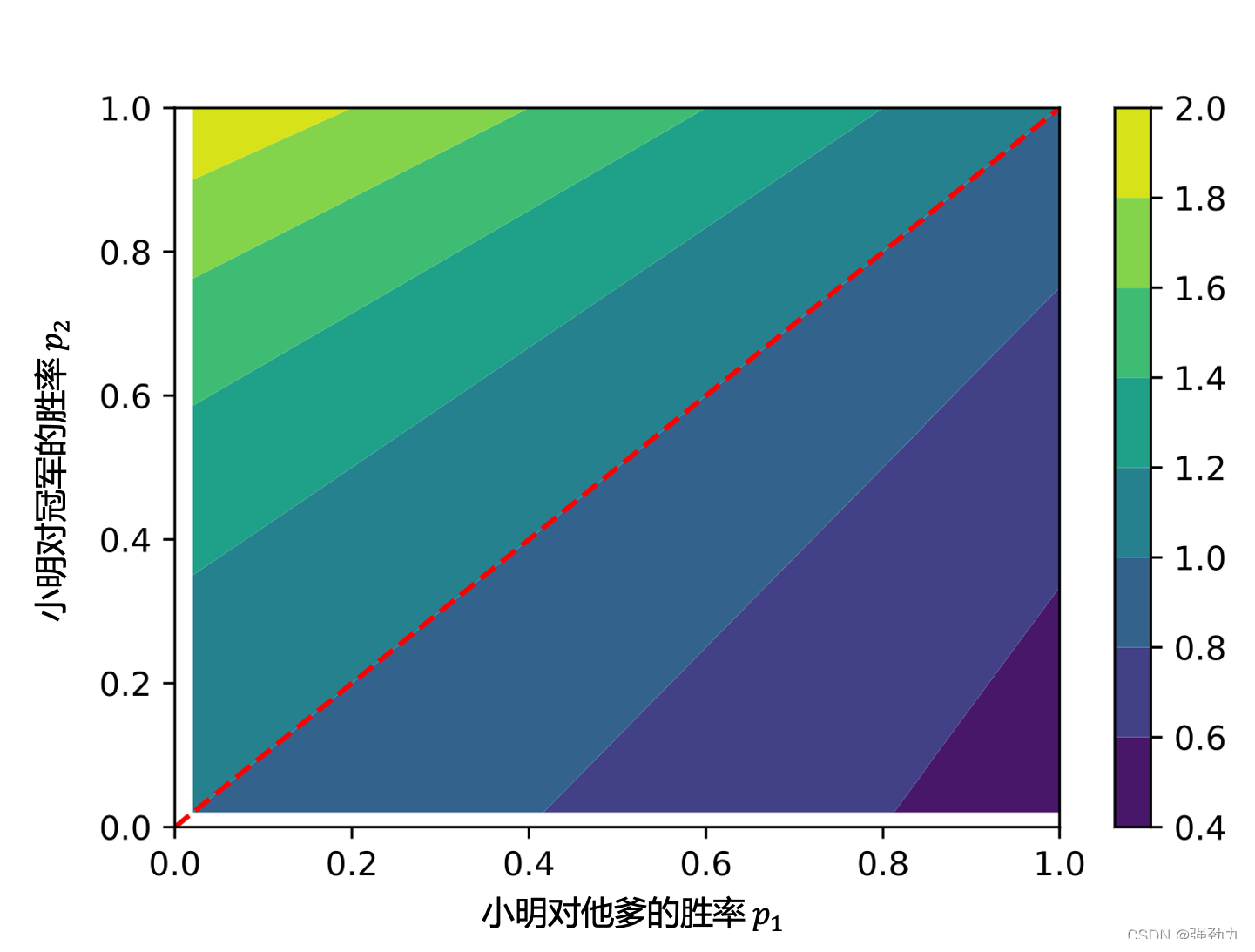
红色虚线右下方的区域，是 $p_1>p_2$ 也就是赢他爹的概率比赢冠军的概率更大（这也是符合常理的），从图中可以看到，只要小明赢他爹的胜率比赢冠军的胜率还大，那么最终求得选项 A 比选项 B 的值就小于零，换句话说，小明应该要选择 B 策略，才更加有可能连赢两场，获得他爹奖励的一辆车。

阅读世界，共赴山海

423全民读书节，邀你共读