网络放大器
问题描述
对于一个石油传送网络可由一个加权有向无环图G表示。该图中有一个称为源点的顶点S ( 保证S的入度为0 ) , 从S出发 , 石油流向图中的其他顶点 . G中每条边上的权重为它所连接的两点间的距离。
在输送石油的过程中 , 需要有一定的压力才能使石油从一个点到达另一个点,但压力会随着路程的增加而降低 ( 即压力的损失量是路程的函数 ) .
因此为了保证石油在网络的正常运输,在网络传输中必须保证在任何位置的压力都要不小于最小压力Pmin。为了维持这个最小压力,可在G中的一些或全部顶点放置压力放大器 , 压力放大器可以将压力恢复至该网络允许的最大压力Pmax。
可以设d为石油从压力Pmax降为压力Pmin所走的距离 , 在无压力放大器的情况下石油可运输的距离不超过d .
在该问题中 , 需要在G中放置最少的压力放大器 , 使得该传输网络从S出发,能够将汽油输送到图中的所有位置。
基本要求
1.针对该问题做出一定的合理分析和假设
2.确定输入的数据格式并给出数据生成器.
3.给出两种方法以解决上述问题,思考如何验证两种方法的正确性.
4.比较两种方法的时间和空间性能,用图表显示比较结果。
已经实现
- 使用分支定界和回溯解决了问题。
- 对程序的正确性有推导或对比: 将对拍程序封装成函数,并且验证了两个方法的正确性.
- 合理且完善的性能分析与图表展示: 使用python的matplotlib 实现了时间和空间性能用图表显示比较结果,进行了分析。
- 用库cyaron的数据生成器make.py 生成了部分数据进行了测试
- 使用dot作图的方法,实现了图的可视化方便验证正确性,可以直观的展示程序的结果 , 包括放大器的位置 , 每个位置的压力 , 边权等.
- 程序设计规范,封装良好,拥有详细的注释。
- 压缩包包括solution1.h solution2.h graph.h main.cpp 以及生成图表的testRoom.py testtime.py make.py
- GitHub实验代码
部分展示
一次跑完100个样例并且输出到文件,包括性能分析图表、每个样例的图片!


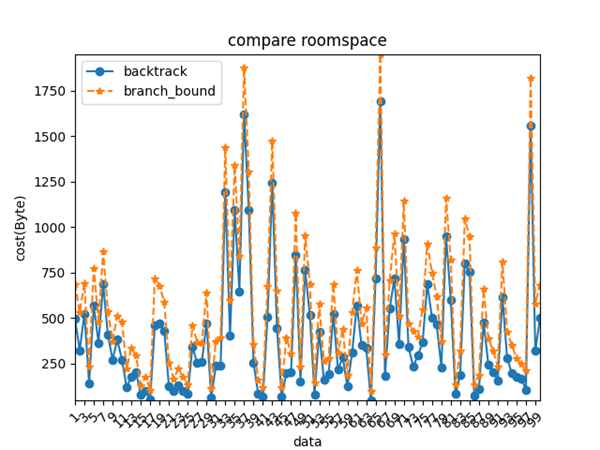
性能分析图表,时间和空间

结构
- graph.h 定义图结构DAG以及用于分支定界的子集树
- solution1.h 回溯算法实现
- sooluton2.h 分支定界算法实现
- main.cpp Drive Program
可视化
void visualize(int i)
使用dot作图 的方式进行画图验证正确性,只需要输入描述性语言,例如图的节点以及信息,边的信息,执行dot命令 就可以画出每个样例的图的信息的图片。
最后进行系统调用,把dot 作图成为jpg
void DAG::visualize(int i)
{//可视化
recountpre();
//system("cd C:\\Users\\12042\\Desktop\\dagData\\outputimage");
string name = to_string(i) + ".dot";
std::ofstream out(name);
out << "digraph g {\n";
for (int i = 1; i < nodes.size(); i++) {
out << i;
if (place_bst[i])
out << "[label=\"node" << i << ";pre = " << nodes[i].press << "\",style=filled, fillcolor=red];\n";
else
out << "[label=\"node" << i << ";pre = " << nodes[i].press << "\",style=filled, fillcolor=white];\n";
}
for (auto i = 1; i <= n; ++i) {
for (auto& edge : nodes[i].edges) {
out << i << "->" << edge.to << "[label=\"cost=" << edge.cost << "\"];\n";
}
}
out << "}\n";
out.close();
string order = "dot -Tjpg " + to_string(i) + ".dot -o solve" + to_string(i) + ".jpg";
system(order.c_str());
}
对拍
void check()
对拍程序即对自己程序的输出文件与标准(正确)答案的输出文件进行答案比对,如果完全相同,则证明正确性上没有问题,如果有不同,则证明正确性无法保证。 通常是单独写一个cpp文件,然后执行exe,鉴于本实验输出结果每个样例有且只有一个数字,所以把他封装成函数,每次输入STDOUTPUT的结果和自己的结果进行挨个比对,进行对拍即可!
void check() {
int flag = 0;
stringstream ss;
for (int i = 1; i <= 100; i++) {
cout << "正在测试数据集: " << i << "\n";
string opstd = "C:\\Users\\12042\\Desktop\\dagData\\outputSTD\\";
string myin = "C:\\Users\\12042\\Desktop\\dagData\\output\\";
opstd += to_string(i) + ".out";
myin += to_string(i) + ".out";
ifstream finstd(opstd);
if (!finstd.is_open()) {
cout << "文件打开失败\n";
}
int ans; finstd >> ans;
finstd.close();
ifstream finmy(myin);
if (!finmy.is_open()) {
cout << "文件打开失败\n";
}
int me; finmy >> me;
finmy.close();
if (me != ans) {
cout << "Wrong Answer\n";
ss << i << "WA!\n";
flag = 1;
}
else {
cout << "Accept\n";
}
}
if (!flag) {
cout << "All Accept!\n";
}
else cout << "Wrong Answer\n";
cout << ss.str();
}
基本算法
void topsort() 拓扑排序
因为各个顶点之间存在着前后关系,并且有源点,所以为了布置好放大器,必须要建立一个拓扑序列,根据拓扑序列进行油压的检测以及放大器的放置的判断。
具体思路:
①每次找出入度为0的点
②将这些顶点以及他们的出边删除
③记录删除的顺序作为拓扑序列。
④更新受影响的点的入度。
⑤重复1-4直到每个点都确定了一个拓扑次序。
void DAG::topsort()
{//确定一个拓扑序列 以便后续
int cnt = 1;
queue<int> q;
for (int i = 1; i <= n; i++) {
if (in_deg[i] == 0) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop();
nodes[u].toponum = cnt;
dig[cnt++] = u;//排序
for (auto e : nodes[u].edges) {
if (--in_deg[e.to] == 0)
q.push(e.to);
}
}
if (cnt < n) {
cout << "图中有环路!不符合要求!\n";
return;
}
//for (int i = 1; i <= n; i++)
//cout << "top " << i << " " << dig[i] << "\n";
}
回溯算法
第一种解决算法是使用回溯+剪枝的方式解决放大器放置的问题
回溯是按照DFS的策略从根节点开始出发,搜索解空间树(决策树),每个点都有可能放置或者不放置放大器,而这样的复杂度是 O ( 2 n ) O(2^n) O(2n) 为了降低复杂度,就必须使用剪枝函数,在搜索最优解的过程中对解空间进行剪枝,例如确定某点必须放置,或者确定某解空间必定不为最优解等等,来减少解空间的搜索次数。
具体思路
void DAG::backtracking(int level, int cnt)
level 是 搜索层数,n是节点个数,cnt是放置的放大器个数,best是指迄今为止记录的最优解
①level >= n时便求得了一个解,如果此时的cnt 更小,则是一个更优解,进行更新最优解的操作。
②如果level < n-1, 当前扩展的节点有两种可能,放置或者不放置,如果该点向其他点输送时,有的点油压<PMIN,则该点必须放置,剪掉不放置的情况,进行递归和回溯。其次,如果该点的油压<Pmin 则该点必须放置,剪掉不放置的情况,进行递归和回溯。否则,需要进行放置和不放置的两个决策的递归。
剪枝:
①如果在某层决策的时候,cnt以及大于best了,则不需要进行决策了,因为必然不是最优解。
②如果某点PRESS < PMIN 则必须放。 但是,事实上,从前向后按拓扑序决策,前面的决策已经保证了该点的油压>Pmin了,所以此种情况不会遇到!
③如果送去相邻节点PRESS < PMIN,必须放增压器,不需要考虑不放!
注意 :如果某点油压>=PMAX 或者说到其他节点都符合要求,也要考虑放置放大器,因为求最优解,此处不放置可能导致后面多个子节点放置,导致求出不为最优解的情况,所以两个决策都要考虑!
数据结构
回溯方法,需要考虑解空间树(决策树) 但是不需要实际建立,需要在每次决策中体现出来即可。之后维护level cnt分别作为决策的深度,以及放置的个数,用来剪枝和确定最优解。邻接表的表头node 存储每个点的信息,例如press 以及 booster,最后需要把信息输入到place_booster 数组,确定哪些点放了放大器。
// 回溯需要按照拓扑序跑! dfs
void DAG::backtracking(int level, int cnt)
{//进行回溯决策树里面 左是该节点不放 右子树是放
//搜索第level层
int u = dig[level];//当前点 level也代表了拓扑序
if (level >= n) {//最底层了
best_ans = min(cnt, best_ans);
//记录下最好的情况 不然会被冲了
//更新放置情况
for (int i = 1; i <= n; i++) {
place_bst[i] = false;
place_bst[i] = nodes[i].booster;
}
return;
}
if (level == 1) {//第一层 源点肯定放了(不算)只需要判断其他边 如果低了 就在v放
backtracking(2, 0);
}
else {//其他层 如果到v 不行 则在 u放
int j;
int flag = 0;
int temp_pre = -1;//临时变量pre 用来回溯!
//求press[u] 优化 用入边
//for (auto& c : nodes[u].inedges) {
// int f = c.from;
// if (nodes[f].toponum < nodes[u].toponum)
// {//必须是拓扑序前面的
// temp_pre = max(temp_pre, nodes[u].press - c.cost);
// }
//}
for (int k = 1; k < level; k++) {//求 前面到
for (auto& x : nodes[dig[k]].edges) {
if (x.to == u)
//nodes[u].press = max(nodes[u].press, nodes[dig[k]].press - x.cost);
temp_pre = max(temp_pre, nodes[dig[k]].press - x.cost);
}
}
for (j = 0; j < 2; j++)
{//进行两种决策
//剪枝1
if (temp_pre >= Pmax) {
backtracking(level + 1, cnt);
break;
}
//剪枝2
if (temp_pre < Pmin)
{
cnt++;
nodes[u].booster = true;
//剪枝3
if (cnt >= best_ans) {
return;
}
backtracking(level + 1, cnt);
}
if (j == 0) {//不放 但是需要
for (auto& v : nodes[u].edges) {//对于所有出边进行判断
int next_pr = temp_pre - v.cost;
if (next_pr < Pmin) {
flag = 1;
break;
}
}
}
//决策 put
if (j == 1 || flag == 1) {//放
cnt++;
nodes[u].press = Pmax;
nodes[u].booster = true;
//剪枝
if (cnt >= best_ans)
return;
else {
backtracking(level + 1, cnt);
}
}
//not put
else if (j == 0) {//对应的 j==0 && flag!=1
nodes[u].press = temp_pre;
nodes[u].booster = false;
backtracking(level + 1, cnt);
}
}
}
}
分支定界
最小耗费的优先队列 分支定界求解
分支定界采用子集树来表示解空间,但是每个活结点只有一次机会成为扩展结点,活结点一旦成为扩展节点,就会产生所有的儿子节点,不可能行的都丢弃。使用最小耗费分支定界的限界函数来进行生成和展开活结点数量。每次确定最小耗费的下限,即最少的cnt数。
具体思路
①最开始的活结点是根节点,之后求活结点的子节点进行判断其能否作为扩展结点。
②求出子节点压力,如果子节点有不符合要求的,则必须把该节点作为扩展结点,如果他符合不油压要求,则cnt++,作为活结点,否则两种情况作为活结点,直到level == n-1结束(最后一个一定不put)
数据结构
使用一个子集树节点 subsetnode (btnode) 里面存储每个扩展结点的父节点,即从哪来的,press,level,是否放放大器,以及bstnum,该路上已经放了多少个booster,以此max_to_cost,用来减少复杂度限界使用!之后进行求解,使用优先队列存储子集树节点,按照bstnum排序,最后求出的第一个level = n-1的解,即最优解!
//最小耗费 分支定界
void DAG::branch_bound()
{//分支定界 活结点--扩展结点-- 子集空间树
btnode* enode = new btnode(Pmax, 2);//活结点
int level = 2;
while (level <= n - 1)
{//进行活结点的拓展
int vert = dig[level];//该层扩展的节点
int temp_press = -1;
int flag = 0;
//求扩展结点的压力
for (int k = 1; k <= level - 1; k++) {
for (auto& e : nodes[dig[k]].edges) {
if (e.to == vert) {
btnode* p = enode;
//????
for (int j = level - 1; j > k; j--)
p = p->parent;
temp_press = max(temp_press, p->press - e.cost);
}
}
}
//限界函数 -最大花费 小必须放
if (temp_press - nodes[vert].max_to_cost < Pmin) {
flag = 1;
}
//check 到 邻接点是否符合要求
/*for (auto& e : nodes[vert].edges) {
if (temp_press < Pmin + e.cost) {
flag = 1; break;
}
}*/
if (flag == 0) {//两种 放或者放
btnode* t = new btnode(temp_press, level + 1, enode, enode->bstnum);
pq.push(t);
btnode* tt = new btnode(Pmax, level + 1, enode, enode->bstnum + 1);
tt->bst_here = true;
pq.push(tt);
}
else {//必须放
btnode* tt = new btnode(Pmax, level + 1, enode, enode->bstnum + 1);
tt->bst_here = true;
pq.push(tt);
}
enode = pq.top(); pq.pop();
level = enode->level;
}
best_ans = enode->bstnum;
btnode* p = enode;
while (p) {
place_bst[dig[p->level - 1]] = p->bst_here;
p = p->parent;
}
}
性能分析
进行性能对比,在跑每个样例的过程中记录一下时间,输出到文件中,并且计算每个样例所用的空间大小,输出到文件。
使用Python matplotlib作图,做出折线图对比性能。 使用LARGE_INTEGER + QueryPerformanceCounter() 统计时间
统计时间
LARGE_INTEGER start_time; //开始时间
LARGE_INTEGER end_time; //结束时间
double dqFreq; //计时器频率
LARGE_INTEGER freq; //计时器频率
QueryPerformanceFrequency(&freq);
dqFreq = (double)freq.QuadPart;
QueryPerformanceCounter(&start_time); //计时开始
DAG g;
g.topsort();
g.backtracking(1, 0);
fout << g.best_ans << "\n";
QueryPerformanceCounter(&end_time); //计时end
// write out!
ofstream fo("cost1.txt", ios::app);
double run_time = (end_time.QuadPart - start_time.QuadPart) / dqFreq * 1000;
fo << i << " " << run_time << "\n";
fo.close();
//空间 第一种 回溯
ofstream foo("room1.txt", ios::app);
//int 4 bool 1
ll romcost = 5 * g.n + 4 * g.m + 4 * g.n;
foo << i << " " << romcost << "\n";
foo.close();
测试time并画图的Python代码
import matplotlib.pyplot as plt
input_txt = 'cost1.txt'
x = []
y = []
z = []
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
x.append(int(line[0]))
y.append(float(line[1]))
f.close
input_txt = 'cost2.txt'
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
z.append(float(line[1]))
f.close
plt.plot(x, y, marker='o', label='backtrack')
plt.plot(x, z, marker='*', label='branch_bound',linestyle="--")
plt.xticks(x[0:len(x):2], x[0:len(x):2], rotation=45)
plt.margins(0)
plt.xlabel("data")
plt.ylabel("cost(ms)")
plt.title("compare time")
plt.tick_params(axis="both")
plt.legend()
plt.show()
测试空间性能并画图的Python代码,空间性能是我大致根据字节数计算的,没找到如何测量
import matplotlib.pyplot as plt
input_txt = 'room1.txt'
x = []
y = []
z = []
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
x.append(int(line[0]))
y.append(int(line[1]))
f.close
input_txt = 'room2.txt'
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
z.append(int(line[1]))
f.close
plt.plot(x, y, marker='o', label='backtrack')
plt.plot(x, z, marker='*', label='branch_bound',linestyle="--")
plt.xticks(x[0:len(x):2], x[0:len(x):2], rotation=45)
plt.margins(0)
plt.xlabel("data")
plt.ylabel("cost(Byte)")
plt.title("compare roomspace")
plt.tick_params(axis="both")
plt.legend()
plt.show()
结果展示
生成DAG的图片

具体DAG图片,红色mark 放大器的位置
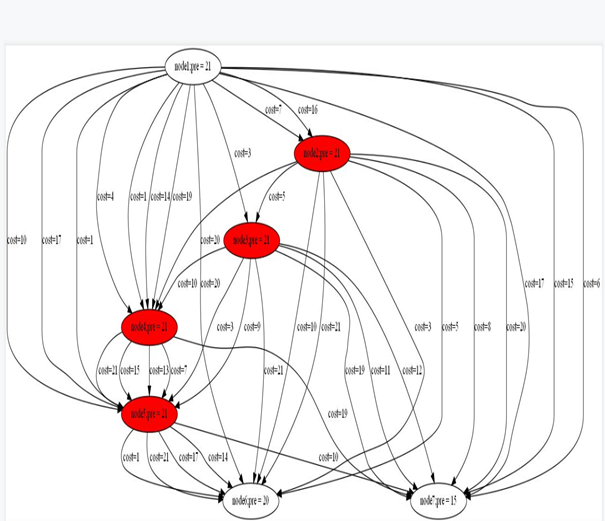
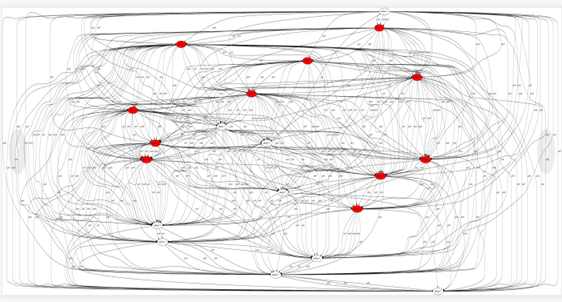
结果分析
复杂度
回溯和分支定界:时间复杂度都为O(2^n),但是经过剪枝和限界之后会远小于这个复杂度。
性能表现
回溯法和分支定界法,这两个算法都需要有一个限界函数,并且设计思想类似。对于这两个算法,时间复杂度都是O(2^n),虽然复杂度一样,但是在具体问题特别是数据较多的时候,由于回溯法即使找到了最优解也不能马上就肯定他是最优的,必须把所有可行解都求出来才能确定。而分支定界,只需要找到一个解,这个解必为最优的。分支定界比回溯法检查更少的情况和节点,时间性能更好。
但是在空间性能上:回溯法如果建立解空间的话,使用的内存是O(n)即最长路径的空间大小,而分支定界占用的内存为O(2^n)加之回溯法不需要真的建立节点,而分支定界需要建立节点,又多了一层空间代价。
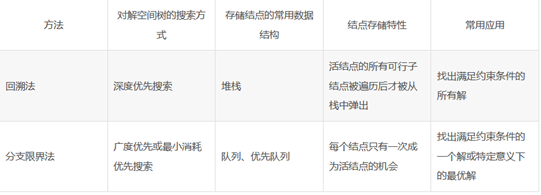
在回溯时,如果一个节点>Pmax并且临界点都>Pmin 不能直接剪去放置的情况,经过实验发现,Vi没放置,但是他的下一个临界点Vi+1 Vi+2… 可能会因为他们的下一个节点而放置,也就是放置了>1个。此时如果Vi 放置了,会提升他们的Press,可能他不需要额外放置,所以总共放置了1个,所以需要对两种决策都进行递归回溯。为此,我也删除了我的一个剪枝函数,才得到了最优解。
改进
- 可以尝试暴力算法求解
- 剪枝算法可以进一步优化剪枝,提高效率
- 在数据结构方面,或许可以考虑图结构的反转 ,根据使用频率来优化数据结构
- 计算所需空间性能,可以思考如何度量
- 优化整体项目结构,(现在回看写的太chou了~)
定他是最优的,必须把所有可行解都求出来才能确定。而分支定界,只需要找到一个解,这个解必为最优的。分支定界比回溯法检查更少的情况和节点,时间性能更好。
但是在空间性能上:回溯法如果建立解空间的话,使用的内存是O(n)即最长路径的空间大小,而分支定界占用的内存为O(2^n)加之回溯法不需要真的建立节点,而分支定界需要建立节点,又多了一层空间代价。
[外链图片转存中…(img-Zi8B3xRG-1651889072411)]
在回溯时,如果一个节点>Pmax并且临界点都>Pmin 不能直接剪去放置的情况,经过实验发现,Vi没放置,但是他的下一个临界点Vi+1 Vi+2… 可能会因为他们的下一个节点而放置,也就是放置了>1个。此时如果Vi 放置了,会提升他们的Press,可能他不需要额外放置,所以总共放置了1个,所以需要对两种决策都进行递归回溯。为此,我也删除了我的一个剪枝函数,才得到了最优解。
改进
- 可以尝试暴力算法求解
- 剪枝算法可以进一步优化剪枝,提高效率
- 在数据结构方面,或许可以考虑图结构的反转 ,根据使用频率来优化数据结构
- 计算所需空间性能,可以思考如何度量
- 优化整体项目结构,(现在回看写的太chou了~)
