🤡 前言🤡

问题产生背景：某天我们正在上着人工智能导论这门专业课，由于他与数学关联性灰常的大，所以听得我们是云里雾里，不知其然，不知其所以然。但是这天老师突然提起了大家一块玩拼图游戏。（八数码问题）这下提起了同学们的兴致，从老师那里得知八数码问题是一道典型的启发式搜索问题、还与广度优先遍历有关。这可极大地激发了我的兴趣。但是课堂上的我们却久久没能拿下以至于老师将其作为课后作业留给了我们。戏剧性的是某天我在备战蓝桥杯的时候，写到了一个九宫格问题,并很轻松的使用广度优先遍历解决了他。但是越看越熟悉越看越相似使我想起了什么，突然我顿悟了九宫格=八数码。下面就将两个问题我的解决思路分享给大家。如有不妥之地，还请大家及时提出，多多包涵。

在这里插入图片描述

💟九宫格问题💞

💗问题描述💗

题目描述
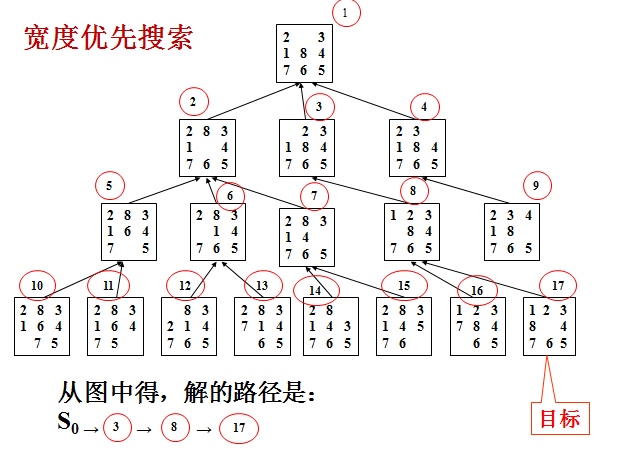
如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。
经过若干次移动，可以形成第二个图所示的局面。
图一：
123
456
78
图二：
123
46
789
我们把第一个图的局面记为：12345678.
把第二个图的局面记为：123.46758
显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。
输入
输入第一行包含九宫的初态，第二行包含九宫的终态。
输出
输出最少的步数，如果不存在方案，则输出-1。
样例输入
12345678.
123.46758
样例输出
3

💗问题分析💗

九宫格，对每个位置的索引进行排序应为123456789
对于某点而言，他的左边右边分别为他自己的索引减一、加一
他上面下面的索引为他自己的索引减三、加三。
移动的时候可以视为每一步移动的都是空白的小格子。将每一步移动之前的格子都保留下来。使用广度优先搜索。
为了防止闭环，我们可以将扫描过的情况加入scaned队列，如果某种情况在scaned或者tempqueue中就不予入队
我认为也就是这一点符合了启发式式搜索的基本概念。

💗代码实现💗

import copy

# 初始位置
n1=list(input())

# 目标串
n2=list(input())

# 存储最终结果
ans=0
flag=True
# 扫描过的情况
scaned=[]
# 队列，用于保存临时列表状态。
tempqueue=[]
tempqueue.append([n1,ans])
while tempqueue:
    temp=tempqueue.pop(0)
    t,ans=temp[0],temp[1]
    scaned.append(t)
    index=t.index('.')
    # 向上移
    if index//3==0:
        pass
    else:
        t1=copy.copy(t)
        t1[index],t1[index-3]=t1[index-3],t1[index]
        if t1 not in scaned and t1 not in [i[0] for i in tempqueue]:
            tempqueue.append([t1,ans+1])
        if t1==n2:
            print(ans+1)
            flag=False
            break
    # 向下移
    if index//3==2:
        pass
    else:
        t1=copy.copy(t)
        t1[index],t1[index+3]=t1[index+3],t1[index]
        if t1 not in scaned and t1 not in [i[0] for i in tempqueue]:
            tempqueue.append([t1,ans+1])
        if t1==n2:
            print(ans+1)
            flag=False
            break
    # 向左移
    if index%3==0:
        pass
    else:
        t1=copy.copy(t)
        t1[index],t1[index-1]=t1[index-1],t1[index]
        if t1 not in scaned and t1 not in [i[0] for i in tempqueue]:
            tempqueue.append([t1,ans+1])
        if t1==n2:
            print(ans+1)
            flag=False
            break
    # 向右移
    if index%3==2:
        pass
    else:
        t1=copy.copy(t)
        t1[index],t1[index+1]=t1[index+1],t1[index]
        if t1 not in scaned and t1 not in [i[0] for i in tempqueue]:
            tempqueue.append([t1,ans+1])
        if t1==n2:
            print(ans+1)
            flag=False
            break
if flag:
    print(-1)

💟八数码-带路径💞

💙问题描述💙

与上述一样，只不过本次打印出了移动的路径

💙问题分析💙

主体与上述分析一样，只不过这次将该情况之前的路径加了进去（方便最后打印）

💙代码实现💙

import copy
# 最终判断是否找到了路径（如果没有找到最后打印-1）
flag=True
# 扫描过的队列
scaned=[]
# 队列，用于保存临时列表状态。
tempqueue=[]

# 判断当前情况是否需要入队（n1实际是一个字符列表）
# scaned 是记录的是扫描过的情况
# [i[0] for i in tempqueue]是仍在队列中的情况
# 这么做的目的就是防止形成环路陷入死循环。
def JudgeStrList(t1):
    if t1[0] not in scaned and t1[0] not in [i[0] for i in tempqueue]:
        tempqueue.append(t1)

def PrintRoute(n1,n2):
        temp=''' | |\n V V\n  V '''
        if n1[0]==n2:
            n1[1].append(n1[0])
            print("到达指定的目标需要移动",len(n1[1]),"次！")
            print("移动路径如下：")
            flag=False
            for i in n1[1]:
                if not flag:
                    flag=True
                else:
                    print(temp)
                for j in range(9):
                    print(i[j],end=" ")
                    if j%3==2:
                        print()
            return True
        return False


# 初始位置
n1=list(input())

# 目标串
n2=list(input())

tempqueue.append([n1,[]])
while tempqueue:
    # print(tempqueue)
    temp=tempqueue.pop(0)
    scaned.append(temp[0])
    index=temp[0].index('.')
    # print(index)
    # 向上移
    if index//3==0:
        pass
    else:
        t1=copy.deepcopy(temp)
        t1[0][index],t1[0][index-3]=t1[0][index-3],t1[0][index]
        t1[1].append(temp[0])
        JudgeStrList(t1) 
        if PrintRoute(t1,n2):
            flag=False
            break
    # 向下移
    if index//3==2:
        pass
    else:
        t1=copy.deepcopy(temp)
        t1[0][index],t1[0][index+3]=t1[0][index+3],t1[0][index]
        t1[1].append(temp[0])
        JudgeStrList(t1) 
        if PrintRoute(t1,n2):
            flag=False
            break
    # 向左移
    if index%3==0:
        pass
    else:
        t1=copy.deepcopy(temp)
        t1[0][index],t1[0][index-1]=t1[0][index-1],t1[0][index]
        t1[1].append(temp[0])
        JudgeStrList(t1) 
        if PrintRoute(t1,n2):
            flag=False
            break
    # 向右移
    if index%3==2:
        pass
    else:
        t1=copy.deepcopy(temp)
        t1[0][index],t1[0][index+1]=t1[0][index+1],t1[0][index]
        t1[1].append(temp[0])
        JudgeStrList(t1) 
        if PrintRoute(t1,n2):
            flag=False
            break
if flag:
    print(-1)

💟有解无解判断💞

在以上两个例子中，直接进行了搜索，如果最后搜索不到的话就打印-1。对于无解的情况搜索量极大可能需要耗费大量的时间。我们可以利用线性代数的一些概念先进行有解无解的判断，然后再进行搜索。这样在某种情况下可以节约大量的时间

如果此初始状态的数列(矩阵)的逆序数与目标状态的数列(矩阵)的逆序数的奇偶性一样，则此问题有解。
逆序数的定义：

有一个数列，在这个数列中任意取一对数字(两个数字)，其两个数字在数列中的(从前到后)
顺序与数字数值的大小相反，称其为一个逆序。这个数列中所有的逆序的和为逆序数。

💟总结💞

八数码问题就是典型的广度优先搜索,博主代码写的比较啰嗦大家可能看不是很懂。一定要记住不变的本质,每次搜索前先将该情况的所有下一个状态保存，然后在对下一个状态逐个进行搜索。为了避免形成闭环（也就是同一状态重复搜索）我们需要再建立一个数组存放遍历过的状态。然后就是按部就班的搜索了。如果需要打印路径的话，博主想的是对每一种状态的之前的状态进行保留（存进列表）。肯定有更好的方法，欢迎大家评论区留言呀。

在这里插入图片描述