背景
给定一棵树中的某一个节点,让你找出这个节点的先序遍历的直接前驱,如果是一颗普通的树,因为指向的单向性,你只能建立两个指针pre,cur_node,pre紧接在cur_node的后面,从头遍历到尾,如果cur_node指向了要找的节点,那么pre就是要找的节点的直接前驱。
可以看到,无论给定的节点在哪里,都需要从根节点开始从头遍历,所以效率是非常低的。
节点的定义
class TreeNode:
def __init__(self, val=None, left=None, right=None, ltag=0, rtag=0):
self.val = val # 值
self.left = left # 左孩子
self.right = right # 右孩子
self.ltag = ltag # 初始值为0 为0说明指向左孩子,为1说明指向直接前驱
self.rtag = rtag # 初始值为0 为0说明指向右孩子,为1说明指向直接后继
构建一颗树
# 创建一颗二叉树(层次遍历)
def create_tree(li):
if not li: return TreeNode()
root = TreeNode(li[0])
cur_que = deque()
cur_que.append(root)
li = li[1:][::-1]
while len(cur_que):
cur_node = cur_que.popleft()
if li:
cur_node.left = TreeNode(li.pop())
cur_que.append(cur_node.left)
if li:
cur_node.right = TreeNode(li.pop())
cur_que.append(cur_node.right)
return root先序遍历线索化
# 先序遍历
def travel(root):
if root:
vist(root)
global pre
pre = root # 更新前驱
if root.ltag == 0: # 如果是左孩子就访问
travel(root.left)
if root.rtag == 0: # 如果是右孩子就访问
travel(root.right)线索化的核心
# 访问当前节点
def vist(cur_node):
global pre
if pre:
if not cur_node.left: # 当前节点没有左孩子,且前驱pre不为空
cur_node.left = pre # 指向它的直接前驱
cur_node.ltag = 1 # 标记当前左指针指向的是直接前驱
if not pre.right and cur_node: # pre没有右孩子 且cur_node不为空
pre.right = cur_node # cur_node就是pre的直接后继
pre.rtag = 1 # 标记当前右指针指向的是直接后继测试
# 线索化
def thread_tree(root):
global pre # 设为全局变量 一开始指向None
pre = None
travel(root)
return root
if __name__ == '__main__':
root = create_tree(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
thread_tree(root)这里使用Tutor进行了运行过程的可视化,最终结果如下(符合预期):
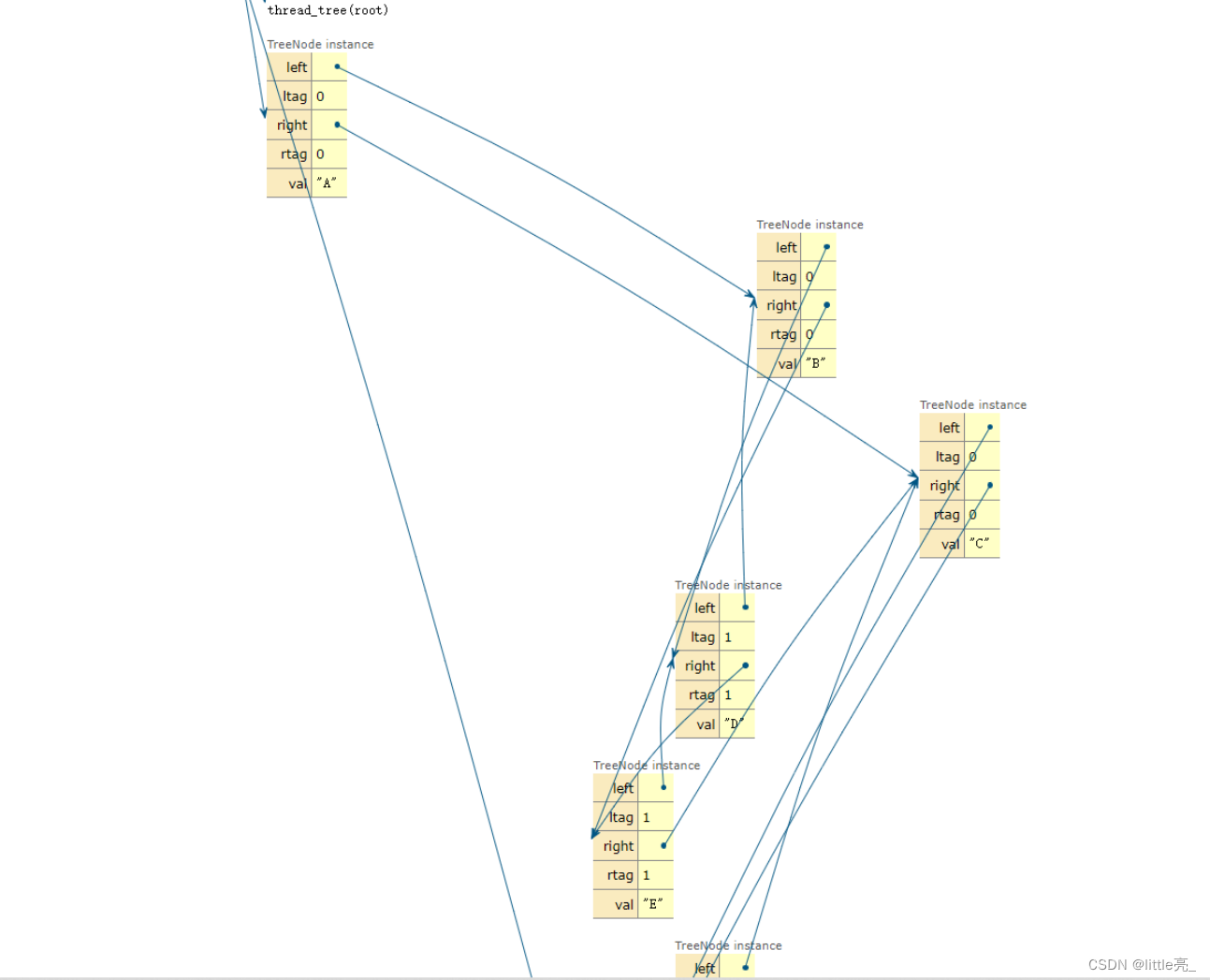

同步更新于个人博客系统:python实现线索二叉树(以先序线索化为例)
源码
# -*- coding: UTF-8 -*-
'''
*****************LLL*********************
* @Project :leetcode
* @File :lll97_二叉树的线索化.py
* @IDE :PyCharm
* @Author :LLL
* @Date :2022/5/16 10:30
*****************************************
'''
from collections import deque
class TreeNode:
def __init__(self, val=None, left=None, right=None, ltag=0, rtag=0):
self.val = val # 值
self.left = left # 左孩子
self.right = right # 右孩子
self.ltag = ltag # 初始值为0 为0说明指向左孩子,为1说明指向直接前驱
self.rtag = rtag # 初始值为0 为0说明指向右孩子,为1说明指向直接后继
# 创建一颗二叉树(层次遍历)
def create_tree(li):
if not li: return TreeNode()
root = TreeNode(li[0])
cur_que = deque()
cur_que.append(root)
li = li[1:][::-1]
while len(cur_que):
cur_node = cur_que.popleft()
if li:
cur_node.left = TreeNode(li.pop())
cur_que.append(cur_node.left)
if li:
cur_node.right = TreeNode(li.pop())
cur_que.append(cur_node.right)
return root
# 访问当前节点
def vist(cur_node):
global pre
if pre:
if not cur_node.left: # 当前节点没有左孩子,且前驱pre不为空
cur_node.left = pre # 指向它的直接前驱
cur_node.ltag = 1 # 标记当前左指针指向的是直接前驱
if not pre.right and cur_node: # pre没有右孩子 且cur_node不为空
pre.right = cur_node # cur_node就是pre的直接后继
pre.rtag = 1 # 标记当前右指针指向的是直接后继
# 先序遍历
def travel(root):
if root:
vist(root)
global pre
pre = root # 更新前驱 pre总是等于上一轮的root
if root.ltag == 0: # 如果是左孩子就访问
travel(root.left)
if root.rtag == 0: # 如果是右孩子就访问
travel(root.right)
# 线索化
def thread_tree(root):
global pre # 设为全局变量 一开始指向None
pre = None
travel(root)
return root
if __name__ == '__main__':
root = create_tree(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
thread_tree(root)
