1.特征工程是什么？

数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢？顾名思义，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。

2.数据漏斗

2.1数据漏斗解决的问题

1.不属于同一量纲：即特征的规格不一样，不能够放在一起比较。
2.信息冗余：对于某些定量特征，其包含的有效信息为区间划分。
3.存在缺失值或者异常值。
4.其他非共性的信息问题。

2.2解决不属于同一量纲的问题

常用的有归一化（有的教材说是区间缩放法）和标准化，他们都在包sklearn.preprocessing里面。

归一化（区间缩放法）

他在sklearn.preprocessing的MinMaxScaler中
数学表达式：
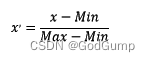
在这里插入图片描述
代码示例：

from sklearn.preprocessing import MinMaxScaler
#区间缩放，返回值为缩放到[0, 1]区间的数据
MinMaxScaler().fit_transform(iris.data)

标准化

他在sklearn.preprocessing的StandardScaler中
数学表达式：
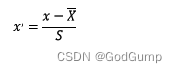
在这里插入图片描述
代码示例：

from sklearn.preprocessing import StandardScaler
#标准化，返回值为标准化后的数据
StandardScaler().fit_transform(iris.data)

使用建议：归一化对异常值很敏感，因此一般情况下使用标准化会更好。

2.3解决信息冗余的问题

由于IRIS数据集的特征皆为定量特征，故使用其目标值进行哑编码（实际上是不需要的）。

from sklearn.preprocessing import OneHotEncoder
from sklearn.datasets import load_iris
#哑编码，对IRIS数据集的目标值，返回值为哑编码后的数据
iris = load_iris(return_X_y=False)
iris.target = OneHotEncoder(sparse=False).fit_transform(iris.target.reshape(-1,1))
iris.target

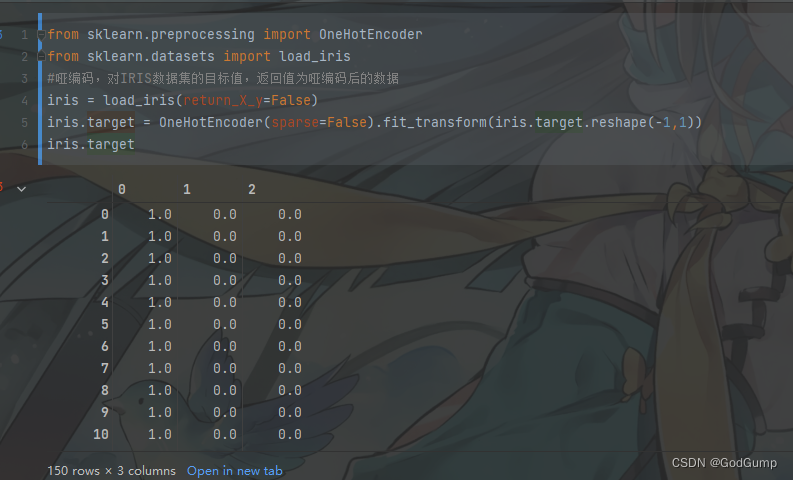
在这里插入图片描述

2.4解决缺失值问题

由于IRIS数据集没有缺失值，故对数据集新增一个样本，4个特征均赋值为NaN，表示数据缺失。
这个因情况而定，有的使用的是平均数，有的使用的是中位数，当然还有别的。

3.特征选择

数据漏斗结束后，就需要进行特征选择。有人可能会说，博主你刚刚不是才说数据和特征决定了机器学习的上限嘛？怎么又改口了。数量多的同时，质量也很重要，过多的无用特征很容易导致过拟合的问题。
一般特征选择会从发散性和相关性考虑。通过选择方式的不同又可以将选择方法分为3种。

3.1Filter（阈值过滤法）

3.1.1 方差选择法

使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。样式代码如下：

from sklearn.feature_selection import VarianceThreshold
#方差选择法，返回值为特征选择后的数据
#参数threshold为方差的阈值
iris.data = VarianceThreshold(threshold=2).fit_transform(iris.data)
iris.data

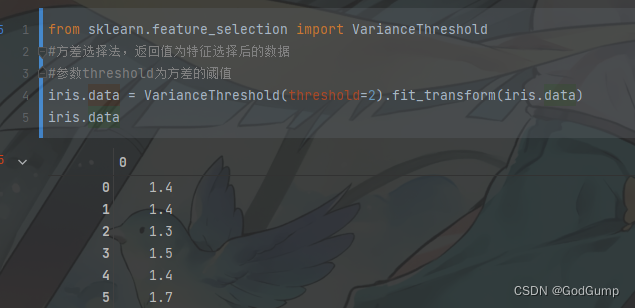
在这里插入图片描述

3.1.2 相关系数法

使用相关系数法，先要计算各个特征对目标值的相关系数以及相关系数的P值。用feature_selection库的SelectKBest类结合相关系数来选择特征。

3.1.3 卡方检验

经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：
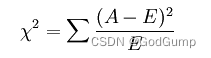
在这里插入图片描述
这个统计量的含义简而言之就是自变量对因变量的相关性。用feature_selection库的SelectKBest类结合卡方检验来选择特征。

3.2 Wrapper（包装法）

根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。最常用的是逻辑回归中的递归特征消除法（RFE）：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
# #参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

3.3 Embedded

3.3.1 使用带惩罚项的基模型

除了筛选出特征外，同时也进行了降维。惩罚项一般使用L2（当然也有L1）
示例代码（）：

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

 #逻辑回归默认L2，可以通过修改参数penalty
SelectFromModel(LogisticRegression(C=0.1)).fit_transform(iris.data, iris.target)

3.3.2 基于树模型的特征选择法

这个和3.3.1大同小异，只是换了调用。

4 . 特征降维

4.1 主成分分析法（PCA）

主成分分析算法（PCA）是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留住较多的原数据点的特性。
示例代码：

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
print(pca.components_)
print(pca.explained_variance_)

4.2 线性判别分析法（LDA）

LDA的全称是Linear Discriminant Analysis（线性判别分析），是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant。
LDA的原理是，将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：
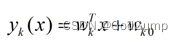
在这里插入图片描述
代码将上面的PCA换LDA即可