[Python知识库]傅里叶变换——使用 python 进行周期信号和非周期信号的傅里叶变换；如何理解傅里叶变换后的频谱是连续还是离散的问题

参考资料

• 基波与谐波

• 如何使用 python 实现快速的傅里叶变换

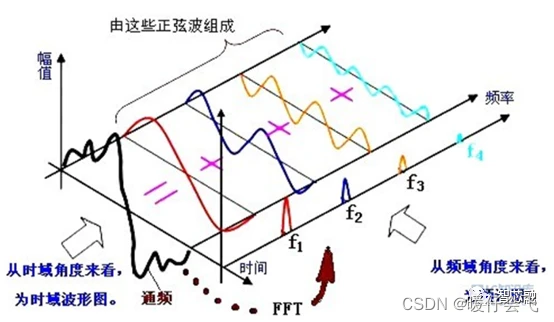
  • 首先对信号进行 scipy 中的 fft 变换，得到和原始信号相同长度的变换结果 fft_y, 这个结果包含振幅和相位信息
  • 变换得到的结果包含相位谱和振幅谱，通过 abs(fft_y) 可以直接得到变换后结果的"双边"振幅谱；通过np.angle(fft_y) 可以直接得到”双边“相位谱
  • 将振幅和相位谱分别取一半就得到了半边的频谱
  • 也可以对得到的频谱进行归一化，归一化的方式就是除以 len(fft_y) ，具体操作可以在上面的文章中得到详细答案

• 或者直接采用 scipy 中的 rfft 和 rfftfreq 来得到半边的频谱（因为傅里叶变换后的频谱都是对称的）；具体代码实现可以参考这篇文章

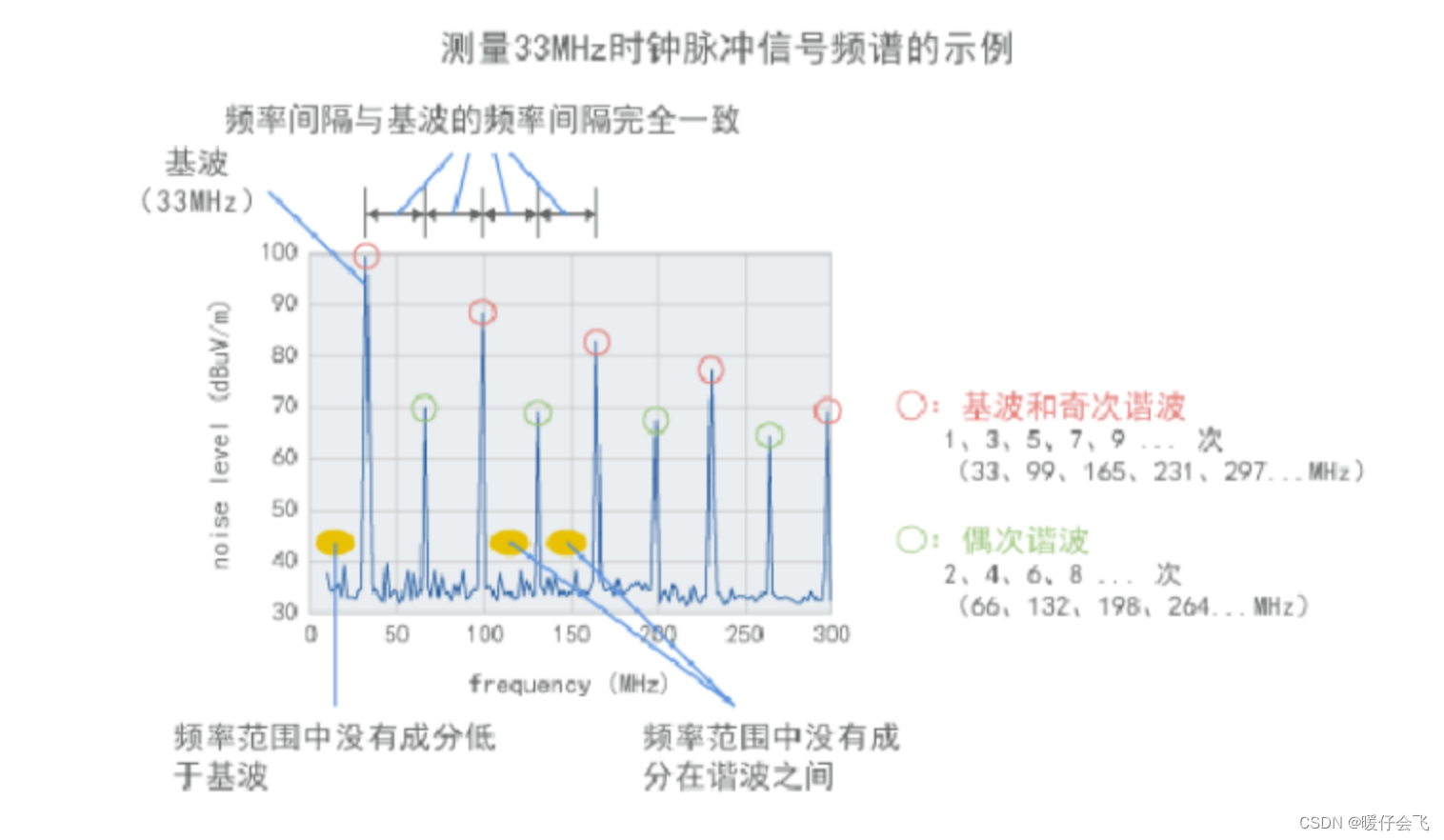
• 奇次谐波与偶次谐波：

  • 假设要进行傅里叶分解的信号频率是 $w$，那么经过傅里叶分解之后，频谱图上频率也为 $w$ 所代表的正弦波称为这个信号的 ”基波“
  • 类似的，经过傅里叶分解之后频谱图上频率处在 $w$ 奇数倍所代表的的波称为奇次谐波，例如波的频率分别是 $3w,5w,7w$ 所代表的的波
  • $w$ 偶数倍所代表的的波称为偶次谐波，例如波的频率分别是 $2w,4w,6w$ 所代表的波。
    图片来源

• 谐波及其危害

• 如何理解周期信号的傅里叶变换在频域上是离散的，而非周期信号经过傅里叶变换后的频域信号是连续的
  

  • 图片来源

• 傅里叶变换的意义，以及如何理解非周期信号的傅里叶变换（将其看成在 -$\infty ,+\infty$ 上的周期信号）

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系