Python系列文章目录
第一章 Python 入门
第二章 Python基本概念
第三章 序列
第四章 控制语句
第五章 函数
函数
前言
在本章, 我们将学习Python函数相关知识. 了解其定义和底层原理以及变量作用域: 局部变量和全局变量
然后, 学习函数的五种参数类型: 位置参数, 默认值参数, 命名参数, 可变参数, 强制命名参数
再然后, 学习几种常见函数: 匿名函数, eval 函数, 递归函数, 嵌套参数
最后, 通过几个实操练习来巩固本章所学知识
一、函数是什么
一个程序由一个一个的任务组成;函数就是代表一个任务或者一个功能(function), 是代码复用的通用机制
函数特点
- 函数是可重用的程序代码块. 一个完整的函数应包含: 函数名, 参数, 函数体(代码, 注释)
- 函数的作用,不仅可以实现代码的复用,更能实现代码的一致性。
一致性指的是,只要修改函数的代码,则所有调用该函数的地方都能得到体现 - 在编写函数时,函数体中的代码写法和我们前面讲述的基本一致,只是对代码实现了封装,并增加了函数调用、传递参数、返回计算结果等内容
1. 定义
Python中,定义函数的语法如下:
def 函数名 ([参数列表]) :
"""文档字符串"""
函数体/若干语句
【操作】定义和调用函数
官方建议: 在函数定义前和调用前都应该留两行空行
# 实操代码
def add(a, b, c):
add_result = a + b + c
print("{0}、{1}、{2}三个数的和是:{3}".format(a, b, c, add_result))
return add_result
# 类或者函数定义后只要要有两行空行, 才进行调用或者其他操作(PEP 8: E305)
# 函数的调用
add(10, 20, 30)
add(6, 60, 66)
2. 内存底层分析
Python中,“一切都是对象”。实际上,执行 def 定义函数后,系统就创建了相应的函数对象
-
我们执行如下程序,然后进行解释
# 【操作】测试文档字符串的使用: 定义一个打印n个星号的无返回值的函数 # 三重双引号字符串应该用于文档字符串(Triple double-quoted strings should be used for docstrings) def print_star(n): """ 根据传入的n,打印多个星号 :param n: 传入的数字 :return: n个星号拼接的字符串 """ s = "*" * n print(s) return s # Python中,“一切都是对象”。实际上,执行 def 定义函数后,系统就创建了相应的函数对象。我们执行如下程序,然后进行解释: print(id(print_star)) print(type(print_star)) print(print_star) # 类似对象的赋值一样, 函数也可以赋值. 将原函数的引用复制到另一个对象上. # 赋值后, 新的函数和原来的函数都可以调用 func_print_star = print_star print(id(func_print_star)) # 显然,我们可以看出变量 c 和 print_star 都是指向了同一个函数对象. 因此,执行 func_print_star(3) 和执行print_star(3) 的效果是完全一致的 # Python中,圆括号意味着调用函数. 在没有圆括号的情况下,Python会把函数当做普通对象 func_print_star(3) print_star(3) -
在上述代码使用def 去定义函数时. 在内存中就会创建函数对象, 并且通过变量
print_star来引用它. 如图所示:
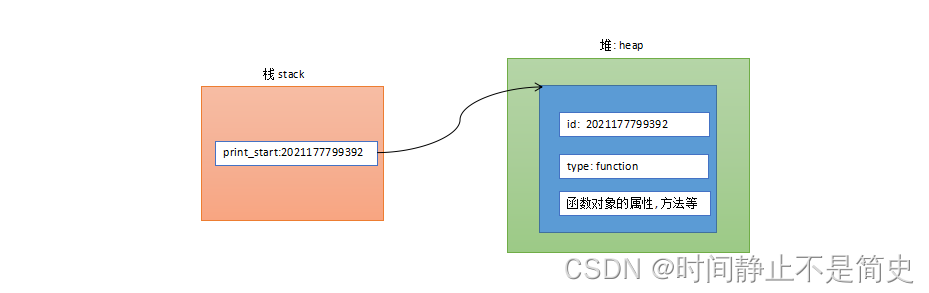
-
在上述代码执行
func_print_star = print_star后, 会将print_star的值(函数的引用) 赋值给func_print_star.
该过程之后的内存图如下:
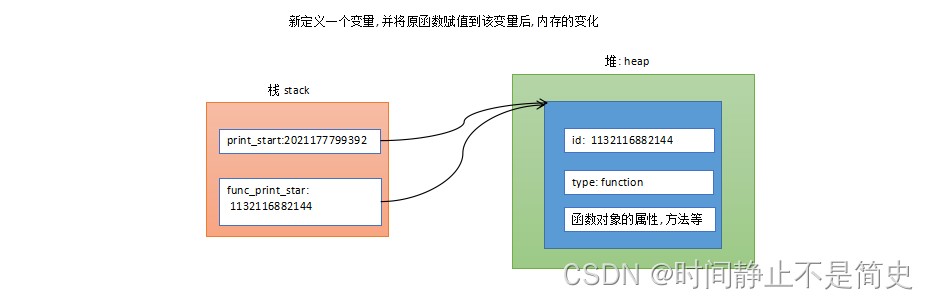
-
可以看出变量 c 和 print_star 都是指向了同一个函数对象。
因此,执行func_print_star(3)和执行print_star(3)的效果是完全一致的
3. 变量的作用域
变量起作用的范围称为变量的作用域,不同作用域内同名变量之间互不影响
变量分为:全局变量、局部变量. 下面来总结下全局变量和局部变量
全局变量:
- 在函数和类定义之外声明的变量. 作用域为定义的模块,从定义位置开始直到模块结束。
- 全局变量降低了函数的通用性和可读性. 应尽量避免全局变量的使用
- 要在函数内改变全局变量的值,使用 global 声明一下
局部变量:
- 在函数体中(包含形式参数)声明的变量
- 局部变量的引用比全局变量快,优先考虑使用
- 如果局部变量和全局变量同名,则在函数内隐藏全局变量,只使用同名的局部变量
【操作】全局变量的作用域测试
注意: 如果要在函数内改变全局变量的值, 增加 global 关键字声明
a = 100 # 全局变量
def fun1():
global a # 如果要在函数内改变全局变量的值, 增加 global 关键字声明
print(a) # 打印全局变量a的值
a = 300
fun1()
print(a)
【操作】 输出局部变量和全局变量
a = 100
def f1(a, b, c,):
print(a, b, c) # 1 2 3
print(locals()) # 打印输出的局部变量 {'a': 1, 'b': 2, 'c': 3}
print("#"*20) # ####################
print(globals()) # 打印输出所有全局变量信息
f1(1, 2, 3)
【操作】 局部变量和全局变量效率测试
def testGlobalVariable():
start = time.time()
global a
for i in range(100000000):
a += 1
end = time.time()
print("耗时:", end-start)
def testLocalVariable():
c = 1000
start = time.time()
for i in range(100000000):
c += 1
end = time.time()
print("耗时:", end-start)
testGlobalVariable() # 耗时: 5.558136940002441
testLocalVariable() # 耗时: 3.769923448562622
注意:
- 局部变量的查询和访问速度比全局变量快,在循环的时候优先考虑使用
- 在特别强调效率的地方或者循环次数较多的地方,可以通过将全局变量转为局部变量提高运行速度
二、参数
我们都应该清楚: 一个完整的函数应包含: 函数名, 参数, 函数体(代码, 注释)
如果把一个函数比作人, 那么函数名就是人名, 函数体是人的身体, 而参数则是人类的灵魂.
1. 参数类型
参数类型介绍
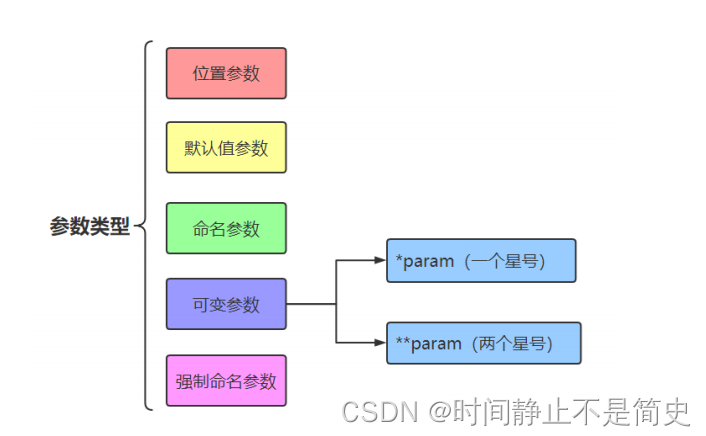
位置参数
函数调用时,实参默认按位置顺序传递,需要个数和形参匹配。
按位置传递的参数,称为:“位置参数”
【操作】测试位置参数
def positionalParameter(a, b, c):
print(a, b, c)
positionalParameter(1, 2, 3)
# positionalParameter(1, 2) # TypeError: positionalParameter() missing 1 required positional argument: 'c'
默认值参数
参数在传递时就是可选的, 称为“默认值参数”。默认值参数放到位置参数后面
在默认值参数无传入时就是用其初始设置的默认值, 有传入时则使用实际参数
【操作】测试默认值参数
def f1(a, b, c=10, d=20): # 默认值参数必须位于普通位置参数后面
print(a, b, c, d)
f1(8, 9) # 8 9 10 20
f1(8, 9, 19) # 8 9 19 20
f1(8, 9, 19, 29) # 8 9 19 29
命名参数
按照形参的名称传递参数,称为“命名参数”,也称“关键字参数
【操作】测试命名参数
def f1(a, b, c):
print(a, b, c)
f1(8, 9, 19) # 位置参数
f1(c=10, a=20, b=30) # 命名参数
可变参数
可变参数指的是“可变数量的参数”。分两种情况:
*param(一个星号),将多个参数收集到一个“元组”对象中**param(两个星号),将多个参数收集到一个“字典”对象中
【操作】测试可变参数处理(元组、字典两种方式)
def variableParameter(a, b, *c):
print(a, b, c)
def variableParameter2(a, b, **c):
print(a, b, c)
def variableParameter3(a, *b, **c):
print(a, b, c)
variableParameter(8, 9, 19, 20) # 8 9 (19, 20) 元组
variableParameter2(8, 9, name='cba', age=66) # 8 9 {'name': 'cba', 'age': 66} 字典
variableParameter3(8, 9, 20, 30, name='cba', age=66) # 8 (9, 20, 30) {'name': 'cba', 'age': 66} 元组+字典
强制命名参数
在带星号的“可变参数”后面增加新的参数,必须在调用的时候“强制命名参数”
【操作】测试强制命名参数
# 在带星号的“可变参数”后面增加新的参数,必须在调用的时候“强制命名参数”
def f1(*a, b, c):
print(a, b, c)
# f1(2, 3, 4) # 会报错.由于a是可变参数, 将2,3,4全部收集。造成b和c没有赋值
f1(2, b=3, c=4)
2. 参数传递
函数的参数传递本质上就是:从实参到形参的赋值操作.
Python中 “一切皆对象”,所有的赋值操作都是“引用的赋值”. 所以,Python中参数的传递都是“引用传递”,不是“值传递”
具体操作时分为两类:
- 对“可变对象”进行“写操作”,直接作用于原对象本身
可变对象包括: 字典、列表、集合、自定义的对象等 - 对“不可变对象”进行“写操作”,会产生一个新的“对象空间”,并用新的值填充这块空间
不可变对象包括: 数字、字符串、元组、function等
传递可变对象的引用
传递参数是可变对象(例如:列表、字典、自定义的其他可变对象等),实际传递的还是对象的引用
在函数体中不创建新的对象拷贝,而是可以直接修改所传递的对象
【操作】参数传递:传递可变对象的引用
b = [10, 20] # 创建并初始化一个列表
def f2(m):
print("m:", id(m)) # b和m是同一个对象
m.append(30) # 由于m是可变对象,不创建对象拷贝,直接修改这个对象
f2(b)
print("b:", id(b))
print(b)

传递不可变对象的引用
传递参数是不可变对象(例如: int 、 float 、字符串、元组、布尔值),实际传递的还是对象的引用
在”赋值操作”时,由于不可变 对象无法修改,系统会新创建一个对象
【操作】参数传递:传递不可变对象的引用
a = 100
def f1(n):
print("n:", id(n)) # 传递进来的是a对象 n: 2296286416208
n = n + 200 # 由于a是不可变对象, 因此创建新的对象n
print("n:", id(n)) # n已经变成了新的对象 n: 2296287459216
print(n) # 300
# 通过 id 值我们可以看到 n 和 a 一开始是同一个对象。给n赋值后,n是新的对象
f1(a)
print("a:", id(a)) # a: 2296286416208
浅拷贝和深拷贝
- 浅拷贝:拷贝对象,但不拷贝子对象的内容,只是拷贝子对象的引用, 对子对象的修改会影响源对象
- 深拷贝:拷贝对象,并且会连子对象的内存也全部(递归)拷贝一份,对子对象的修改不会影响源对象
【操作】测试浅拷贝和深拷贝
import copy
def testShadowCopy():
"""测试浅拷贝: 浅拷贝后进行操作, 会导致子对象的变化, 但不会影响子对象内存变化"""
a = [10, 20, [30, 40]]
b = copy.copy(a)
print("a", a) # a [10, 20, [30, 40]]
print("b", b) # b [10, 20, [30, 40]]
b.append(50)
b[2].append(60)
print("浅拷贝")
print("a", a) # a [10, 20, [30, 40, 60]]
print("b", b) # b [10, 20, [30, 40, 60], 50]
def testDeepCopy():
"""测试深拷贝: 深拷贝后进行操作, 不会影响原来对象的变化"""
a = [10, 20, [30, 40]]
b = copy.deepcopy(a)
print("a", a) # a [10, 20, [30, 40]]
print("b", b) # b [10, 20, [30, 40]]
b.append(50)
b[2].append(60)
print("深拷贝")
print("a", a) # a [10, 20, [30, 40]]
print("b", b) # b [10, 20, [30, 40, 60], 50]
testShadowCopy()
print("============================")
testDeepCopy()
传递不可变对象包含的子对象是可变的情况
传递不可变对象时, 不可变对象里面包含的子对象是可变的.
若方法内修改了这个可变对象,源对象也发生了变化
【操作】测试传递不可变对象包含的子对象是可变的情况
a = (10, 20, [5, 6]) # 声明一个元组(不可变), 元组里面包含一个列表(可变)
print("a:", id(a)) # a: 2106990123072
def testImmutableObject(m):
print("m:", id(m)) # m: 2106990123072
m[2][0] = 888
print(m) # (10, 20, [888, 6])
print("m:", id(m)) # m: 2106990123072 从这里可以看出对象值改变, 但是引用没有变化, 因此可以断定是源对象发生了变化
testImmutableObject(a)
print(a) # (10, 20, [888, 6])
三、常见函数
lambda表达式和匿名函数
lambda 表达式可以用来声明匿名函数, 是一种简单的、在同一行中定义函数的方法
lambda 函数实际生成了一个函数对象
lambda 表达式的基本语法如下:
lambda arg1,arg2,arg3... : <表达式>
【操作】测试lambda表达式
f = lambda a, b, c: a + b + c
print(f)
print(f(2, 3, 4))
g = [lambda a: a * 2, lambda b: b * 3, lambda c: c * 4]
print((g[0](1), g[1](7), g[2](8))) # 在列表的每个位置上进行赋值然后分别进行运算后输出

eval()函数
将字符串 str 当成有效的表达式来求值并返回计算结果。
语法格式:
eval(source[, globals[, locals]]) -> value
# 参数
# source :一个Python表达式或函数 compile() 返回的代码对象
# globals :可选。必须是 dictionary
# locals :可选。任意映射对象
【操作】测试eval()函数
s = "print('abcde')"
eval(s) # abcde
a = 10
b = 20
c = eval("a+b")
print(c) # 30
dict1 = dict(a=100, b=200)
d = eval("a+b", dict1)
print(d) # 300
注意:
eval函数会将字符串当做语句来执行,因此存在被注入安全隐患.
比如:字符串中含有删除文件的语句. 因此使用时候要慎重!!!
递归函数
递归(recursion)是一种常见的算法思路,在很多算法中都会用到. 比如:深度优先搜索(DFS:Depth First Search)等.
递归的基本思想就是“自己调用自己”. 每个递归函数必须包含两个部分:
- 终止条件: 表示递归什么时候结束. 一般用于返回值,不再调用自己
- 递归步骤: 把第n步的值和第n-1步相关联。
递归函数由于会创建大量的函数对象、过量的消耗内存和运算能力. 在处理大量数据时,谨慎使用
【操作】测试递归函数
def testRecursion(m):
print("start m:", m)
if m == 1:
print("recursion over")
else:
testRecursion(m - 1)
print("end m:", m - 1)
testRecursion(3)
"""打印结果
start m: 3
start m: 2
start m: 1
recursion over
end m: 1
end m: 2
"""
嵌套函数(内部函数)
嵌套函数就是在函数内部定义的函数
使用场景
- 封装 - 数据隐藏. 外部无法访问“嵌套函数”
- 嵌套函数,可以让我们在函数内部避免重复代码
- 闭包
语法格式举例
在程序中, inner() 就是定义在 outer() 函数内部的函数. inner() 的定义和调用都在 outer() 函数内部
def outer():
print("execute outer...")
def inner():
print("execute inner...")
inner()
outer()
【操作】使用嵌套函数避免重复代码
def printChineseName(name, familyName):
print("{0} {1}".format(familyName, name))
def printEnglishName(name, familyName):
print("{0} {1}".format(name, familyName))
# 使用1个函数代替上面的两个函数
def testPrintName(isChinese, name, familyName):
def printName(name_1, name_2):
print("{0} {1}".format(name_1, name_2))
if isChinese:
printName(familyName, name)
else:
printName(name, familyName)
testPrintName(True, "唐纳德", "特朗普") # 特朗普 唐纳德
testPrintName(False, "唐纳德", "特朗普") # 唐纳德 特朗普
nonlocal关键字
nonlocal 用来在内层函数中,声明外层函数的局部变量
global 函数内声明全局变量,然后才使用全局变量
之间的关系如图所示
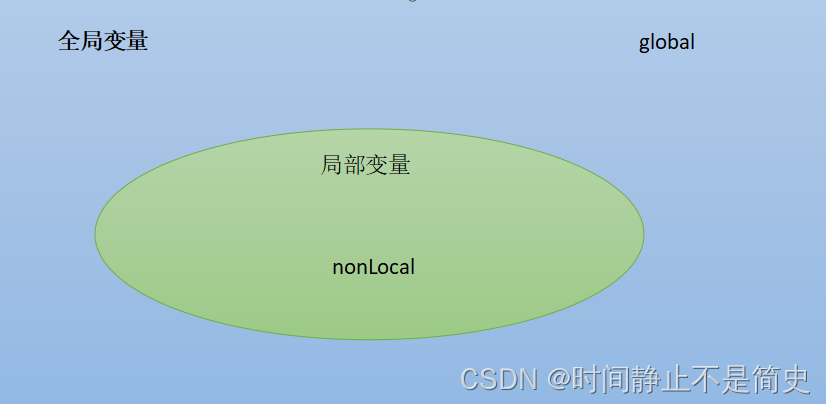
【操作】测试nonlocal、global关键字的用法
a = 100
def outer():
b = 10
def inner():
nonlocal b # 声明外部函数的局部变量
print("inner b:", b)
b = 20
global a
a = 1000
inner()
print("after execute inner, outer b :", b)
outer()
print("a:", a)
print("b:", b)
"""
inner b: 10
after execute inner, outer b : 20
a: 1000
b: 20
"""
LEGB规则
Python在查找变量“名称”时,是按照LEGB规则查找的:
- Local 指的就是函数或者类的方法内部
- Enclosed 指的是嵌套函数(一个函数包裹另一个函数,闭包)
- Global 指的是模块中的全局变量
- Built in 指的是Python为自己保留的特殊名称
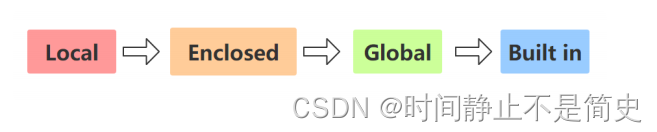
LEGB查询过程:
- 如果某个 name 映射在局部 local 命名空间中没有找到,
- 接下来就会在闭包作用域 enclosed 进行搜索,
- 如果闭包作用域也没有找到,Python就会到全局 global 命名空间中进行查找,
- 最后会在内建built-in 命名空间搜索 (如果一个名称在所有命名空间中都没有找到,就会产生一个 NameError )
【操作】测试LEGB
从内到外依次将几个 s 注释掉,观察控制台打印的内容,体会LEBG的搜索顺序
s = "global"
def outer():
s = "outer"
def inner():
s = "inner"
print(s)
inner()
outer()
四、实操作业
-
定义一个函数实现反响输出一个整数。比如:输入3245,输出5432.
-
编写一个函数,计算下面的数列:

-
输入三角形三个顶点的坐标,若有效则计算三角形的面积;如坐
标无效,则给出提示 -
输入一个毫秒数,将该数字换算成小时数,分钟数、秒数
-
使用海龟绘图。输入多个点,将这些点都两两相连
问题答案分割线
问题1:
- 核心: 如何将输入的值进行反转
- 解决思路(之一): 利用列表的特性, 将输入的数字转换成 str, 然后转换成列表, 反转后遍历该列表然后放入一个变量中, 最后输出的时候再转成数字即可
- 解题代码
# 定义一个函数实现反响输出一个整数。比如:输入3245,输出5432
def printIntNumReverse(intNum):
a = list(str(intNum))
a.reverse()
b = ""
for i in a:
b += i
return int(b)
print(printIntNumReverse(3245))
问题2:
- 核心: 考察递归函数的使用
- 解题思路: n = 0 的这种条件应该单独列出, 其实这里默认 n >=0. 当然如果想要代码更健壮应该考虑 n < 0 的情况
- 解题代码
# 编写一个函数,计算下面的数列:
def mn(n):
if n == 0:
total = 0
else:
total = (1-(1/(n+1))+mn(n-1)
return total
print(mn(2))
问题3
- 核心: 考察三角形相关法则(三边关系, 面积计算式) 以及 后台如何记录录入的坐标
- 解题思路:
1)录入坐标 (利用 map 将输入的字符串转换成坐标 )
2)计算三边长
3)校验是否能够构成三角形(三边关系)
4)利用面积公式变形计算三角形面积 - 解题代码:
# 输入三角形三个顶点的坐标,若有效则计算三角形的面积;如坐标无效,则给出提示
import math
def isvalid(a=0.0, b=0.0, c=0.0):
"""判断三条边长是否符合三角形的定义:任意两边之和大于第三边或者任意两边之差小于第三边"""
side = [a, b, c]
side.sort()
if side[0] + side[1] > side[2] or side[2] - side[1] < side[0]:
return True
else:
return False
def calculate_area():
"""获取三角形的三个顶点坐标并计算该三角形的面积"""
x1, y1 = map(int, input('请输入第一个顶点坐标:').split())
x2, y2 = map(int, input('请输入第二个顶点坐标:').split())
x3, y3 = map(int, input('请输入第三个顶点坐标:').split())
# 计算三条边长
side1 = math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
side2 = math.sqrt((x1 - x3) ** 2 + (y1 - y3) ** 2)
side3 = math.sqrt((x2 - x3) ** 2 + (y2 - y3) ** 2)
# 调用 isvalid() 函数,判断是否能够构成三角形
if isvalid(side1, side2, side3):
# 计算半周长
s = (side1 + side2 + side3) / 2
# 计算面积
area = (s * (s - side1) * (s - side2) * (s - side3)) ** 0.5
print('三角形的面积为:{:.2f}'.format(area))
else:
print('坐标无效,无法构成三角形')
calculate_area()
问题4
- 核心: 利用 round 函数, 并且清楚时间单位之间的转换关系
- 解题思路: 将输入的毫秒数转成int , 然后按照时间单位之间的换算关系进行换算即可.
- 解题代码:
# 输入一个毫秒数,将该数字换算成小时数,分钟数、秒数
def TimeConverter():
ms = int(input('请输入毫秒数:')) # 保留两位小数,但若ms太小,h就会显示为0。
s = round(ms / 1000, 2)
m = round(s / 60, 2)
h = round(m / 60, 2)
print('{0}换算后等于{1}秒,等于{2}分钟,等于{3}小时'.format(ms, s, m, h))
TimeConverter()
