主成分分析
理论
主成分分析(Principal Component Analysis,PCA)是一种多变量统计方法,它是最常用的降维方法之一,通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量,转换后的变量被称为主成分。
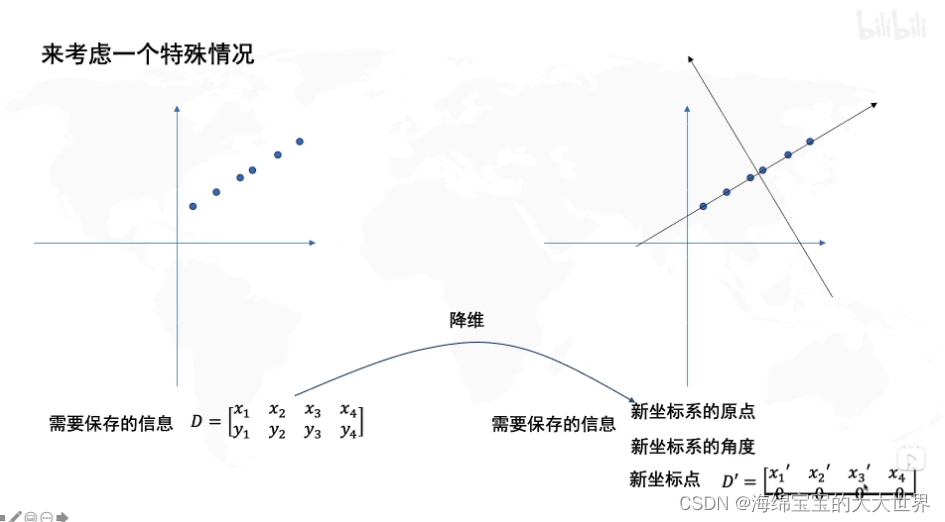
PCA的实质就是:找到一个新的坐标系,使得数据保存少维数时,信息损失最少(保留信息最多)。用比原数据少的维数来表达原数据,将主要的维度提取出来表现整体数据。
-
坐标系第一个维度:主成分一
-
坐标系第二个维度:主成分二
-
找到数据在主成分一、主成分二上边投影分布方差最大,保存的信息是最多的(投影方差越大,说明越分散,越分散概率就越小,概率越小说明信息量就越大)。
步骤
首先:去中心化(将坐标原点放到数据中心)
其次:找到坐标系(就是在找新坐标下的角度,方差最大的方向)
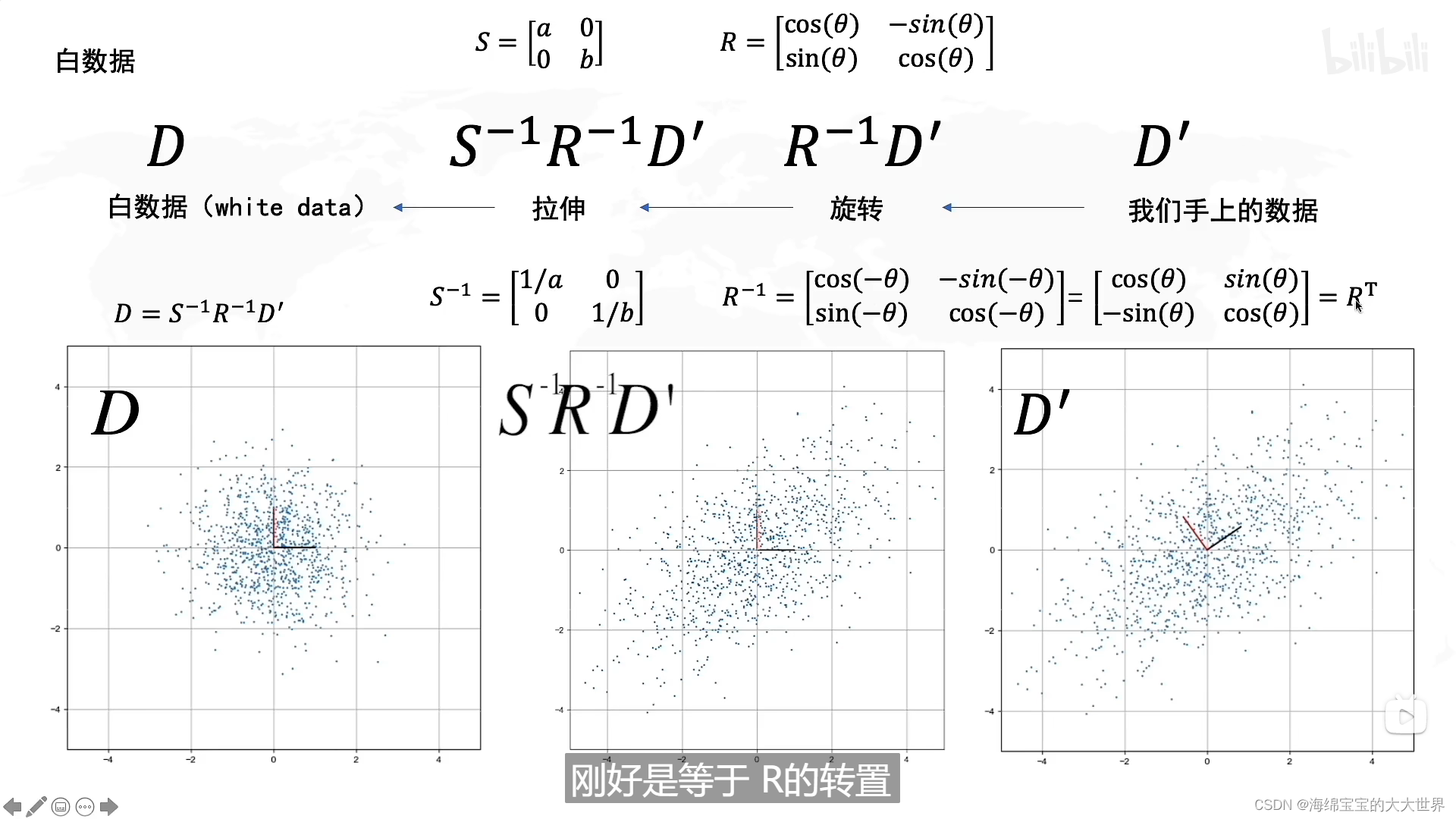
其中D‘是我们要降维的数据,D‘是XY两维相关的,X方向变大的时候,Y也会变大,D是我们的目标,做成XY互不相关的。
-
拉伸的方向就是方差最大的方向
-
R旋转的角度决定了我们方差最大方向,R就是我们要算的,也就是坐标系旋转角度,求出了R,PCA也就解决了。
-
R的本质:协方差矩阵的特征向量就是R
-
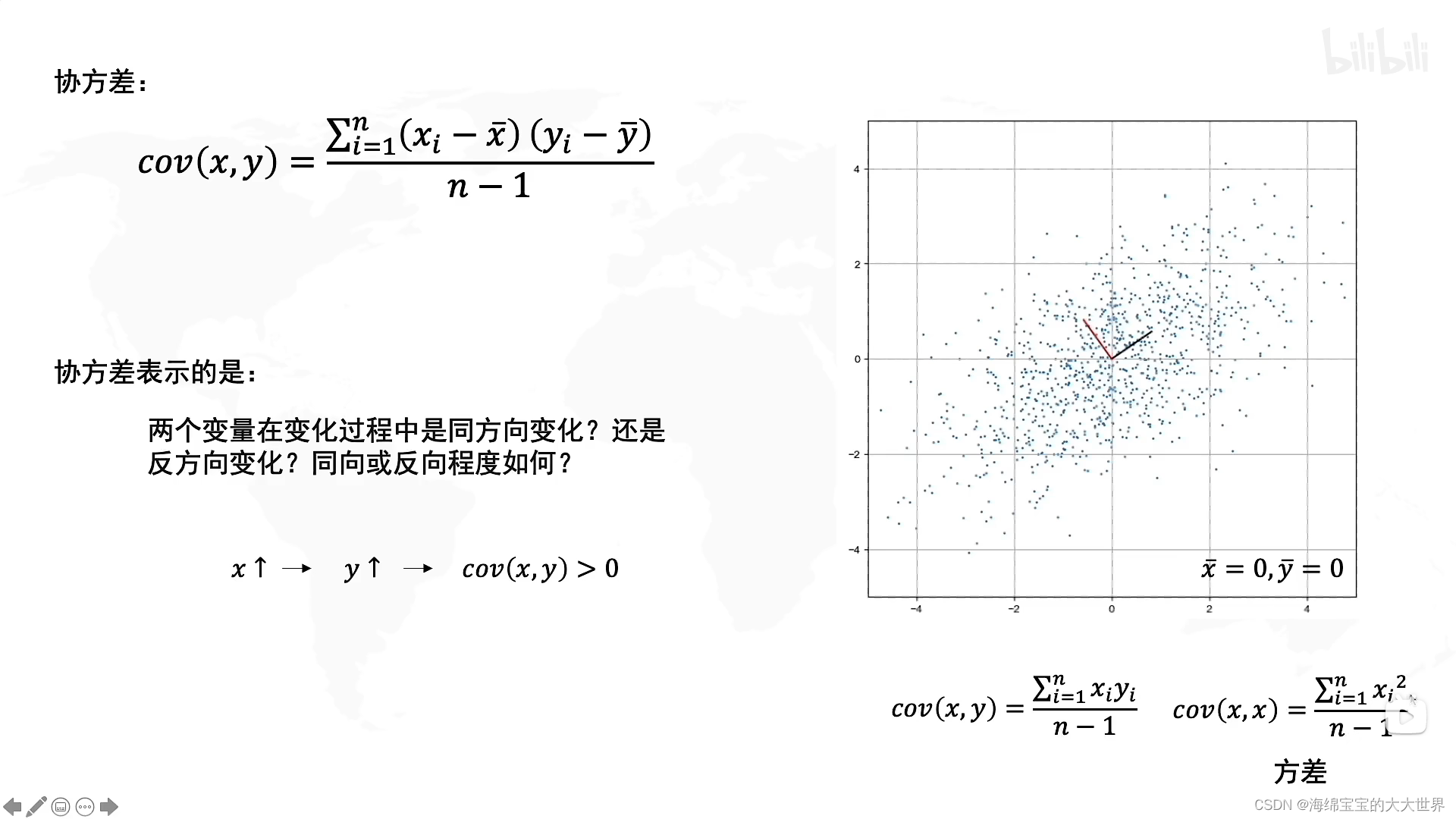
单调递增协方差大于0,反之。
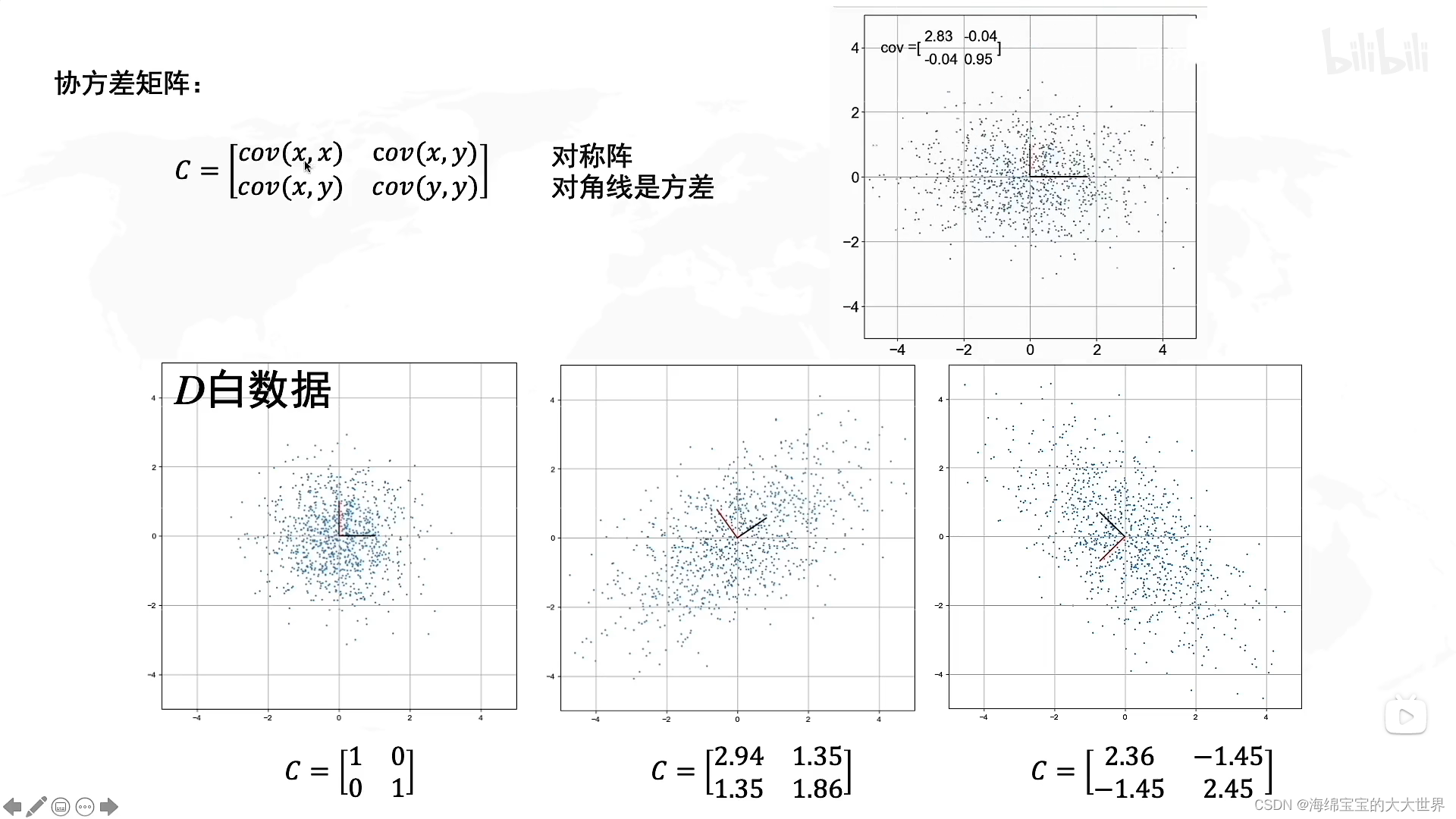
协方差其意义: 度量各个维度偏离其均值的程度。协方差的值如果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),结果为负值就说明负相关的,如果为0,也是就是统计上说的“相互独立”。 -
如果XY是不相关的,那么协方差cov(x,y)就为0

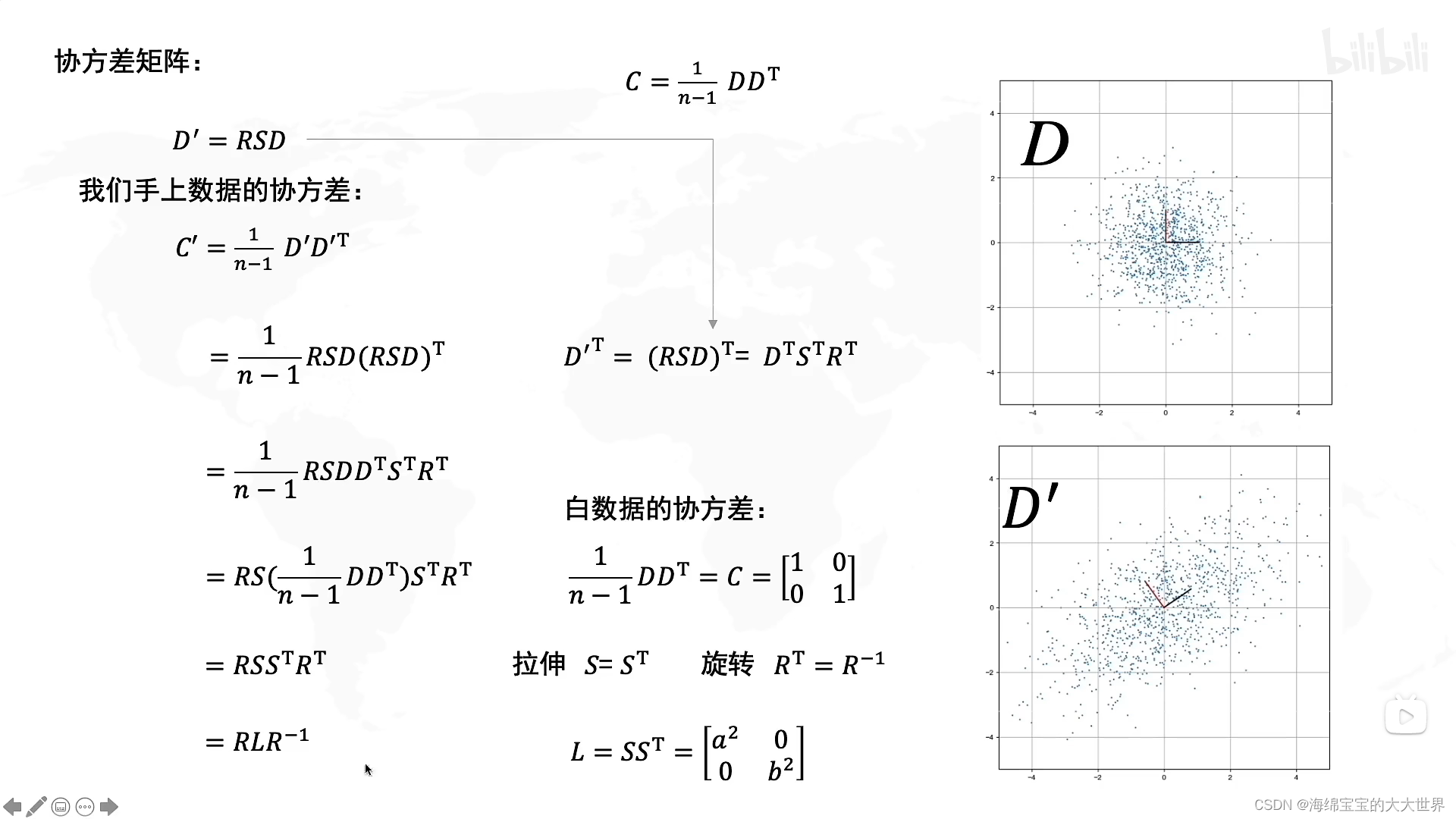
-
其中D’是我们要降维的数据,D是白数据。

- 特征向量v1和v2组成了一个R矩阵,特征值λ1和λ2组成了L矩阵
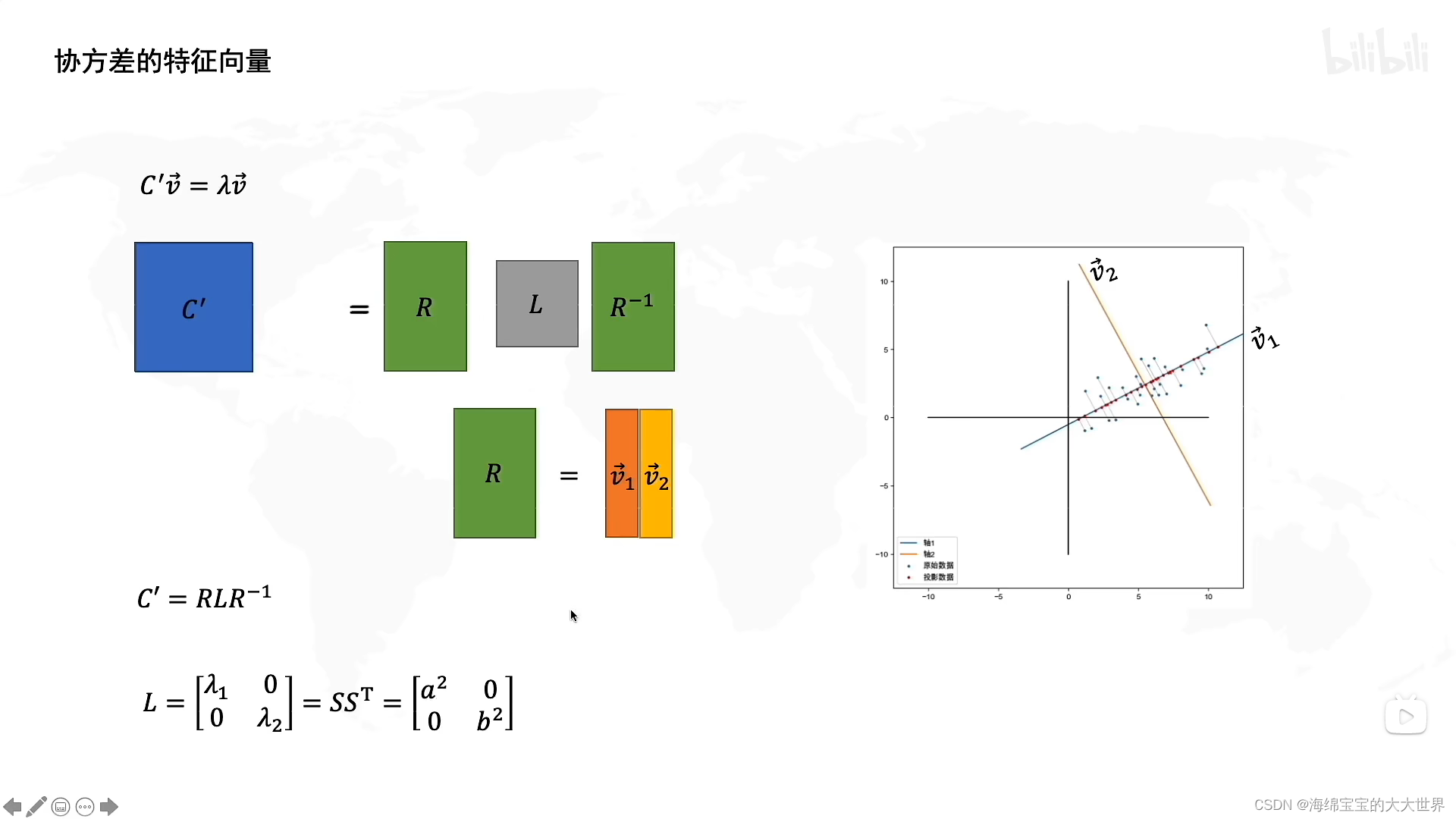
R将特征向量v1,v2组合起来,R就是坐标系旋转角度,v1是主成分一的方向,v2是主成分二的方向。
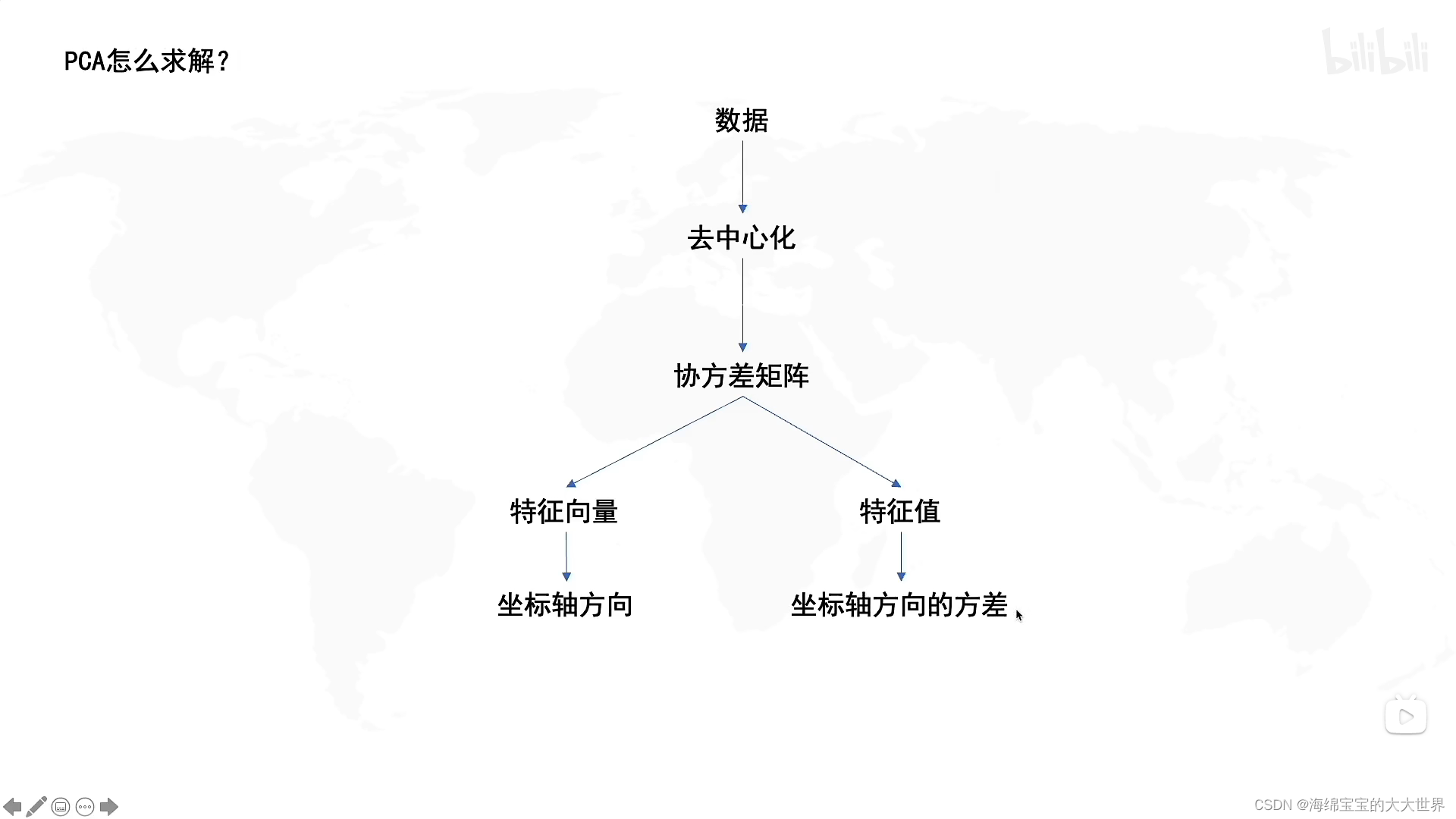
- 求解PCA总结:
1.将需要处理的数据中心点放在原点
2.求出协方差矩阵
3.使用协方差矩阵求特征向量和特征值。其中特征向量是R,旋转的方向,也就是坐标轴的方向,特征值是坐标轴方向上数据的方差。
4.得出的特征值就是各个属性的方差和,例如属性A特征值为10,B为60,C为30,那么B和C就可以表达三维的数据,方差占比为60%和30%。
代码步骤

为什么要标准化?
控制各个属性那一列的标准差在一定的范围之内,因为PCA的目标是方差最大化,将原有的数据投影到某个方向,以得到最大的方差,如果不对数据进行标准化,PCA就会严重的倾向于标准化最大的属性,不会考虑其他数值较小的属性。
python代码import pandas as pd
以下代码的结果为:
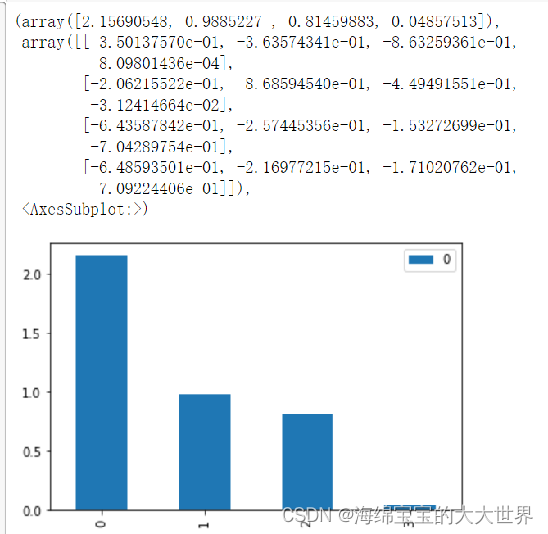
- 分别为特征值,特征向量,和各个属性的方差贡献。可以看出横坐标4的占比是最小的,在此实验中使用前三个属性来表示整体数据。特征向量的含义是:例如第一个特征向量,3.50137570e-01表示第一个属性在主成分一中的权重,-3.635743表示第二个属性在主成分一中的权重,以此类推
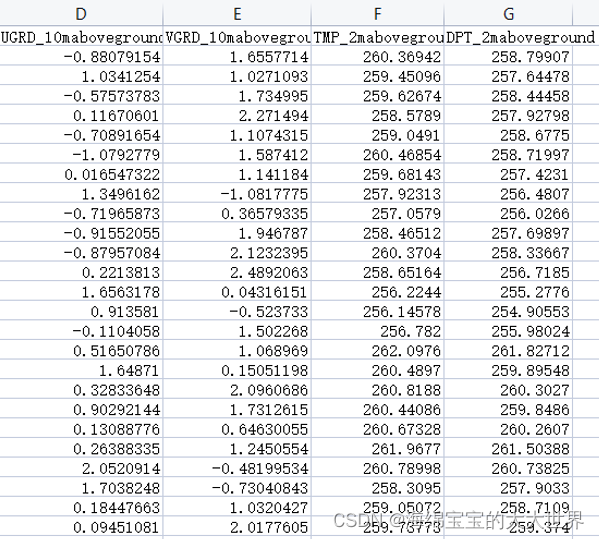

上图为初始数据4维数据,下图为得到特征向量转换回4维之后的值。有些许误差
import pandas as pd
import numpy as np
#读取数据
dt=pd.read_csv('_taiyuan_data.csv')
#将属性值拿出来
data=dt.iloc [:,3:]
data.describe()
#标准化的函数
def norm_(x):
xmean = np.mean(x,0)
std = np.std(x,0)
return (x-xmean)/std
data1 = norm_(data)
data1.describe()
#计算特征值和特征向量
vals, vecs = np.linalg.eig(np.cov(data1.T))
#将特征值从大到小排序
vals_order = np.argsort(-vals)
vals_sort = vals[vals_order]
vecs_sort = vecs[:,vals_order]
vals_sort,vecs_sort,pd.DataFrame(vals_sort).plot(kind='bar')
#如果用PCA把m个维度的数据降维成k个维度,即只用前k个主成分来表示,那么数据在主成分上的投影坐标是
#$$Y_{nk} = X_{nm}Q_{m*k}$$ $Q$为特征向量组成的矩阵
k = 3
Q = vecs_sort[:,:k]
#数据在主成分1,2,3上的投影坐标是Y,就是四维数据变成三维数据之后三维数据的坐标
#或者 Y = data1.dot(Q)
Y = np.matmul(data1,Q)
#得到去中心化的还原数据
X = np.matmul(Y,Q.T)
#X = np.matmul(Y,Q.T)*np.std(data,0)+np.mean(data,0)
D = (X[0]*data.std(0)[0]+data.mean(0)[0])
F = X[1]*data.std(0)[1]+data.mean(0)[1]
Z = X[2]*data.std(0)[2]+data.mean(0)[2]
H = X[3]*data.std(0)[3]+data.mean(0)[3]
#D.to_frame().merge(F)
D=D.to_frame().merge(F,left_index=True,right_index=True).merge(Z,left_index=True,right_index=True).merge(H,left_index=True,right_index=True)
D.to_csv('data_back')```