[Python知识库]gitmodel学习笔记（三）：利用scipy分析概率论与数理统计

引言

本篇是在复习到中途参加的一个关于gitmodel的学习活动，本系列分为三个部分，分别为高等数学、线性代数以及概率论与数理统计。本篇为第二篇——利用scipy分析概率论与数理统计，看完活动文档，查找了相关资料后，汇成笔记在这里记录一下。

scipy包介绍

感觉scipy蕴含的东西比较多，也比较杂，这里引出一些比较常用的，跟第一篇中sympy中介绍一样的表格。

scipy模块总结

这里我不会全部都介绍，主要涉及到一些我在做本次学习中感觉用得到的，以及看了资料感觉很有意思的，以上表格内容总结来源于官方文档：https://docs.scipy.org/doc/scipy/reference/ndimage.html，以下例子参考官方文档以及实验楼等资料。

常量模块

为了方便科学计算，SciPy 提供了一个叫 scipy.constants 模块，该模块下包含了常用的物理和数学常数及单位。你可以通过前面给出的链接来查看这些常数和单位，这里我们给出几个示例。

"""二进制前缀:以bytes返回指定的单位"""
print(constants.kibi)    #1024
print(constants.mebi)    #1048576
print(constants.gibi)    #1073741824
print(constants.tebi)    #1099511627776

"""时间(Time):在seconds中返回指定的单位"""
print(constants.minute)      #60.0
print(constants.hour)        #3600.0
print(constants.day)         #86400.0
print(constants.week)        #604800.0

"""长度:以meters返回指定的单位"""
print(constants.inch)              #0.0254
print(constants.foot)              #0.30479999999999996
print(constants.yard)              #0.9143999999999999
print(constants.mile)              #1609.3439999999998

线性代数模块

线性代数应该是科学计算中最常涉及到的计算方法之一，SciPy 中提供的详细而全面的线性代数计算函数，基本都在scipy.linalg里，又大致分为：基本求解方法，特征值问题，矩阵分解，矩阵函数，矩阵方程求解，特殊矩阵构造等几个小类，大部分都跟numpy类似。这里介绍一个求解函数的例子：

奇异值分解应该是每个人学习线性代数过程中的痛点，使用 SciPy 提供的 scipy.linalg.svd 函数可以十分方便地完成这个过程。例如，我们对一个 $5\times 4$ 的随机矩阵完成奇异值分解。

U, s, Vh = linalg.svd(np.random.randn(5, 4))
U, s, Vh

(array([[-0.69360296, -0.02079525, -0.25423585,  0.66155259,  0.12725879],
        [-0.02801888, -0.00145011,  0.24615542, -0.11976128,  0.96139356],
        [-0.58635567, -0.15329144,  0.6954172 , -0.30738265, -0.23366556],
        [-0.28646697,  0.86682735, -0.2056862 , -0.35247308,  0.00171486],
        [-0.30373275, -0.47400162, -0.59064351, -0.57383277,  0.0701789 ]]),
 array([2.86658847, 1.98083662, 1.55049197, 0.82843472]),
 array([[-0.80315056,  0.58402879, -0.1170798 , -0.01232335],
        [-0.55138341, -0.67654343,  0.37468133,  0.31285656],
        [ 0.14952557,  0.17570854, -0.24826402,  0.94081539],
        [ 0.16901956,  0.41270555,  0.88559088,  0.12975098]]))

最终返回酉矩阵 U 和 Vh，以及奇异值 s。

除此之外，scipy.linalg还包含像最小二乘法求解函数 scipy.linalg.lstsq。现在尝试用其完成一个最小二乘求解过程。

首先，我们给出样本的 $x$ 和 $y$ 值。然后假设其符合 $y=a{x}^2+b$ 分布。

x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

接下来，我们完成 $x^2$ 计算，并添加截距项系数 1。然后使用 linalg.lstsq 执行最小二乘法计算，返回的第一组参数即为拟合系数。

M = x[:, np.newaxis]**[0, 2]
p = linalg.lstsq(M, y)[0]
"""
array([0.20925829, 0.12013861])
"""

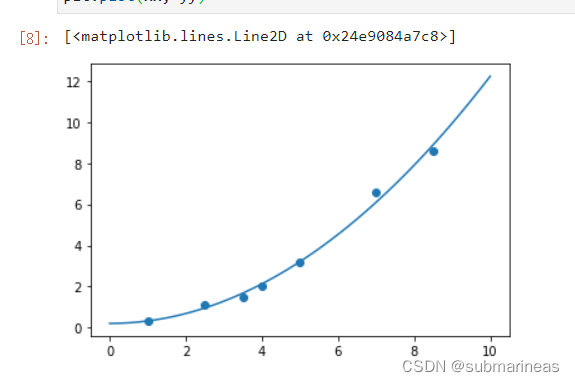
我们可以通过绘图来查看最小二乘法得到的参数是否合理，绘制出样本和拟合曲线图。

from matplotlib import pyplot as plt
%matplotlib inline

plt.scatter(x, y)
xx = np.linspace(0, 10, 100)
yy = p[0] + p[1]*xx**2
plt.plot(xx, yy)

插值函数

插值，是数值分析领域中通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。SciPy 提供的scipy.interpolate模块下方就包含了大量的数学插值方法，涵盖非常全面。下面举个简单例子：

"""随意给出一组值"""
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
plt.scatter(x, y)

"""对上述值进行线性插值"""
xx = np.array([0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5])  # 两点之间的点的 x 坐标
f = interpolate.interp1d(x, y)  # 使用原样本点建立插值函数
yy = f(xx)  # 映射到新样本点

plt.scatter(x, y)
plt.scatter(xx, yy, marker='*')

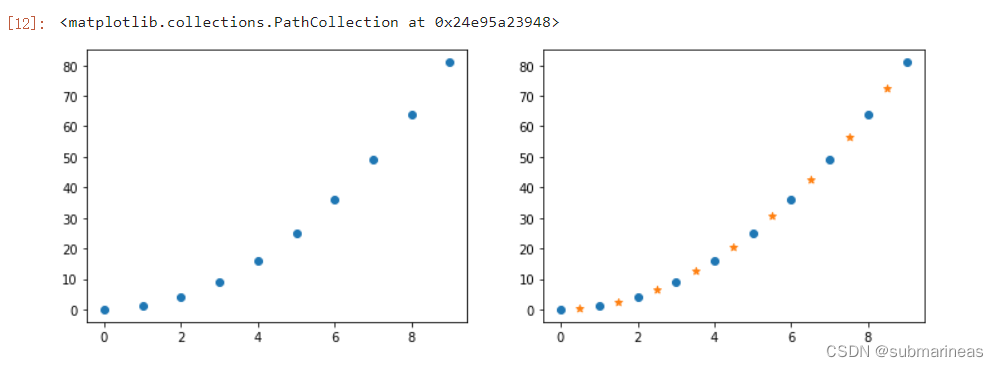
可以看到，右边图的星号点是我们插值的点，而圆点是原样本点，插值的点能准确符合已知离散数据点的趋势。

优化模块

最优化，是应用数学的一个分支，一般我们需要最小化（或者最大化）一个目标函数，而找到的可行解也被称为最优解，可能会用到最小二乘法，梯度下降法，牛顿法等最优化方法来完成。

SciPy 提供的 scipy.optimize 模块下包含大量写好的最优化方法。例如上面我们用过的 scipy.linalg.lstsq 最小二乘法函数在 scipy.optimize 模块下也有一个很相似的函数 scipy.optimize.least_squares。这个函数可以解决非线性的最小二乘法问题。

scipy.optimize 模块下最常用的函数莫过于 scipy.optimize.minimize，这个函数在第一篇sympy中对其参数进行了部分讲解，这里就不再论述。接下来，我们沿用上面 scipy.linalg.lstsq 演示时同样的数据，使用 scipy.linalg.lstsq 最小二乘法来搞定最小二乘法计算过程。这里会比上面麻烦一些，首先定义拟合函数 func 和残差函数 err_func，实际上我们需要求解残差函数的最小值。

def func(p, x):
    w0, w1 = p
    f = w0 + w1*x*x
    return f


def err_func(p, x, y):
    ret = func(p, x) - y
    return ret

p_init = np.random.randn(2)  # 生成 2 个随机数
x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])
# 使用 Scipy 提供的最小二乘法函数得到最佳拟合参数
parameters = leastsq(err_func, p_init, args=(x, y))
parameters[0]
"""
array([0.20925827, 0.12013861])
"""

不出意外的话，这里得到的结果和上面 scipy.linalg.lstsq 得到的结果一模一样。另外关于优化函数，这里提一下optimize的api：

• 多变量局部优化器包括 minimize、fmin、fmin_powell、fmin_cg、fmin_bfgs 和 fmin_ncg。

• 有限制的多变量局部优化器包括 fmin_l_bfgs_b、fmin_tnc、fmin_cobyla。

详情参照官方文档。

图像处理模块

有趣的是，SciPy 集成了大量针对图像处理的函数和方法。当然，一张彩色图片是由 RGB 通道组成，而这实际上就是一个多维数组。所以，SciPy 针对图像的处理的模块 scipy.ndimage，实际上也是针对多维数组的处理过程，你可以完成卷积、滤波，转换等一系列操作。

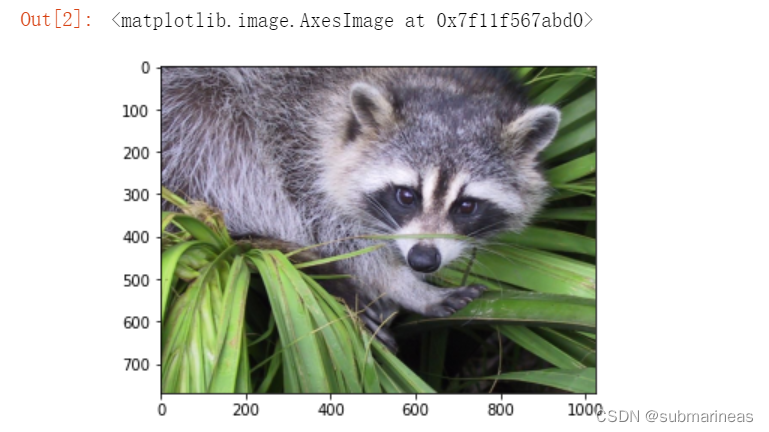
在正式了解 scipy.ndimage 模块之前，我们先使用 scipy.misc 模块中的 face 方法导入一张浣熊的示例图片。scipy.misc 是一个杂项模块，包含了一些无法被准确归类的方法。face 默认是图片的 RGB 数组，我们可以对其进行可视化还原。

from scipy import misc

face = misc.face()
plt.imshow(face)

接下来，我们尝试 scipy.ndimage 中的一些图像处理方法。例如，对图片进行高斯模糊处理。以及针对图像进行旋转变换。

from scipy import ndimage

plt.imshow(ndimage.gaussian_filter(face, sigma=5))
plt.imshow(ndimage.rotate(face, 45))

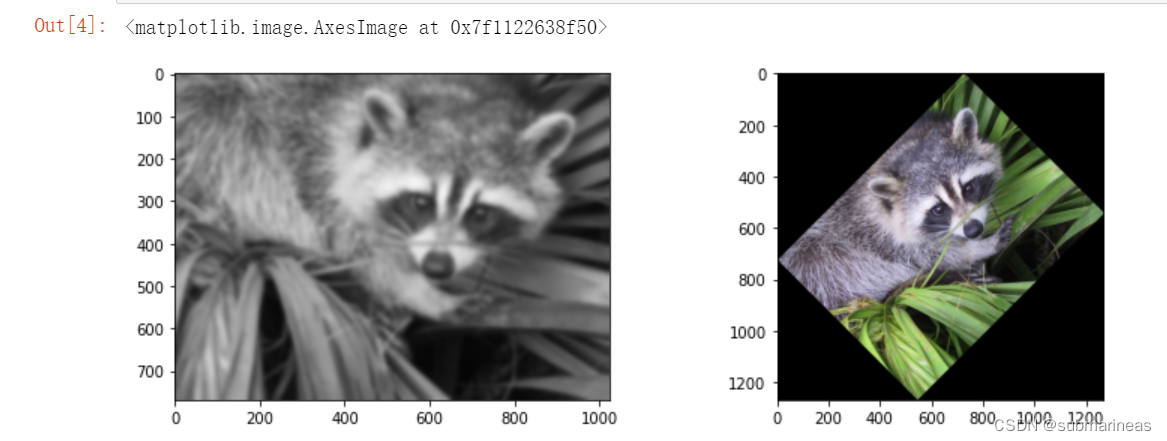
亦或者可以对图像进行卷积操作，然后再plt出来，这里就不再演示了。更多操作可以看官方文档。

统计函数模块

scipy.stats 模块包含大量概率分布函数，主要有连续分布、离散分布以及多变量分布。除此之外还有摘要统计、频率统计、转换和测试等多个小分类。基本涵盖了统计应用的方方面面。

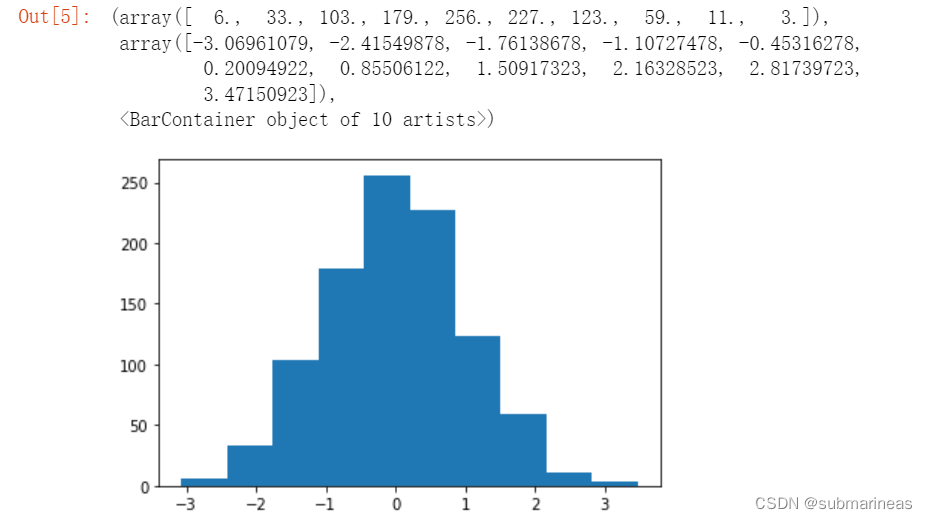
下面，我们以比较有代表性的 scipy.stats.norm 正态分布连续随机变量函数为代表进行介绍。我们尝试使用 .rvs 方法随机抽取 1000 个正态分布样本，并绘制出条形图。

from scipy.stats import norm

plt.hist(norm.rvs(size=1000))
"""
(array([  6.,  33., 103., 179., 256., 227., 123.,  59.,  11.,   3.]),
 array([-3.06961079, -2.41549878, -1.76138678, -1.10727478, -0.45316278,
         0.20094922,  0.85506122,  1.50917323,  2.16328523,  2.81739723,
         3.47150923]),
 <BarContainer object of 10 artists>)
"""

以及可以基于概率密度函数绘制出正态分布曲线，并返回数据的摘要。官方文档还有一些更加复杂的密度函数例子， 以及多种统计函数，比如线性回归。api为scipy.stats.linregress：

from scipy.stats import linregress

x = np.random.randn(200)
y = 2 * x + 0.1 * np.random.randn(200)
gradient, intercept, r_value, p_value, std_err = linregress(x, y)
gradient, intercept
"""
(2.0069839904843416, 0.0035888594932187295)
"""

积分模块

这里想重点讲一下积分模块，因为其它的比如 稀疏矩阵，MATLAB数据输入/输出 等模块短时间内我应该用不到了，而积分因为最近在复习，所以想着重描述一些相关api。

一般积分 ( quad)

首先，我们来看一个简单的例子：
$$I(a,b)={\int }_0^{1}a{x}^2+bdx$$

这里因为有两个参数，所以后续需要给a,b代数进行计算，那么代码为：

from scipy.integrate import quad

def integrand(x, a, b):
    return a*x**2 + b

a,b = 2,1
I = quad(integrand, 0, 1, args=(a,b))
I
"""
(1.6666666666666667, 1.8503717077085944e-14)
"""

quad 的第一个参数是一个“可调用”的 Python 对象（即，一个函数、方法或类实例）。请注意在这种情况下使用 lambda 函数作为参数。接下来的两个论点是积分的极限。返回值是一个元组，第一个元素保存积分的估计值，第二个元素保存误差的上限。而使用quad接口的也叫做 一般积分。

quad通过使用也允许无穷大输入 ± inf作为上下限之一。例如，假设指数积分的数值：
$$E_n(x)={\int }_1^{\infty }\frac{e^{?xt}}{t^n}dt$$

这题就需要定义，该函数的功能 special.expn可以通过 vec_expint基于例程定义一个新函数来复制quad：

from scipy.integrate import quad
def integrand(t, n, x):
    return np.exp(-x*t) / t**n
    
def expint(n, x):
    return quad(integrand, 1, np.inf, args=(n, x))[0]

vec_expint = np.vectorize(expint)  # vectorize只是序列化了expint函数方法，为了便于下面调用，但其实效率很低，我这里是参考demo，所以也就没改了，也为了与下面的做对比。
vec_expint(3, np.arange(1.0, 4.0, 0.5))
"""
array([ 0.1097,  0.0567,  0.0301,  0.0163,  0.0089,  0.0049])
"""

被积分的函数甚至可以使用 quad 参数（尽管由于使用被积函数中可能出现的数值误差，误差界可能会低估误差quad）。这种情况下的积分是
$$I_n={\int }_0^{\infty }{\int }_1^{\infty }\frac{e^{?xt}}{t^n}dtdx=\frac{1}{n}$$

result = quad(lambda x: expint(3, x), 0, np.inf)
print(result)
"""
(0.33333333324560266, 2.8548934485373678e-09)
"""

一般多重积分 ( dblquad, tplquad, nquad)
双重和三重整合的机制已被包含在函数dblquad和tplquad. 这些函数分别采用积分函数和四个或六个参数。所有内积分的极限都需要定义为函数。
$$I={\int }_{y=0}^{1/2}{\int }_{x=0}^{1?2y}xydxdy=\frac{1}{96}$$

代码为：

"""法一：使用dblquad进行二重积分"""
from scipy.integrate import dblquad
area = dblquad(lambda x, y: x*y, 0, 0.5, lambda x: 0, lambda x: 1-2*x)
area
"""
(0.010416666666666668, 1.1564823173178715e-16)
"""

"""法二："""
from scipy import integrate
def f(x, y):
    return x*y

def bounds_y():
    return [0, 0.5]

def bounds_x(y):
    return [0, 1-2*y]

integrate.nquad(f, [bounds_x, bounds_y])
"""
(0.010416666666666668, 4.101620128472366e-16)
"""

对于 n 折积分，scipy 提供了函数nquad. 积分边界是一个可迭代的对象：要么是常数边界列表，要么是非常数积分边界的函数列表。积分的顺序（以及界限）是从最里面的积分到最外面的积分。

$$I_n={\int }_0^{\infty }{\int }_1^{\infty }\frac{e^{?xt}}{t^n}dtdx=\frac{1}{n}$$

代码为：

from scipy import integrate
N = 5
def f(t, x):
   return np.exp(-x*t) / t**N

integrate.nquad(f, [[1, np.inf],[0, np.inf]])
"""
(0.20000000000002294, 1.2239614263187945e-08)
"""

gitmodel笔记

概率函数分布表示

当己知连续型随机变量的分布函数时，对其求导就可得到密度函数。分布函数是概率统计中重要的函数，正是通过它可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律,并且决定随机变量的一切其他概率特征。

1.柯西分布

柯西分布的分布函数为：$F(x)=\frac{1}{\pi }\left(\arctan x+\frac{\pi }{2}\right),?\infty <x<\infty$，求柯西分布的密度函数？
解：
$$F^{{}^{\prime }}(x)=p(x)=\frac{1}{\pi }\frac{1}{1+x^2},?\infty <x<\infty$$

所以两个代码为：

## 已知柯西分布的密度函数求分布函数
from sympy import *
x = symbols('x')
p_x = 1/pi*(1/(1+x**2))
integrate(p_x, (x, -oo, x))

## 已知柯西分布的分布函数求密度函数
f_x = 1/pi*(atan(x)+pi/2)
diff(f_x,x,1)

2.指数分布

若随机变量 $X$ 的密度函数为
$$p(x)=\{\begin{array}{rl}\lambda e^{?\lambda x},& x?0\\ 0,& x<0\end{array}$$

则称 $X$ 服从指数分布, 记作 $X～\mathrm{Exp}(\lambda )$, 其中参数 $\lambda >0$。其中 $\lambda$ 是根据实际背景而定的正参数。假如某连续随机变量 $X～\mathrm{Exp}(\lambda )$, 则表示 $X$ 仅可能取非负实数。

指数分布的分布函数为：
$$F(x)=\{\begin{array}{ll}1?{\mathrm{e}}^{?\lambda x},& x?0\\ 0,& x<0\end{array}$$

实际中不少产品首次发生故障(需要维修)的时间服从指数分布。譬如,某种热水器首次发生故障的时间 $T$ (单位:小时)服从指数分布 $\mathrm{Exp}(0.002)$, 即 $T$ 的密度函数为
$$p(t)=\{\begin{array}{cl}0.002e^{?0.002t},& t?0\\ 0,& t<0\end{array}$$

指数分布代码为：

# 指数分布
lam = float(1.5)

x = np.linspace(0,15,100)
y = lam * np.e**(-lam * x)

plt.plot(x,y,"b",linewidth=2) 
plt.xlim(-5,10)
plt.xlabel('X')
plt.ylabel('p (x)')
plt.title('exponential distribution')
plt.show()

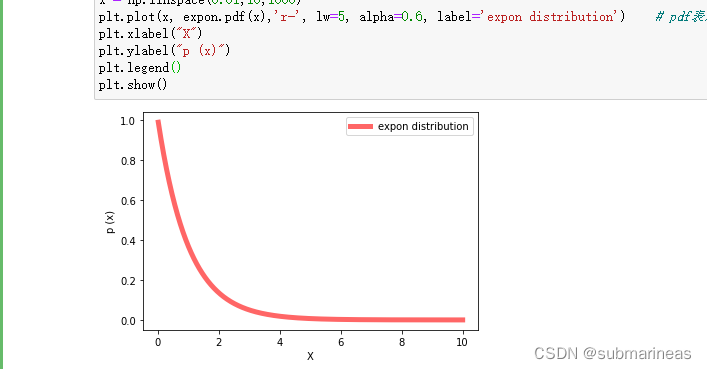
这里就不再展示图形了，可以自己运行查看。这里展示一下使用scipy画指数分布图：

# 使用scipy计算pdf画图(非自定义函数)
from scipy.stats import expon # 指数分布
x = np.linspace(0.01,10,1000)  
plt.plot(x, expon.pdf(x),'r-', lw=5, alpha=0.6, label='expon distribution')    # pdf表示求密度函数值
plt.xlabel("X")
plt.ylabel("p (x)")
plt.legend()
plt.show()

3.二项分布

用 $B_{n,k}$ 表示事件“ $n$ 重伯努里试验中成功出现 $k$ 次”。如今我们用随机变量来表示这个事件。设 $X$ 为 $n$ 重伯努里试验中成功的次数,则有 $B_{n,k}=$ “$ X=k $” 。其中 $X$ 可能取的值为 $0,1,?,n$, 它取这些值的概率为
$$P(X=x)=\left(\begin{array}{l}n\\ x\end{array}\right)p^x(1?p{)}^{n?x},x=0,1,?,n$$

例子：某特效药的临床有效率为 $0.95$， 今有 10 人服用， 问至少有 8 人治愈的概率是多少？

解：解 设 $X$ 为 10 人中被治愈的人数， 则 $X～b(10,0.95)$， 而所求概率为
$$\begin{array}{rl}P(X?8)& =P(X=8)+P(X=9)+P(X=10)\\ & =\left(\begin{array}{c}10\\ 8\end{array}\right)0.95^{8}0.05^2+\left(\begin{array}{c}10\\ 9\end{array}\right)0.95^{9}0.05+\left(\begin{array}{c}10\\ 10\end{array}\right)0.95^{10}\\ & =0.0746+0.3151+0.5987=0.9884.\end{array}$$

10 人中至少有 8 人被治愈的概率为 $0.9884$。

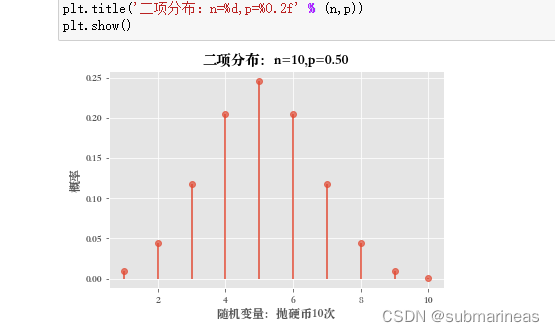
以上例子，我们也可以以抛硬币十次，用scipy.stats.binom进行画图：

# 使用scipy的pmf和cdf画图
from scipy.stats import binom
n=10
p = 0.5
x=np.arange(1,n+1,1)
pList=binom.pmf(x,n,p)
plt.plot(x,pList,marker='o',alpha=0.7,linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明：vline(x坐标值, y坐标最小值, y坐标值最大值)
'''
plt.vlines(x, 0, pList)
plt.xlabel('随机变量：抛硬币10次')
plt.ylabel('概率')
plt.title('二项分布：n=%d,p=%0.2f' % (n,p))
plt.show()

至于其它的柏松分布，正态分布以及均值分布等，因为篇幅以及参考资料，这里就不再提了，因为主题主要是用scipy来解概率论相关，如果要详述其推导以及期望与方差等，那感觉写得太长，而且根据复习节奏，更乐意去画思维导图，而不是在这里画柱状图、折线图等，所以，参考常见分布的数学期望和方差一文的表格：

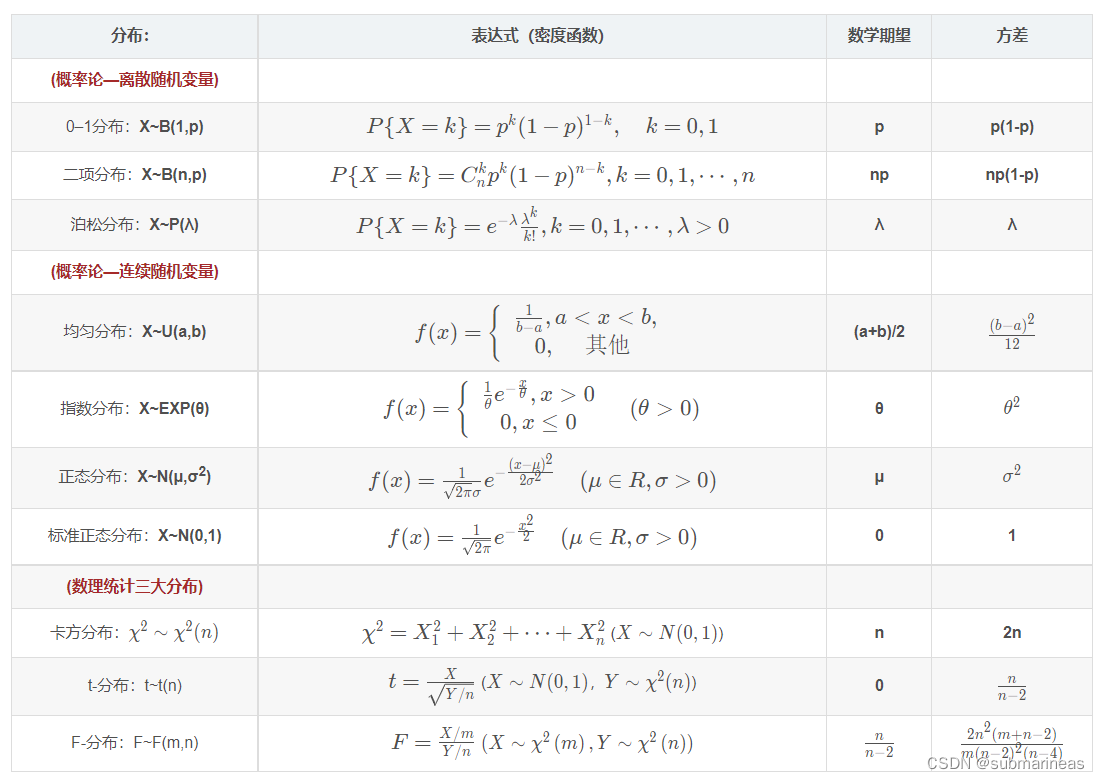
我们可以看到各种密度分布函数以及相应的期望与方差，那么与之相对应测试的scipy代码为：

# 使用scipy计算常见分布的均值与方差：(如果忘记公式的话直接查，不需要查书了)
from scipy.stats import bernoulli   # 0-1分布
from scipy.stats import binom   # 二项分布
from scipy.stats import poisson  # 泊松分布
from scipy.stats import rv_discrete # 自定义离散随机变量
from scipy.stats import uniform # 均匀分布
from scipy.stats import expon # 指数分布
from scipy.stats import norm # 正态分布
from scipy.stats import rv_continuous  # 自定义连续随机变量

print("0-1分布的数字特征：均值:{}；方差:{}；标准差:{}".format(bernoulli(p=0.5).mean(), 
                                  bernoulli(p=0.5).var(), 
                                  bernoulli(p=0.5).std()))
print("二项分布b(100,0.5)的数字特征：均值:{}；方差:{}；标准差:{}".format(binom(n=100,p=0.5).mean(), 
                                  binom(n=100,p=0.5).var(), 
                                  binom(n=100,p=0.5).std()))
## 模拟抛骰子的特定分布
xk = np.arange(6)+1
pk = np.array([1.0/6]*6)
print("泊松分布P(0.6)的数字特征：均值:{}；方差:{}；标准差:{}".format(poisson(0.6).mean(), 
                                  poisson(0.6).var(), 
                                  poisson(0.6).std()))
print("特定离散随机变量的数字特征：均值:{}；方差:{}；标准差:{}".format(rv_discrete(name='dice', values=(xk, pk)).mean(), 
                                  rv_discrete(name='dice', values=(xk, pk)).var(), 
                                  rv_discrete(name='dice', values=(xk, pk)).std()))
print("均匀分布U(1,1+5)的数字特征：均值:{}；方差:{}；标准差:{}".format(uniform(loc=1,scale=5).mean(), 
                                  uniform(loc=1,scale=5).var(), 
                                  uniform(loc=1,scale=5).std()))
print("正态分布N(0,0.0001)的数字特征：均值:{}；方差:{}；标准差:{}".format(norm(loc=0,scale=0.01).mean(), 
                                  norm(loc=0,scale=0.01).var(), 
                                  norm(loc=0,scale=0.01).std()))

lmd = 5.0  # 指数分布的lambda = 5.0
print("指数分布Exp(5)的数字特征：均值:{}；方差:{}；标准差:{}".format(expon(scale=1.0/lmd).mean(), 
                                  expon(scale=1.0/lmd).var(), 
                                  expon(scale=1.0/lmd).std()))

## 自定义标准正态分布
class gaussian_gen(rv_continuous):
    def _pdf(self, x): # tongguo 
        return np.exp(-x**2 / 2.) / np.sqrt(2.0 * np.pi)
gaussian = gaussian_gen(name='gaussian')
print("标准正态分布的数字特征：均值:{}；方差:{}；标准差:{}".format(gaussian().mean(), 
                                  gaussian().var(), 
                                  gaussian().std()))

## 自定义指数分布
import math
class Exp_gen(rv_continuous):
    def _pdf(self, x,lmd):
        y=0
        if x>0:
            y = lmd * math.e**(-lmd*x)
        return y
Exp = Exp_gen(name='Exp(5.0)')
print("Exp(5.0)分布的数字特征：均值:{}；方差:{}；标准差:{}".format(Exp(5.0).mean(), 
                                  Exp(5.0).var(), 
                                  Exp(5.0).std()))

## 通过分布函数自定义分布
class Distance_circle(rv_continuous):                 #自定义分布xdist
    """
    向半径为r的圆内投掷一点，点到圆心距离的随机变量X的分布函数为:
    if x<0: F(x) = 0;
    if 0<=x<=r: F(x) = x^2 / r^2
    if x>r: F(x)=1
    """
    def _cdf(self, x, r):                   #累积分布函数定义随机变量
        f=np.zeros(x.size)                  #函数值初始化为0
        index=np.where((x>=0)&(x<=r))           #0<=x<=r
        f[index]=((x[index])/r[index])**2       #0<=x<=r
        index=np.where(x>r)                     #x>r
        f[index]=1                              #x>r
        return f
dist = Distance_circle(name="distance_circle")
print("dist分布的数字特征：均值:{}；方差:{}；标准差:{}".format(dist(5.0).mean(), 
                                  dist(5.0).var(), 
                                  dist(5.0).std()))

"""
0-1分布的数字特征：均值:0.5；方差:0.25；标准差:0.5
二项分布b(100,0.5)的数字特征：均值:50.0；方差:25.0；标准差:5.0
泊松分布P(0.6)的数字特征：均值:0.6；方差:0.6；标准差:0.7745966692414834
特定离散随机变量的数字特征：均值:3.5；方差:2.916666666666666；标准差:1.707825127659933
均匀分布U(1,1+5)的数字特征：均值:3.5；方差:2.083333333333333；标准差:1.4433756729740643
正态分布N(0,0.0001)的数字特征：均值:0.0；方差:0.0001；标准差:0.01
指数分布Exp(5)的数字特征：均值:0.2；方差:0.04000000000000001；标准差:0.2
标准正态分布的数字特征：均值:-6.963277549967673e-16；方差:0.9999999993070242；标准差:0.999999999653512
Exp(5.0)分布的数字特征：均值:0.20826187507584426；方差:0.03678414422845682；标准差:0.19179192951857182
dist分布的数字特征：均值:3.333333333333333；方差:1.388888888888891；标准差:1.1785113019775801
"""

大数定理

大数定律主要有两种表达方式，分别为：

• 伯努利大数定律：
  
  设 $S_n$ 为 $n$ 重伯努利试验（结果只有0-1）中事件 $A$ 发生的次数，$\frac{S_n}{n}$就是事件 $A$ 发生的频率， $p$ 为每次试验中 $A$ 出现的概率， 则对任意的 $\epsilon >0$， 有
  $$\underset{n\to \infty }{\lim }P\left(\left|\frac{S_n}{n}?p\right|<\epsilon \right)=1$$
• 辛钦大数定律：
  
  设 { X n } \left\{X_{n}\right\} {Xn?} 为一独立同分布的随机变量序列， 若 $X_i$ 的数学期望存在， 则 { X n } \left\{X_{n}\right\} {Xn?} 服从大数定律， 即对任意的 $\epsilon >0$，${\lim }_{n\to \infty }P\left(\left|\frac{1}{n}{\sum }_{i=1}^n{X}_i?\frac{1}{n}{\sum }_{i=1}^{n}E\left(X_i\right)\right|<\epsilon \right)=1$成立。
  
  对于独立同分布且具有相同均值 $\mu$ 的随机变量X，$X_1,X_2,\dots \dots X_n$ ，当 $n$ 很大时，它们的算术平均数 $\frac{1}{n}{\sum }_{i=1}^n{X}_i$ 很接近于 $\mu$。也就是说可以使用样本的均值去估计总体均值.

关于前者，伯努利大数定律可以使用蒙特卡洛模拟进行求值，即对于任意函数，选择在【0,1】上的积分，这里选择$y=x^2$：

# 使用蒙特卡洛法计算y=x^2在【0，1】上的定积分
from scipy.stats import uniform
def MonteCarloRandom(n):
    x_n = uniform.rvs(size = n)  # 随机选择n个x随机数
    y_n = uniform.rvs(size = n)  # 随机选择n个y随机数
    f_x = np.square(x_n)    # 函数值f_x = x**2
    binory_y = [1.0 if y_n[i] < f_x[i] else 0 for i in range(n)]    # 如果y<x**2则为1，否则为0
    J = np.sum(binory_y) / n
    return J
    
print("y=x**2在[0,1]的定积分为：",integrate(x**2, (x,0,1)))
print("模拟10次的定积分为：",MonteCarloRandom(10))
print("模拟100次的定积分为：",MonteCarloRandom(100))
print("模拟1000次的定积分为：",MonteCarloRandom(1000))
print("模拟10000次的定积分为：",MonteCarloRandom(10000))
print("模拟100000次的定积分为：",MonteCarloRandom(100000))
print("模拟1000000次的定积分为：",MonteCarloRandom(1000000))

"""
y=x**2在[0,1]的定积分为： 1/3
模拟10次的定积分为： 0.3
模拟100次的定积分为： 0.3
模拟1000次的定积分为： 0.34
模拟10000次的定积分为： 0.3302
模拟100000次的定积分为： 0.33285
模拟1000000次的定积分为： 0.333851
"""

中心极限定理

中心极限定理是概率论中讨论随机变量序列部分和的分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础，研究由许多独立随机变量组成和的极限分布律。指出了大量随机变量近似服从正态分布的条件。

大数定律讨论的是在什么条件下（独立同分布且数学期望存在），随机变量序列的算术平均依概率收敛到其均值的算术平均。下面，我们来讨论下什么情况下，独立随机变量的和$Y_n={\sum }_{i=1}^n{X}_i$的分布函数会依分布收敛于正态分布。我们使用一个小例子来说明什么是中心极限定理：

我们想研究一个复杂工艺产生的产品误差的分布情况，诞生该产品的工艺中，有许多方面都能产生误差，如：每个流程中所需的生产设备的精度误差、材料实际成分与理论成分的差异带来的误差、工人当天的专注程度、测量误差等等。由于这些因素非常多，每个影响产品误差的因素对误差的影响都十分微笑，而且这些因素的出现也十分随机，数值有正有负。现在假设每一种因素都假设为一个随机变量$X_i$，先按照直觉假设$X_i$服从$N(0,{\sigma }_i^2)$，零均值假设是十分合理的，因为这些因素的数值有正有负，假设每一个因素的随机变量的方差${\sigma }_i^2$是随机的。接下来，我们希望研究的是产品的误差$Y_n=X_1+X_2+?+X_n$，当n很大时是什么分布？

# 模拟n个正态分布的和的分布
from scipy.stats import norm
def Random_Sum_F(n):
    sample_nums = 10000
    random_arr = np.zeros(sample_nums)
    for i in range(n):
        mu = 0
        sigma2 = np.random.rand()
        err_arr = norm.rvs(size=sample_nums)
        random_arr += err_arr
    plt.hist(random_arr)
    plt.title("n = "+str(n))
    plt.xlabel("x")
    plt.ylabel("p (x)")
    plt.show()

Random_Sum_F(2)
Random_Sum_F(10)
Random_Sum_F(100)
Random_Sum_F(1000)
Random_Sum_F(10000)

这里的图就不再展示，如果正态分布实验没发现规律，还可以去尝试泊松分布、指数分布等，那最终实验说明了一个道理：假设 { X n } \left\{X_{n}\right\} {Xn?} 独立同分布、方差存在， 不管原来的分布是什么， 只要 $n$ 充分大，就可以用正态分布去逼近随机变量和的分布，所以这个定理有着广泛的应用。下面，我们来看看如何使用中心极限定理产生一组正态分布的随机数！

计算机往往只能产生一组傅聪均匀分布的随机数，那么如果我们想要产生一组服从正态分布$N(\mu ,{\sigma }^2)$的随机数，应该如何操作呢？设随机变量 $X$ 服从 $(0,1)$ 上的均匀分布， 则其数学期望与方差分别为 $1/2$ 和 $1/12$。 由此得 12 个相互独立的 $(0,1)$ 上均匀分布随机变量和的数学期望与方差分别为 6 和 1。因此：

• 产生 12 个 $(0,1)$ 上均匀分布的随机数, 记为 $x_1,x_2,?,x_{12}$。
• 计算 $y=x_1+x_2+?+x_{12}?6$， 则由中心极限定理知， 可将 $y$ 近似看成来自标准正态分布 $N(0,1)$ 的一个随机数。
• 计算 $z=\mu +\sigma y$， 则可将 $z$ 看成来自正态分布 $N\left(\mu ,{\sigma }^2\right)$ 的一个随机数。
• 重复N次就能获得N个服从正态分布$N\left(\mu ,{\sigma }^2\right)$ 的随机数。

三大分布

参数估计之点估计