开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> Python知识库 -> 第五单元用python学习微积分（三十四）泰勒级数 -> 正文阅读

[Python知识库]第五单元用python学习微积分（三十四）泰勒级数

本文内容来自于学习麻省理工学院公开课：单变量微积分-泰勒级数-网易公开课

Bullseye：第一单元用python学习微积分（一）安装开发环境Anaconda 和导数（上）- 1/x的导数

质心问题Center of Mass - Sciencetopia

重心问题Center of Gravity Definition, Equation and Calculation

Bullseye：第一单元用python学习微积分（二）VSCode 、PYGame 和导数（上）- 瞬时速度

2、用级数的想法来考虑这个问题,老师的思想实验

（1）设置

（2）计算

（3）计算跨越26个单位长度距离需要多少木块堆积？

（4）老师要求注意，尽管这个级数是没有极限的，但是这个级数的增长十分的缓慢。

三、幂级数

1、几何级数（Geomeric Series）

4、泰勒公式（Taylor's Formula）

5、泰勒公式的应用（求取 e ）

6、求取sin(x)

7、求取cos(x)

一、重心和质心

1、质心

（1）一个物体

刚体由大量粒子组成，刚体的质量是单个粒子质量的总和。但是，我们可以考虑物体上的一个点，使得物体的全部质量都集中在它上面，并且当施加相同的力时，该点的运动与与物体质量相同的粒子的运动相同.这个点称为质心。因此，物体的质心是施加的力产生线性加速度但没有旋转的点。

单个物体上的受力是由其上面每个粒子所受力的总和

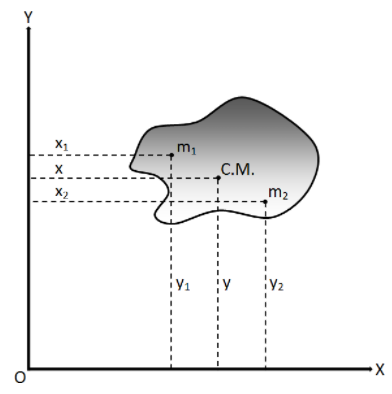
设置：如图总质量为M；质心为C.M.； 'm1, m2 ...' 为物体上某点的质量

质心公式（center of mass [x, y]）= $[ \frac{m_1x_1+m_2x_2+m_3x_3+...}{M} , \frac{m_1y_1+m_2y_2+m_3y_3+...}{M} ]$

（2）系统质心：

设置：两个质量为m1和m2的物体，如图所示。让质量通过刚性杆连接，并让C是它们的质心。

有公式： $\frac{m_1}{x_1} = \frac{m_2}{x_2}$

2、重心

重心是物体的重量作用并且物体上的总重力扭矩为零的点，简写C.G.

（1）单一物体

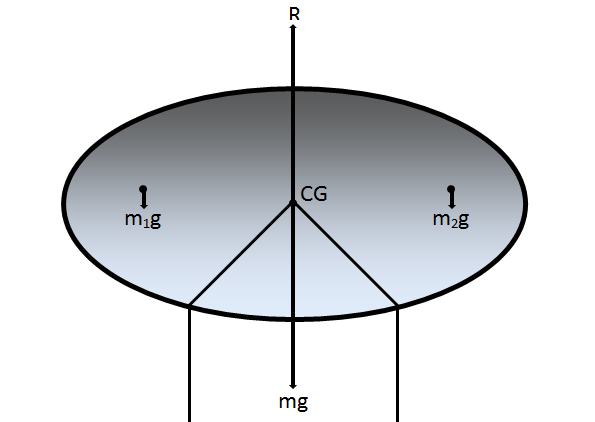
设置：物体上某粒子的重力 $m_ig$ ， $r_i$ 是这个粒子从纸板的 CG 的位置向量， $t_i$ 是这个粒子上重力的扭矩

$t_i = r_i \times m_ig$

我们知道在CG点总重力扭矩是 0，所以有

$\sum_{i=1}^{n}t_i =\sum_{i=1}^{n} r_i \times m_ig = 0$

由于 g 是常数， $\sum_{i=1}^{n} r_i \times m_i = 0$

（2）系统重心：

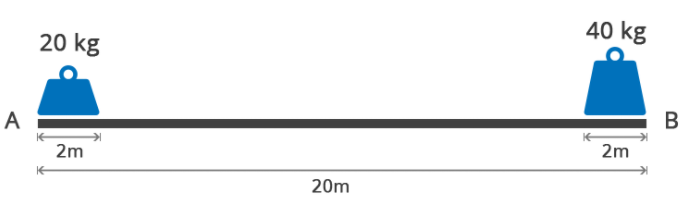
设置：两个宽2m的铁块 a, b，分别重20kg，40kg，并分别放置在木板两侧A、B，木板长20m。

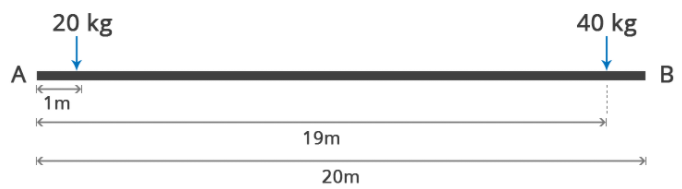
a 的重心距离 A 点1m，而 b 的重心距离A点19m

以左侧A点为基准

系统重心 = 总重力扭矩 $\div$ 总的力臂 = （A的力臂 $\times$ A点受力 + B的力臂 $\times$ B点受力） $\div$ （A点受力 + B点力臂）

总重力扭矩= $1 \times 20 + 19\times40 = 780 kg.m$

系统重心距离左侧= $\frac{780}{20+40} = 13 m$

3、不同形状的重心位置

体型	CG位置
细均匀条	条的中点
圆环	环的中心
圆盘	磁盘中心
球体、空心球体、环形盘	在它的中心
立方体或矩形块	对角线的交点
三角板	中线的交点
方形层、平行四边形和矩形层	对角线的交点
圆柱	轴的中点
圆锥或金字塔	在与底面中心顶点相接的线上，距底面的距离等于该线长度的1/4

二、重心问题

如图，有多个积木搭在一起，由下向上，每块都向左偏移一定的距离，问最上面那一块的右测可不可以偏移到最下面的积木的左测以左。

1、实验

老师用几块积木做了这个实验，并且成功了。这里的秘密就是要从上向下布置。

其原理是，由于只要在积木的重心处有支撑，积木就可以立住。

第一块积木的重心在他的中心位置，所以第二块积木要放在第一块的一半处（积木都是等大小的，所以我们只需要考虑水平方向的位置，xCenter1）。第一块和第二块积木形成了新的系统，这个系统的重心在原第一块和第二块重心的平均的位置（ $\frac{xCenter1+xCenter2}{2}$ ）, 以此类推当有n个积木以此方法布置时，它们组成的系统的重心为( $\frac{xCenter1+xCenter2+...+xCenterN}{N}$ )

模拟程序：

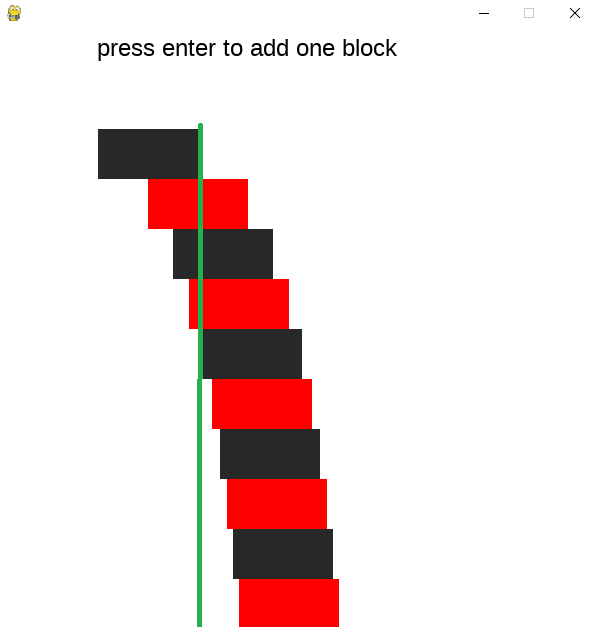
pygame基础上制作的模拟程序

链接：百度网盘请输入提取码

提取码：1g1u

解压7z，并在解压目录中运行 AddRectangles.py。程序中点击键盘回车可以添加一个积木。

2、用级数的想法来考虑这个问题,老师的思想实验

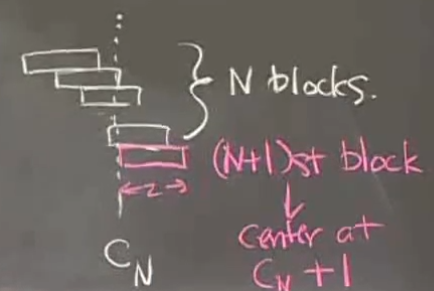
（1）设置：积木长 L = 2，重力 W = 1 ，位置因素只考虑x方向变化，使用贪婪算法，从上向下布置，第n+1块积木所在的位置是：第n块积木的重心和第n+1块积木重心的平均数，也就是 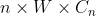$n \times W \times C_n$ ? 和 $W \times C_{n+1}$ 的平均数。由于每块积木的重量相等，则第n块积木累积了n的重量，而n+1块积木有重量 1，它们的平均值是

（2）计算

考虑重心中系统重心的公式

以原点计，

系统重心 = 总重力扭矩? $\div$ 总的力臂 = （A的力臂? $\times$ A点受力 + B的力臂? $\times$ B点受力）? $\div$ （A点受力 + B点力臂）

也就是第n+1块积木的左侧是在前n块积木的重心 $C_n$ （W=1，重力为 n ）下方，也就是说第n+1块积木的重心在 $C_n + 2/2 = Cn +1$ （重力为 1 ）

再把重量考虑进去，则这个新的重心在 $\frac{nC_n +1 (C_n+1)}{n+1} = \frac{(n+1)C_n+1}{n+1} = C_n+\frac{1}{n+1}$

程序：

import numpy as np 
from sympy import *
import matplotlib.pyplot as plt 

def GetCenter(steps, weight, length):
    Cn = 0
    for i in range(steps):
        n = i
        Cn = (Cn*weight*n + (Cn + length/2.0)*weight)/(n+1)
        print(Cn)
        
W = 1
L = 2
GetCenter(100,weight=W,length =L)

1.0
1.5
1.8333333333333333
2.083333333333333
2.2833333333333328
...
5.177377517639616
5.187377517639615

按公式展开：

$C_0 = 1$

$C_1 = 1+\frac{1}{2}$

$C_2 = 1+\frac{1}{2} + \frac{1}{3}$

....

$C_n =1+\frac{1}{2} +\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}$

由上一章得知：

Bullseye：第五单元用python学习微积分（三十三）反常积分（下）-- 无穷级数和收敛判定

黎曼上和（ $\Delta x= 1$ ） $UpperRiemanSum=1+\frac{1}{2} +...+\frac{1}{N-1} = \infty$

显然这个 $C_n \rightarrow_{n \rightarrow\infty} \infty$ （发散的）

（3）计算跨越26个单位长度距离需要多少木块堆积？

由上一章的知识可知， $ln(n)$ ? 近似并小于 $C_n$ （ $C_n<ln(n)+1$ ）,

这里要注意，每个木块被定义为2个单位距离，所以当我们需要跨越26个单位距离时，

首先要减掉最下面那块的2个单位距离，然后就是其余的积木的重心到目标位置的距离即24个单位距离，也就是 $C_n = 24$ ，由于 $ln(n) < C_n<ln(n)+1$ ，也就是让第24个单位距离处为这n块积木的重心，求 n+1（显然 n 是整数）。

x = symbols('x')
eq = ln(x)-24
eq1 = Eq(eq,0)
solveX = solve(eq1)
print(int(solveX[0]))
26489122129

$n =(int) e^{24} +1 = 26489122129+1=26489122130$

假设木块高3cm，这些木块摞起来有多高呢？ $26489122130*3/100 \approx 8 * 10^8 (m)$ ，大约等于地球到月亮的距离的2倍

（4）老师要求注意，尽管这个级数是没有极限的，但是这个级数的增长十分的缓慢。

三、幂级数

1、几何级数（Geomeric Series）

当 |x| < 1

$1+x+x^2+x^3... = \frac{1}{1-x}$

（1）证明

假设有 $1+x+x^2+x^3+... = S$

$(1+x+x^2+x^3+... )\times x = S \times x$

$x+x^2+x^3+x^4+... = S \times x$

$S - x+x^2+x^3+x^4+... =S- S \times x$

由于 $1+x+x^2+x^3+... = S$

$1= S - S \times x$

$S = \frac{1}{1-x}$

这个证明要求S首先要存在，也就是这个幂级数要是收敛的，不能是发散的。

当 $x \geq 1$ 时，等式 $1+x+x^2+x^3+... = S$ 会变成 $\infty = \infty$ ,造成结果无意义。

2、幂级数的一般形式

（1）公式

$a_0+ a_1x + a_2x^2 + a_3x^3+...$

$= \sum_{n=0}^{\infty} a_nx^n$

$|x|<R$ (收敛半径 radius of converges)

$-R < x <R$ （级数收敛点集区间）

当 $|x|>R$ ， $\sum_{n=0}^{\infty} a_nx^n$ 是发散的

当 $|x|=R$ , 是边界，并不会被使用

（2）如何判断

$|a_nx^n|\rightarrow0$ 以指数速度趋向0 ，当 $|x|<R$

$|a_nx^n|$ 不会趋向0 ，当 $|x|>R$

3、收敛幂级数的法则（和多项式类似）

$f(x) + g(x) , f(x)g(x) , f(g(x)) ,\frac{f(x)}{g(x)}, \frac{d}{dx} f(x), \int f(x)dx$ 这些运算对幂级数来说都是成立的

（1）运算举例

$\frac{d}{dx}(a_0 + a_1x+a_2x^2+a_3x^3+...)= a_1 + 2a_2x + 3a_3x^2+...$

$\int(a_0 + a_1x+a_2x^2+a_3x^3+...)dx = const + a_0x + \frac{1}{2}a_1x^2 + \frac{1}{3}a_2x^3 + \frac{1}{4}a_3x^4 +...$

4、泰勒公式（Taylor's Formula）

注意：使用泰勒公式时，当 n=0 时，约定俗成 0! = 1

泰勒公式的本质是近似，当 f(x)在 $x_0$ 处有n阶导数，则有这个函数可以用幂函数近似替代，有公式

$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(x_0)}{n!} (x-x_0)^n$

当这个函数在 x=0 处有n阶导数，泰勒公式变换为更常用的麦克劳林公式

$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n$

当这个展开式n值越大，近似度就越高

通常在幂级数中， $a_n=\frac{f^{(n)}(0)}{n!}$

证明：

$f(x) = a_0 + a_1x+a_2x^2+a_3x^3+...$

$f'(x) = a_1 + 2a_2x + 3a_3x^2+...$

$f''(x) = 2a_2 + 3 \times 2 a_3x+...$

$f'''(x) = 3\times 2a_3 + 4 \times 3\times 2 a_4+...$

x 取 0， $f'''(0) = 3\times 2a_3$

$\frac{f^{(3)}(0)}{3 \times 2\times1} =\frac{f^{(3)}(0)}{3!}= a_3$

5、泰勒公式的应用（求取 e ）

我们知道，当 $f(x) =e^x 有 f'(x) = e^x, f''(x) = e^x, f'''(x) = e^x...$ , $f^{(n)}(0) = 1$

所以我们可以把它带入泰勒公式，有

$e^x = \sum_{n=0}^{\infty} \frac{1}{n!} x^n$

而 $e^1 = 1+1 + \frac{1}{2!} + \frac{1}{3!}+...$

6、求取sin(x)

我们知道，当 $f(x) =sin(x) 有 f'(x) = cos(x), f''(x) = -sin(x), f'''(x) = -cos(x)...$

$sin(x) =\frac{sin(0)}{1} + \frac{cos(0)}{1!}x - \frac{sin(0)}{2!}x^2 - \frac{cos(0)}{3!}x^3 + \frac{sin(0)}{4!}x^4 + \frac{cos(0)}{5!}x^5 + ..$

$=x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 ...$

7、求取cos(x)

$cos(x) =\frac{cos(0)}{1} - \frac{sin(0)}{1!}x - \frac{cos(0)}{2!}x^2 + \frac{sin(0)}{3!}x^3 + \frac{cos(0)}{4!}x^4 - \frac{sin(0)}{5!}x^5 + ..$

$=1 - \frac{1}{2!} x^2 + \frac{1}{4!}x^4...$

Python知识库最新文章

Python中String模块

【Python】 14-CVS文件操作

python的panda库读写文件

使用Nordic的nrf52840实现蓝牙DFU过程

【Python学习记录】numpy数组用法整理

Python学习笔记

python字符串和列表

python如何从txt文件中解析出有效的数据

Python编程从入门到实践自学/3.1-3.2

python变量

加:2022-07-03 10:44:49 更:2022-07-03 10:45:11

360图书馆购物三丰科技阅读网日历万年历 2025年5日历

-2025/5/2 0:37:34-

图片自动播放器
↓图片自动播放器↓

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

网站联系: qq:121756557 email:121756557@qq.com IT数码

[Python知识库]第五单元 用python学习微积分（三十四）泰勒级数

一、重心和质心

1、质心

（1）一个物体

（2）系统质心：

2、重心

（1）单一物体

（2）系统重心：

3、不同形状的重心位置

二、重心问题

1、实验

2、用级数的想法来考虑这个问题,老师的思想实验

（2）计算

（3）计算跨越26个单位长度距离需要多少木块堆积？

（4）老师要求注意，尽管这个级数是没有极限的，但是这个级数的增长十分的缓慢。

三、幂级数

1、几何级数 （Geomeric Series）

（1）证明

2、幂级数的一般形式

（1）公式

（2）如何判断

3、收敛幂级数的法则（和多项式类似）

4、泰勒公式（Taylor's Formula）

5、泰勒公式的应用（ 求取 e ）

6、求取sin(x)

7、求取cos(x)

[Python知识库]第五单元用python学习微积分（三十四）泰勒级数

1、几何级数（Geomeric Series）

5、泰勒公式的应用（求取 e ）