以下资料引用至百度百科
?
康威生命游戏(Game of Life),剑桥大学约翰·何顿·康威设计的计算机程序。
概述:
生命游戏没有游戏玩家各方之间的竞争,也谈不上输赢,可以把它归类为仿真游戏。事实上,也是因为它模拟和显示的图像看起来颇似生命的出生和繁衍过程而得名为“生命游戏”。在游戏进行中,杂乱无序的细胞会逐渐演化出各种精致、有形的结构;这些结构往往有很好的对称性,而且每一代都在变化形状。一些形状一经锁定就不会逐代变化。有时,一些已经成形的结构会因为一些无序细胞的“入侵”而被破坏。但是形状和秩序经常能从杂乱中产生出来。
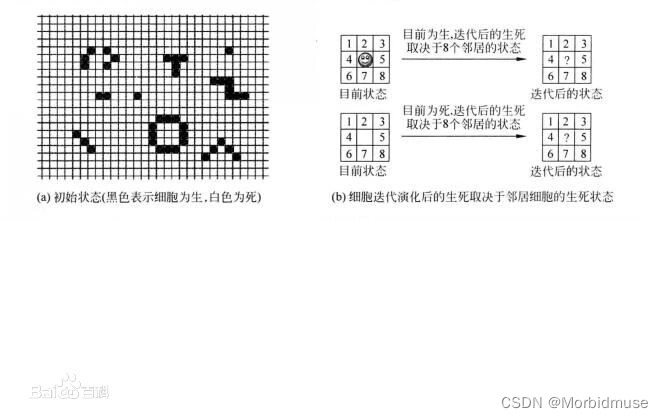
每个方格中都可放置一个生命细胞,每个生命细胞只有两种状态:
“生”或“死”。用黑色方格表示该细胞为“生”,空格(白色)表示该细胞为“死”。或者说方格网中黑色部分表示某个时候某种“生命”的分布图。生命游戏想要模拟的是:随着时间的流逝,这个分布图将如何一代一代地变化。
生存规则:
?游戏开始时,每个细胞随机地设定为“生”或“死”之一的某个状态。然后,根据某种规则,计算出下一代每个细胞的状态,画出下一代细胞的生死分布图。
应该规定什么样的迭代规则呢?需要一个简单的,但又反映生命之间既协同又竞争的生存定律。为简单起见,最基本的考虑是假设每一个细胞都遵循完全一样的生存定律;再进一步,把细胞之间的相互影响只限制在最靠近该细胞的8个邻居中。
也就是说,每个细胞迭代后的状态由该细胞及周围8个细胞状态所决定。作了这些限制后,仍然还有很多方法来规定“生存定律”的具体细节。例如,在康威的生命游戏中,规定了如下生存定律。
(1)当前细胞为死亡状态时,当周围有3个存活细胞时,则迭代后该细胞变成存活状态(模拟繁殖);若原先为生,则保持不变。
(2)当前细胞为存活状态时,当周围的邻居细胞低于两个(不包含两个)存活时,该细胞变成死亡状态(模拟生命数量稀少)。
(3)当前细胞为存活状态时,当周围有两个或3个存活细胞时,该细胞保持原样。
(4)当前细胞为存活状态时,当周围有3个以上的存活细胞时,该细胞变成死亡状态(模拟生命数量过多)。
可以把最初的细胞结构定义为种子,当所有种子细胞按以上规则处理后,可以得到第1代细胞图。按规则继续处理当前的细胞图,可以得到下一代的细胞图,周而复始。
上面的生存定律当然可以任意改动,发明出不同的“生命游戏”。
?
?图片解释:
?
最近看丹尼尔.丹尼特的《直觉泵》,书中简单介绍了两个计算机科学方面的思考工具,一个是寄存器机(一种假想的计算机,类似于图灵机),?还有康威的生命游戏。
遂利用python的turtle模块简单模拟一下
1、
根据一个二维数组arr绘制图形 当arr[i,j]==1 黑色,表示生,当arr[i,j]==0 白色,表示死。
文件draw_pic.py
# -*- coding:utf-8 -*-
# Author : MorbidMuse
# data : 2022/7/15 8:24
# 根据一个二维数组arr绘制图形 当arr[i,j]==1 黑色,表示生,当arr[i,j]==0 白色,表示死
import turtle
import numpy as np
def my_goto(t,x,y):
t.up()
t.goto(x,y)
t.down()
def draw_square(t,d,color):
t.fillcolor(color)
t.begin_fill()
t.setheading(0)
for i in range(4):
t.fd(d)
t.left(90)
t.end_fill()
def draw(arr,x0,y0,d):
'''
:param m: 二维列表行数
:param n: 二维列表列数
:param x0: 绘制起始点的x坐标
:param y0: 绘制起始点的y坐标
:param d: 绘制小正方形的边长
:return:
'''
t = turtle.Turtle()
t.pencolor('orange')
turtle.tracer(0)
my_goto(t,x0,y0)
m,n = arr.shape
for i in range(m):
for j in range(n):
if arr[i,j] == 1:
color = 'black'
else:
color = 'white'
draw_square(t,d,color)
t.fd(d)
t.backward(d*n)
if i != m-1:
t.setheading(-90)
t.fd(d)
turtle.update()
# turtle.done()
if __name__ == '__main__':
arr = np.array([[0,1,0],
[1,0,1],
[0,0,1]])
draw(arr,-300,0,30)
turtle.done()
?结果:

?2、life_game.py? ?注意这个脚本导入了上一个脚本
# -*- coding:utf-8 -*-
# Author : MorbidMuse
# data : 2022/7/15 7:56
"""
模拟生命游戏:
在一个二维平面的世界,物理规则如下:
1.整个平面被分成m行n列的二维表格
2.每个单元格只有两种状态,0代表死,用白色表示;1代表生,用黑色表示
3.每一个单元格周围有8个邻居,分别位于东南西北,以及对角线方向的东北,东南,西南,西北。
4.单元格在下一个时刻的状态取决于其当前时刻邻居的存活状态:
若邻居存活数等于3,则生;
若邻居存活数等于2,则保持当前状态;
其他情况,小于2(太孤单了),或者大于3(太拥挤了),则死
本脚本的功能:
给定一个二维数组表示世界的开端,通过turtle绘制其图形表示
迭代几代,观察生命游戏世界的变化
"""
import numpy as np
from draw_pic import draw
import turtle
def live_or_die(arr):
'''
计算下一个时刻,当前单元格的存活状态
:param arr: 3*3的二维数组,代表当前单元格和他的所有邻居
:return:
0:die
1:live
'''
crrent_status = arr[1,1]
neighbor_live_num= 0
if crrent_status == 1:
neighbor_live_num = np.count_nonzero(arr) - 1 # np.count_nonzero(arr)) 统计非0元素的个数
else:
neighbor_live_num = np.count_nonzero(arr)
if neighbor_live_num == 2:
next_status = crrent_status
elif neighbor_live_num == 3:
next_status = 1
else:
next_status = 0
return next_status
def origin_to_extend(source):
'''
将源二维数组的外围添加一圈邻居,数值填充为0,作为哨兵,以防止判断外圈单元格时出现下标越界
:param source: 源二维数组
:return: 扩充后的二维数组
'''
m,n = source.shape
res = np.zeros((m+2,n+2))
res[1:m+1,1:n+1] = source
return res
def draw_x_life_game(arr,x,size):
'''
绘制x次迭代的生命游戏的世界
:return:
'''
now = arr
draw(now, -450, 0, size) # 绘制当前状态
for k in range(x):
#计算下一代
next_time = now
ex_now = origin_to_extend(now)
m, n = now.shape
for i in range(m):
for j in range(n):
next_time[i,j] = live_or_die(ex_now[i:i+3,j:j+3])
# print(next_time)
draw(next_time, -450 + (size * (n + 1))*(k+1), 0, size)
now = next_time
def main():
now = np.array([[0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0],
])
# now = np.eye(11,11)
draw_x_life_game(now, 4,20)
#保存图片
ts = turtle.getscreen()
ts.getcanvas().postscript(file="3.eps")
turtle.done()
if __name__ == '__main__':
main()
结果:

这个在书中被叫做吞噬者,因为随着迭代的进行,左下方的形状会把右上角的形状吞噬掉?。
解释:
通过修改main()函数中的now二维数组的输入,以及修改
89行 draw_x_life_game(now, 4,20)中的第二个参数(迭代次数),第三个参数(小正方形的边长)可以绘制其他不同的情况
如:
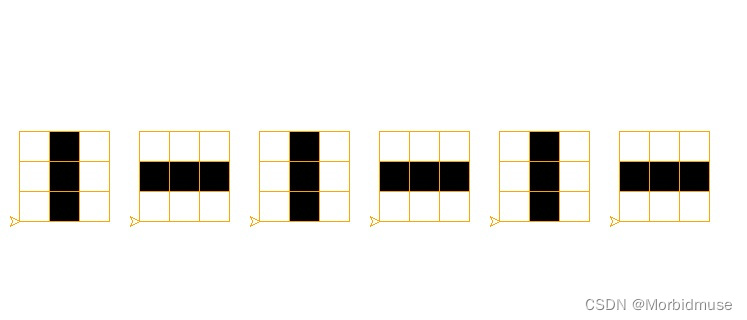
信号灯:两代之间交替
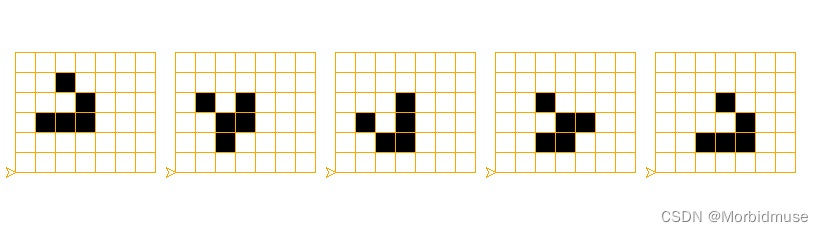
?滑翔机:经过4代又回到原来的形状,就像从开始位置滑翔到了终止位置
静止的生命:保持不变
 ?
?
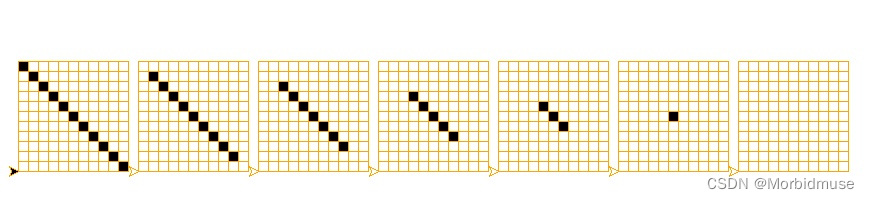
消失的斜线
 ?
?
?
补充:
最后的保存图片为eps格式,可以通过ps打开

?如果使用.jpg会因为信息丢失无法打开
35岁学python,也不知道为了啥