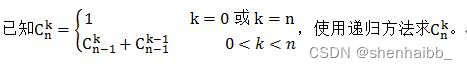文章目录
算法训练
ALGO-92-前缀表达式
【问题描述】
编写一个程序,以字符串方式输入一个前缀表达式,然后计算它的值。输入格式为:“运算符 对象1 对象2”,其中,运算符为“+”(加法)、“-”(减法)、“*”(乘法)或“/”(除法),运算对象为不超过10的整数,它们之间用一个空格隔开。要求:对于加、减、乘、除这四种运算,分别设计相应的函数来实现。
输入格式:输入只有一行,即一个前缀表达式字符串。
输出格式:输出相应的计算结果(如果是除法,直接采用c语言的“/”运算符,结果为整数)。
【样例输入】
+ 5 2
【样例输出】
7
刚开始还以为很长的前缀表达式字符串,要计算它的值,后来发现就输入三个对象就行了。。。。。
注意,用‘/’号的时候,结果要返回为整数
S = list(input().split())
print(int(eval(S[1] + S[0] + S[2])))
ALGO-95-2的次幂表示
【问题描述】
任何一个正整数都可以用2进制表示,例如:137的2进制表示为10001001。
将这种2进制表示写成2的次幂的和的形式,令次幂高的排在前面,可得到如下表达式:137=27+23+2^0
现在约定幂次用括号来表示,即a^b表示为a(b)
此时,137可表示为:2(7)+2(3)+2(0)
进一步:7=22+2+20 (2^1用2表示)
3=2+2^0
所以最后137可表示为:2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:1315=210+28+2^5+2+1
所以1315最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
【输入格式】
正整数(1<=n<=20000)
【输出格式】
符合约定的n的0,2表示(在表示中不能有空格)
【样例输入】
137
【样例输出】
2(2(2)+2+2(0))+2(2+2(0))+2(0)
【样例输入】
1315
【样例输出】
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
def show(num):
if num == 1:
print('2', end='')
else:
print(f'2({num})', end='')
def fun(arr, m):
# 先给出m的二进制(在这里我没用python自带函数)
bin_arr = []
while m:
bin_arr.insert(0, m % 2)
m //= 2
bin_arr.reverse()
# 根据二进制数组获得次幂数数组
for i in range(len(bin_arr)):
if bin_arr[i] == 1:
arr.append(i)
arr.reverse()
# 遍历次幂数数组
for i in range(len(arr)):
if i != 0:
print('+', end='')
if arr[i] <= 2:
# 如果小于等于2,则输出
show(arr[i])
else:
# 否则递归,外面需要套上2()
print('2(', end='')
fun([], arr[i])
print(')', end='')
if __name__ == '__main__':
n = int(input())
fun([], n)
ALGO-122-未名湖边的烦恼
【问题描述】
每年冬天,北大未名湖上都是滑冰的好地方。北大体育组准备了许多冰鞋,可是人太多了,每天下午收工后,常常一双冰鞋都不剩。
每天早上,租鞋窗口都会排起长龙,假设有还鞋的m个,有需要租鞋的n个。现在的问题是,这些人有多少种排法,可以避免出现体育组没有冰鞋可租的尴尬场面。(两个同样需求的人(比如都是租鞋或都是还鞋)交换位置是同一种排法)
【输入格式】
两个整数,表示m和n
【输出格式】
一个整数,表示队伍的排法的方案数。
【样例输入】
3 2
【样例输出】
5
之前一直没懂这题说的什么,后来是看了大佬的博客才了解这道题的解法,采用递归的思想
传送门:算法训练 未名湖边的烦恼_@Star的博客
python版代码如下:
def fun(m, n):
# 如果还鞋的人 < 租鞋的人,说明无鞋可租,不能这样排
if m < n:
return 0
# 当没人租鞋的时候,也可以算是一种方法
if n == 0:
return 1
# '还鞋的人在后面,租鞋的人在前面' 或 '租鞋的人在后面,还鞋的人在前面' 都可以接着排序
return fun(m - 1, n) + fun(m, n - 1)
if __name__ == '__main__':
# m:还鞋 n:租鞋
m, n = list(map(int, input().split()))
print(fun(m, n))
ALGO-150-递归求二项式系数值
【问题描述】
【样例输入】
3 10
【样例输出】
120
def fun(k, n):
if k == 0 or k == n:
return 1
return fun(k, n - 1) + fun(k - 1, n - 1)
if __name__ == '__main__':
k, n = list(map(int, input().split()))
print(fun(k, n))
ALGO-449-递归输出数字三角形
【问题描述】
输出一个n行的与样例类似的数字三角形,必须使用递归来实现
【输入格式】
一个正整数数n,表示三角形的行数
【输出格式】
输出一个与样例类似的n行的数字三角形,同一行每两个数之间用一个空格隔开即可(图中只是为防止题面格式化而用’_'代替空格)
【样例输入】
4
【样例输出】
___1
__2_3
_4_5_6
7_8_9_10
def show(arr):
# 判断前面打印多少个空格
print(' ' * abs(len(arr) - n), end='')
for i in arr:
print(i,end=' ')
print('')
def fun(start, step):
# 如果步数为n+1,则返回,步数为n时,还得继续递归
if step == n + 1:
return
# 输出这段数组的内容
show(arr[start:start + step])
# 起点为start + step,步数为step + 1
fun(start + step, step + 1)
if __name__ == '__main__':
n = int(input())
# 初始化数组,从1开始
arr = [i + 1 for i in range(int((1 + n) * n / 2))]
# 起点为0,步数为1
fun(0, 1)
ALGO-487-整数循环
【问题描述】
编写一个程序,输入一个4位的正整数,将组成该数的各位数字重新排列,形成一个最大数和一个最小数,之后用最大数减去最小数,得到一个新的正整数(该数一定大于1000)。然后对于这个新的正整数,重复上述步骤,直到该正整数的值不再发生变化。
例如,假设用户输入的正整数为1001,那么由它所形成的最大数为1100,最小数为11,因此新的正整数为1089。对于1089,由它形成的最大数为9810,最小数为189,因此新的正整数为9621。9621的最大数为9621,最小数为1269,结果为8352,。8352的最大数为8532,最小数为2358,结果为6174。6174的最大数为7641,最小数为1467,结果仍为6174,因此程序结束。(注:出自课本第六章第22题)
【样例输入】
1001
【样例输出】
6174
n = input()
temp = int(n)
# 如果n不等于temp,则循环一直继续
while n != temp:
temp = n # 用来判断n的值是否改变
# 先将数组转为字符串,再转换成数组,再升序排列,再转换成字符串
max_num = ''.join(sorted(list(str(n)), reverse=True))
# 先将数组转为字符串,再转换成数组,再降序排列,再转换成字符串
min_num = ''.join(sorted(list(str(n)), reverse=False))
# 相减时需要转换成int类型
n = int(max_num) - int(min_num)
print(n)
ALGO-532-数的计数
【问题描述】
我们要求找出具有下列性质数的个数(包含输入的自然数n):
先输入一个自然数n(n<=1000),然后对此自然数按照如下方法进行处理:
1. 不作任何处理;
2. 在它的左边加上一个自然数,但该自然数不能超过原数的一半;
3. 加上数后,继续按此规则进行处理,直到不能再加自然数为止.
【输入格式】
一个数n
【输出格式】
一个数表示答案
【样例输入】
6
【样例输出】
6
【样例说明】
满足条件的数为6,16,26,126,36,136
刚开始还每个都打印输出,后来发现只要计数就行了
def fun(m):
global count
if m == 1:
return
count += int(m / 2) # 数的一半有多少个 就有多少种
# 遍历数的一半,递归执行函数
for i in range(1, int(m / 2) + 1):
fun(i)
if __name__ == '__main__':
n = int(input())
count = 1 # 数本身也是一种
fun(n)
print(count)
ALGO-573-计算最小公倍数
【问题描述】
接收用户输入的自然数m,n,计算它们的最小公倍数。
【样例输入】
4 6
【样例输出】
12
这里记录一下最大公约数和最小公倍数的求法,做十次,十次都不记得过程。。
# 最大公约数greatest common divisor
def gcd(a, b):
if a < b:
a, b = b, a
if b == 0:
return a
return gcd(b, a % b)
# 最小公倍数least common multiple
def lcm(a, b):
remainder = gcd(a, b)
print(int(a * b / remainder))
if __name__ == '__main__':
m, n = input().split()
lcm(int(m), int(n))
ALGO-605-分解质因数
【问题描述】
求出区间[a,b]中所有整数的质因数分解。
【输入格式】
输入两个整数a,b。
【输出格式】
每行输出一个数的分解,形如k=a1a2a3…(a1<=a2<=a3…,k也是从小到大的)(具体可看样例)
【样例输入】
3 10
【样例输出】
3=3
4=22
5=5
6=23
7=7
8=222
9=33
10=25
还有一题也是质因数的,可以一起做
# 获取一个数的质因数
def get_list(n):
i = 2
arr = []
while i <= n:
if n % i == 0:
arr.append(f'{i}') # 因为想用join()函数,所以数组里面存放的是字符串类型
n /= i
else:
i += 1
return arr
if __name__ == '__main__':
a, b = input().split()
for i in range(int(a), int(b) + 1):
print(f'{i}=', end='')
print('*'.join(get_list(i)))
ALGO-618-级数求和
【问题描述】
已知:Sn= 1+1/2+1/3+…+1/n。显然对于任意一个整数K,当n足够大的时候,Sn大于K。
现给出一个整数 K,要求计算出一个最小的n;使得Sn>K。
【输入格式】
一个整数,表示整数 k
【输出格式】
一个整数,表示最小的n
【样例输入】
1
【样例输出】
2
k = int(input())
Sn = 0
n = 1
while True:
Sn += (1 / n)
if Sn > k:
break
n += 1
print(n)
ALGO-645-加法分解
【问题描述】
给一个正整数n,输出它所有的正整数加法的分解方法。
注意:
1. 根据输入的要求决定交换加数的位置是否视为不同的分解方案。
2. 不分解也视为一种分解方案。
3. 按字典序输出所有分解方案,格式见样例。
【输入格式】
输入共1行,包含2个正整数n和m,之间用一个空格隔开。n表示待分解正整数,m是1或者2:
1表示交换加数的位置是否视为不同的分解方案;
2表示交换加数的位置是否视为相同的分解方案。
【输出格式】
输出若干行,每行表示一种分解方案。对于一种方案,先输出n,再输出一个“=”。然后输出分解的各数,不同的数之间用一个“+”连接。
【样例输入】
5 2
【样例输出】
5=1+1+1+1+1
5=1+1+1+2
5=1+1+3
5=1+2+2
5=1+4
5=2+3
5=5
【样例输入】
5 1
【样例输出】
5=1+1+1+1+1
5=1+1+1+2
5=1+1+2+1
5=1+1+3
5=1+2+1+1
5=1+2+2
5=1+3+1
5=1+4
5=2+1+1+1
5=2+1+2
5=2+2+1
5=2+3
5=3+1+1
5=3+2
5=4+1
5=5
def show(arr):
# 输出第一个值
print(f'{n}={arr[0]}', end='')
# 之后每个值输出前都加上'+'号
for i in arr[1:]:
print(f'+{i}', end='')
print('')
def dfs(first_num, end, count):
'''
:param first_num: 第一个数从多少开始
:param end: 数组最后一个索引
:param count: 累计和
:return:
'''
# 和大于输入的n,则返回
if count > n:
return
# 和等于输入的n,则输出
if count == n:
show(arr[:end])
return
# 和小于输入的n,则继续下面的步骤
# 判断m为1还是2,差别在于从几开始循环,一个从1开始,一个从first_num开始
if m == 1:
for i in range(1, n + 1):
arr[end] = i # 数组索引的最后一个数为i
# 递归,从i开始,end往后移一位,累计和加上当前i
dfs(i, end + 1, count + i)
elif m == 2:
for i in range(first_num, n + 1):
arr[end] = i
dfs(i, end + 1, count + i)
if __name__ == '__main__':
n, m = list(map(int, input().split()))
arr = [0 for _ in range(n)]
dfs(1, 0, 0)
ALGO-682-求先序排列
【问题描述】
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,长度<=8)。
【输入格式】
两行,每行一个字符串,分别表示中序和后序排列
【输出格式】
一个字符串,表示所求先序排列
【样例输入】
BADC
BDCA
【样例输出】
ABCD
解析见 ALGO-705-根据前、中序遍历求后序遍历
def fun(LDR, LRD):
if LDR == LRD and len(LDR) < 1:
print(LDR, end='')
return
D = LRD[-1]
print(D, end='')
L = LDR.split(D)[0]
fun(L, LRD[:len(L)])
R = LDR.split(D)[1]
fun(R, LRD[len(L):-1])
if __name__ == '__main__':
LDR = input() # 中序遍历序列
LRD = input() # 后序遍历序列
fun(LDR, LRD)
ALGO-705-根据前、中序遍历求后序遍历
【问题描述】
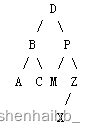
给定一棵二叉树的前序遍历和中序遍历序列,用你所熟悉的程序设计语言生成该二叉树,并将其后序遍历打印出来。为便于编程,二叉树的结点用单个大写英文字母表示,且结点互不重复。比如,输入前序遍历序列为DBACPMZX,中序遍历序列为ABCDMPXA,应生成的二叉树结构如下图所示:
应输出的后序遍历序列为ACBMXZPD
【输入格式】
两行两个大写字母字符串,分别代表前序和中序遍历
【输入格式】
一行表示后序遍历
【样例输入】
DBACPMZX
ABCDMPXZ
【样例输出】
ACBMXZPD
前提知识:
先序遍历序列:根左右
中序遍历序列:左根右
后序遍历序列:左右根
题目:
先序遍历序列:D BACPMZX
中序遍历序列:ABC D MPXZ
这题想到用递归,递归出口就是先序遍历序列等于中序遍历序列的时候,说明只有一个字符
我们根据先序遍历序列获取根结点:D
根据 ‘中序遍历序列:左根右’ 的知识,我们可以知道用根结点分割中序遍历序列时,分割成两个部分,第一个部分是左子树,第二部分是右子树
[‘ABC’, ‘D’, ‘MPXZ’] ==> 左子树:‘ABC’ 右子树:‘MPXZ’
然后开始递归,这里递归的顺序是,先递归左子树,再递归右子树
1、先递归左子树
获取左子树的先序遍历序列和中序遍历序列,递归fun函数
- 先序遍历序列:DLR[1:len(L) + 1]
(第一个是根结点,因此从1开始,直到左子树的长度+1,作为左子树的先序遍历序列)
- 中序遍历序列:L
(左子树是从中序遍历序列中获得的,作为左子树的中序遍历序列)
2、再递归右子树
获取右子树的先序遍历序列和中序遍历序列,递归fun函数
- 先序遍历序列:DLR[len(L) + 1:]
(从左子树的长度+1开始直到结尾,作为右子树的先序遍历序列)
- 中序遍历序列:R
(右子树是从中序遍历序列中获得的,作为右子树的中序遍历序列)
3、最后输出根结点
根结点就是先序遍历序列的第一个值,即DLR[0]
def fun(DLR, LDR):
# 如果先序遍历序列 == 中序遍历序列,且只有一个字符,可以直接输出
if DLR == LDR and len(LDR) < 1:
print(DLR, end='')
return
D = DLR[0] # 获取根结点
# 1、先递归左子树
# 根据根结点进行分割中序遍历序列,第0个是左子树
L = LDR.split(D)[0]
# 递归:先序遍历序列为DLR[1:len(L) + 1],后序遍历序列为L
fun(DLR[1:len(L) + 1], L)
# 2、再递归右子树
# 根据根结点进行分割中序遍历序列,第1个是右子树
R = LDR.split(D)[1]
# 递归:先序遍历序列为DLR[len(L) + 1:],后序遍历序列为R
fun(DLR[len(L) + 1:], R)
# 3、最后输出根结点
print(D, end='') # 输出根结点,因为后序遍历序列是左右根,根结点在最后
if __name__ == '__main__':
DLR = input() # 先序遍历序列
LDR = input() # 中序遍历序列
fun(DLR, LDR)
ALGO-934-序列
【问题描述】
王神想要知道n的所有排列的逆序对数和,但是他觉得太水了,于是让你算。
【输入格式】
一行一个整数n
【输出格式】
一行即答案,对1007取模
【样例输入】
2
【样例输出】
1
刚开始看这道题又没看懂(我理解能力是真的差),后来搜了一下看到了这篇博客下的博主评论,才知道要先求全排列,再求逆序数
传送门:试题 算法训练 序列_@醉尘归的博客
这道题就转变成如下两步:
1、求一个数的全排列
2、求全排列的逆序数
全排列b站讲解:【python】递归与回溯-全排列(第二讲)_@八月里的小太阳
逆序数b站讲解:【XDOJ】1052:经典逆序对问题【Python基础系列习题学习教程】_@散装未央
python代码如下:
# 求逆序数
def inverse_num(arr):
# 设置count为全局变量
global count
# 新建一个同等长度的全0数组
arr_temp = [0 for _ in range(len(arr))]
# 遍历原数组
for i in arr:
arr_temp[i - 1] += 1
count += sum(arr_temp[i:])
# 求全排列
def permutation(m):
if len(visited) == n:
# 计算该数组的逆序数
inverse_num(visited)
return
# 因为求全排列,所以要遍历1~n
for i in range(1, n + 1):
if i not in visited:
visited.append(i)
permutation(i) # 递归
visited.remove(i) # 回溯
if __name__ == '__main__':
n = int(input())
count = 0 # 计算逆序数的个数
# 先计算一个数的全排列
arr = [i + 1 for i in range(n)]
visited = []
permutation(arr)
# 打印个数
print(count % 1007)
ALGO-940-试题3971
【问题描述】
有一些正整数,如果这个正整数分解质因数之后,只包含2或3或5,那么该数即为“丑数”,比如100就是“丑数”,100分解质因数之后只包含2和5;14就不是“丑数”,因为14分解质因数之后,包含了7.
输入正整数n,请写程序判断n是否是“丑数”,是“丑数”则输出“yes”,否则输出“no”。
【输入格式】
一个正整数n
【输出格式】
一个字符串yes 或no
【样例输入】
15
【样例输出】
yes
【样例输入】
242
【样例输出】
no
先求一个数的分解质因数,分解质因数不知道什么概念的同学(比如说我)可以先上网查一下相关资料
然后遍历,看是不是有除了2、3、5之外的数,没有的话就是丑,有的话就不是丑数
这里要注意的是要限制n>2,1和2都不是丑数
因为1只能被分解为1 * 1
2只能被分解为1 * 2
# 求一个数的分解质因数
def get_list(n):
i = 2
list1 = []
while i <= n:
if n % i == 0:
list1.append(i)
n /= i
else:
i += 1
return list1
if __name__ == '__main__':
n = int(input())
list1 = get_list(n)
flag = True # 设置一个标识
for i in list1:
if i != 2 and i != 3 and i != 5:
flag = False
break
# 判断flag,如果为真,则为丑数,否则不是丑数
if flag and n > 2:
print("yes")
else:
print("no")
ALGO-951-预备爷的悲剧
【问题描述】
英语预备爷gzp是个逗(tu)比(hao),为了在即将到来的英语的quiz中不挂科,gzp废寝忘食复习英语附录单词表,俨然一场人间悲剧。不过上天有好生之德,上帝扔给了gzp一张纸,上面记载了将要考到的单词。不过gzp是个逗比,之前复习的东西全忘记了,所以他又要再来一次复习。不过已经知道了要考的单词,所以不需要复习单词表的所有页数。因此,现在需要你帮助他求出有多少页纸需要复习。他会告诉你每个单词会在哪几页出现,并且告诉你要考哪些单词,你只要告诉他答案就可以了。由于一个单词会出现在不同页上,只需要复习在最前面一页上的就可以了。
【输入格式】
第一行一个整数n,表示单词附录有n个单词。接下来n行每行一个小写字母组成的单词和一个整数,表示某一个单词和它所在的页数。接下来是一行整数m,表示要考m个单词,接下来m行小写字母组成的单词,表示要考到的单词。
【输出格式】
一个数,表示需要复习的页数。
【样例输入】
5
ab 1
ac 2
ab 2
ac 3
c 3
3
ab
ac
c
【样例输出】
3
其实这题并不难,但缺少训练的我还是做了很久!哭
刚开始没想到用字典,原本想用二维数组,先存起来,最后遍历判断,结果运行超时,晕
看了大佬的博客,恍然大悟,原来我一直把题目理解错了,我以为最多看到多少页。。。
大佬传送门:Python蓝桥杯算法训练—预备爷的悲剧_@Py小郑
做了这道题给我的感受就是字典真是个好东西啊
另外有个坑,就是判断一个数是否在字典内时,我用的是 if arr_n.get(word):,导致最后只有80分,后来变成了if word in arr_n:,就通过了。现在也没想明白是为啥
python代码如下:
n = int(input()) # 输入n行以及这n个附录单词和它所在的页数
arr_n = {} # 创建键值对
for i in range(n):
word, page = input().split()
# 先查看该单词是否出现在字典里
# 1)若出现过,则判断是否要更新页数(因为题目说只需要复习最前面的一页就可以)
# 2)若没出现过,则添加键值对
if word in arr_n:
# 保留页数较小的
if arr_n.get(word) > int(page):
arr_n[word] = int(page)
else:
arr_n[word] = int(page)
m = int(input()) # 输入m行以及这m个要考的单词
arr_m = [] # 创建数组
for i in range(m):
arr_m.append(input())
# 遍历要考的单词,获得其页数,存入数组
pages = []
for i in arr_m:
pages.append(arr_n.get(i))
# 最后数组去重
print(len(set(pages)))
ALGO-976-P0804
【问题描述】
编写一个函数void strcompress(char *s),输入一个字符串(只包含小写字母和空格,且长度小于1000),然后采用如下的规则对该字符串当中的每一个字符进行压缩:
(1) 如果该字符是空格,则保留该字符。
(2) 如果该字符是第1次出现或第3次出现或第6次出现,则保留该字符。
(3) 否则,删除该字符。
例如,若用户输入occurrence,经过压缩后,字符c的第2次出现被删除,第1和第3次出现仍保留;字符r和e的第2次出现均被删除,因此最后的结果为:ocurenc。
编写main函数测试该函数的正确性。
【输入格式】
occurrence
【输出格式】
ocurenc
刚开始没有判断字符是不是空字符串,导致得分只有20分,我恨,审题不仔细
n = list(input())
arr = [0 for _ in range(26)] # 定义一个26个字母长的全0数组
for i in range(len(n)):
# 先判断字符是不是空格
# 1) 如果是空格,则什么都不做,保留字符
# 2) 如果不是空格,则继续判断
if n[i] != ' ':
# 根据字符串中的字符,记录出现的一次,出现一次,arr数组对应的值加1
arr[ord(n[i]) - ord('a')] += 1
# 判断字符在arr数组中对应的值是否是1、3、6,如果不是,则说明要删除,先赋值为'-'
if arr[ord(n[i]) - ord('a')] not in [1, 3, 6]:
n[i] = '-'
# 将n数组先变成字符串,然后根据'-'字符进行分割,又变成了数组
n = ''.join(n).split('-')
# 将数组打印成字符串,变成最终输出
print(''.join(n))
ALGO-992-士兵杀敌(二)
【问题描述】
南将军手下有N个士兵,分别编号1到N,这些士兵的杀敌数都是已知的。
小工是南将军手下的军师,南将军经常想知道第m号到第n号士兵的总杀敌数,请你帮助小工来回答南将军吧。
南将军的某次询问之后士兵i可能又杀敌q人,之后南将军再询问的时候,需要考虑到新增的杀敌数。
【输入格式】
多组测试数据,以EOF结尾;
每组第一行是两个整数N,M,其中N表示士兵的个数(1<N<1000000),M表示指令的条数。(1<M<100000)
随后的一行是N个整数,ai表示第i号士兵杀敌数目。(0<=ai<=100)
随后的M行每行是一条指令,这条指令包含了一个字符串和两个整数,首先是一个字符串,如果是字符串QUERY则表示南将军进行了查询操作,后面的两个整数m,n,表示查询的起始与终止士兵编号;如果是字符串ADD则后面跟的两个整数I,A(1<=I<=N,1<=A<=100),表示第I个士兵新增杀敌数为A.
【输出格式】
对于每次查询,输出一个整数R表示第m号士兵到第n号士兵的总杀敌数,每组输出占一行
【样例输入】
5 6
1 2 3 4 5
QUERY 1 3
ADD 1 2
QUERY 1 3
ADD 2 3
QUERY 1 2
QUERY 1 5
【样例输出】
6
8
8
20
这题我第一眼看的时候好长,就不想看了。仔细一看,其实逻辑都挺简单的
但是这里有一个坑,导致我最后得分0分
就是题目中说到 多组测试数据,以EOF结尾
我上网搜,才知道这个原来是要有固定格式的
传送门:Python - 以EOF结束循环的方法@_陈 零.
try:
while True:
N, M = list(map(int, input().split()))
arr = list(map(int, input().split()))[:N]
for i in range(M):
Command, a, b = input().split()
a, b = int(a), int(b)
if Command == 'QUERY':
print(sum(arr[a - 1:b]))
elif Command == 'ADD':
arr[a - 1] += b
except:
pass
算法提高
PREV-281-时间显示
【问题描述】
小蓝要和朋友合作开发- -个时间显示的网站。在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从1970年1月1日00:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
【输入格式】
输入一行包含一个整数,表示时间。
【输出格式】
输出时分秒表示的当前时间,格式形如HH:MM:SS,其中HH表示时,值为0到23,MM表示分,值为0到59,Ss表示秒,值为0到59。时、分、秒
不足两位时补前导0.
【样例输入1】
46800999
【样例输出1】
13:00:00
【样例输入2】
1618708103123
【样例输出2】
01:08:23
竟然记成一秒=60毫秒了 我说怎么样例半天算不对。。
思路:先定义一天、一小时、一分钟、一秒的毫秒数
再取余数算出一天内的时间
再算出多少小时、多少分钟、多少秒
最后格式化输出(格式化输出需要字符串类型),前面补两位数
n = int(input())
one_day = 24 * 60 * 60 * 1000
one_hour = 60 * 60 * 1000
one_minute = 60 * 1000
one_second = 1000
n %= one_day
hour = int(n / one_hour) # 小时
minute = int((n - hour * one_hour) / one_minute) # 分钟
second = int((n - hour * one_hour - minute * one_minute)/ one_second) # 秒
print(f'{str(hour).zfill(2)}:{str(minute).zfill(2)}:{str(second).zfill(2)}') # 格式化输出
?