1.基础知识与安装
import torch
torch.__version__
'1.10.2+cpu'
本机为ATI显卡,无法支持CUDA,特使用CPU版本
torch.cuda.is_available()
False
Tensor 是深度学习框架中极为基础的概念,也是 PyTroch、TensorFlow 中最重要的知识点之一,它是一种数据的存储和处理结构。
1.标量,也称 Scalar,是一个只有大小,没有方向的量,比如 1.8、e、10 等。
2.向量,也称 Vector,是一个有大小也有方向的量,比如 (1,2,3,4) 等。
3.矩阵,也称 Matrix,是多个向量合并在一起得到的量,比如[(1,2,3),(4,5,6)]等。
标量可以组合成向量,向量可以组合成矩阵。在 PyTorch 中我们称之为张量 (Tensor)。
我们更愿意使用 Rank(秩)来表示这种“维度”,比如标量,就是 Rank 为 0 阶的 Tensor;向量就是 Rank 为 1 阶的 Tensor;矩阵就是 Rank 为 2 阶的 Tensor。也有 Rank 大于 2 的 Tensor。
在 PyTorch 中,Tensor 支持的数据类型有很多种,这里列举较为常用的几种格式:
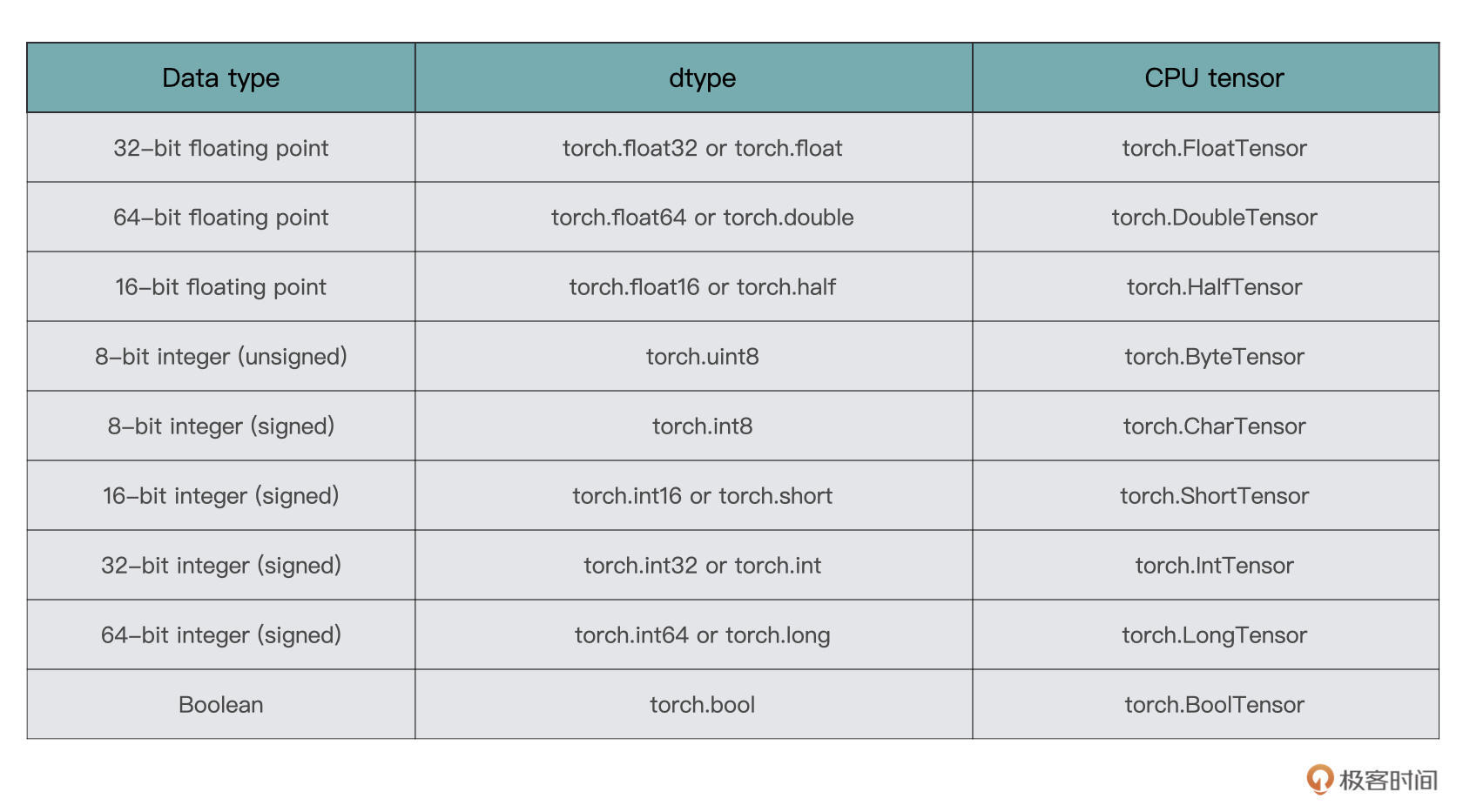
2.创建Tensor
从Numpy创建:
import numpy as np
arr = np.asarray([[1, 2], [3, 4]])
arr
array([[1, 2],
[3, 4]])
torch.from_numpy(arr)
tensor([[1, 2],
[3, 4]], dtype=torch.int32)
创建随机张量:
x = torch.rand(4, 3)
print(x)
tensor([[0.7571, 0.6708, 0.5150],
[0.9366, 0.0267, 0.2567],
[0.0569, 0.1151, 0.5494],
[0.5117, 0.2451, 0.7550]])
x = torch.randn(4, 3)
print(x)
tensor([[-0.4653, 1.2740, -1.2445],
[ 1.2446, -1.7297, -0.3737],
[-0.0197, -0.5678, -1.0294],
[-1.5619, -0.1930, 1.5858]])
torch.randint(1, 100,(4,3))
tensor([[82, 9, 43],
[47, 10, 79],
[ 2, 59, 41],
[83, 96, 32]])
torch.rand 用于生成数据类型为浮点型且维度指定的随机 Tensor,随机生成的浮点数据在 0~1 区间均匀分布。
torch.randn 用于生成数据类型为浮点型且维度指定的随机 Tensor,随机生成的浮点数的取值满足均值为 0、方差为 1 的标准正态分布。
torch.normal 用于生成数据类型为浮点型且维度指定的随机 Tensor,可以指定均值和标准差
torch.randint 用于生成随机整数的 Tensor,其内部填充的是在[low,high) 均匀生成的随机整数。
torch.normal(0, 1, (4,3))
tensor([[-0.9910, 0.0434, -0.6888],
[ 0.8102, 0.7988, 1.2313],
[ 0.8767, -0.1450, -0.3473],
[-0.0999, 0.9080, 0.5567]])
创建零矩阵Tensor:所有的元素都为 0 的矩阵
x = torch.zeros(4, 3, dtype=torch.long)
print(x)
tensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
创建单位矩阵 Tensor:单位矩阵是指主对角线上的元素都为 1 的矩阵。
x = torch.eye(4, 3, dtype=torch.long)
print(x)
tensor([[1, 0, 0],
[0, 1, 0],
[0, 0, 1],
[0, 0, 0]])
x = torch.eye(3, 4, dtype=torch.long)
print(x)
tensor([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0]])
创建全一矩阵 Tensor:所有的元素都为 1 的矩阵。
x = torch.ones(3, 4, dtype=torch.long)
print(x)
tensor([[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]])
3.Tensor的转换
在这里对于一个 list a,我们仍旧直接使用 torch.Tensor,就可以将其转换为 Tensor 了。而还原回来的过程要多一步,需要我们先将 Tensor 转为 NumPy 结构,之后再使用 tolist() 函数得到 list。
a = [1, 2, 3]
b = torch.tensor(a)
c = b.numpy().tolist()
a
[1, 2, 3]
b
tensor([1, 2, 3])
c
[1, 2, 3]
x
tensor([[-0.4653, 1.2740, -1.2445],
[ 1.2446, -1.7297, -0.3737],
[-0.0197, -0.5678, -1.0294],
[-1.5619, -0.1930, 1.5858]])
获取张量的形状:
x.shape
torch.Size([4, 3])
x.size()
torch.Size([4, 3])
使用 numel() 函数直接统计元素数量:
x.numel()
12
在 PyTorch 中有两个函数,分别是 permute() 和 transpose() 可以用来实现矩阵的转秩,或者说交换不同维度的数据。比如在调整卷积层的尺寸、修改 channel 的顺序、变换全连接层的大小的时候,我们就要用到它们。
x = torch.rand(2,3,5)
x
tensor([[[0.1471, 0.3936, 0.4790, 0.5673, 0.9295],
[0.4615, 0.1967, 0.8750, 0.9002, 0.3955],
[0.2762, 0.5876, 0.0417, 0.7652, 0.6760]],
[[0.4625, 0.0234, 0.8368, 0.9084, 0.5178],
[0.0163, 0.8012, 0.9679, 0.2990, 0.9299],
[0.4314, 0.9663, 0.4993, 0.5329, 0.3811]]])
x.shape
torch.Size([2, 3, 5])
x = x.permute(2,1,0)
x
tensor([[[0.1471, 0.4625],
[0.4615, 0.0163],
[0.2762, 0.4314]],
[[0.3936, 0.0234],
[0.1967, 0.8012],
[0.5876, 0.9663]],
[[0.4790, 0.8368],
[0.8750, 0.9679],
[0.0417, 0.4993]],
[[0.5673, 0.9084],
[0.9002, 0.2990],
[0.7652, 0.5329]],
[[0.9295, 0.5178],
[0.3955, 0.9299],
[0.6760, 0.3811]]])
x.shape
torch.Size([5, 3, 2])
有时候我们需要对 Tensor 增加或者删除某些维度,比如删除或者增加图片的几个通道。PyTorch 提供了 squeeze() 和 unsqueeze() 函数解决这个问题。
x = torch.rand(2,1,3)
x
tensor([[[0.0450, 0.6442, 0.8720]],
[[0.1986, 0.4911, 0.4109]]])
x.shape
torch.Size([2, 1, 3])
y = x.squeeze(1)
y.shape
torch.Size([2, 3])
z = y.squeeze(1)
z.shape
torch.Size([2, 3])
如果 dim 指定的维度的值为 1,则将该维度删除,若指定的维度值不为 1,则返回原来的 Tensor。
unsqueeze():这个函数主要是对数据维度进行扩充,给指定位置加上维数为 1 的维度。
x = torch.rand(2,1,3)
y = x.unsqueeze(2)
y
tensor([[[[0.8471, 0.4028, 0.2251]]],
?
[[[0.2698, 0.2658, 0.6385]]]])
4.广播运算
当对两个形状不同的 Tensor 按元素运算时,可能会触发广播(broadcasting)机制:先适当复制元素使这两个 Tensor 形状相同后再按元素运算。
x = torch.rand(2,1,3)
x
tensor([[[0.9263, 0.0624, 0.8228]],
[[0.2334, 0.3812, 0.0049]]])
x + 1
tensor([[[1.9263, 1.0624, 1.8228]],
[[1.2334, 1.3812, 1.0049]]])
x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)
tensor([[1, 2]])
tensor([[1],
[2],
[3]])
tensor([[2, 3],
[3, 4],
[4, 5]])
5.自动求导
在张量创建时,通过设置 requires_grad 标识为Ture来告诉Pytorch需要对该张量进行自动求导,PyTorch会记录该张量的每一步操作历史并自动计算
x = torch.rand(5, 5, requires_grad=True)
x
tensor([[0.8205, 0.7034, 0.2400, 0.3493, 0.0921],
[0.7301, 0.1440, 0.8934, 0.1666, 0.4757],
[0.9641, 0.8949, 0.6069, 0.4763, 0.1363],
[0.9504, 0.8406, 0.8181, 0.1522, 0.4108],
[0.3150, 0.6705, 0.0365, 0.6964, 0.7752]], requires_grad=True)
y = torch.rand(5, 5, requires_grad=True)
y
tensor([[0.5807, 0.4427, 0.1541, 0.1270, 0.2581],
[0.5497, 0.7469, 0.5976, 0.1933, 0.8360],
[0.9181, 0.6554, 0.1375, 0.9361, 0.8990],
[0.7945, 0.0196, 0.2215, 0.7029, 0.2584],
[0.9604, 0.9870, 0.7703, 0.7432, 0.6213]], requires_grad=True)
PyTorch会自动追踪和记录对与张量的所有操作,当计算完成后调用.backward()方法自动计算梯度并且将计算结果保存到grad属性中。
print(y.grad_fn)
<AddBackward0 object at 0x000001B65542FA90>
z=torch.sum(x+y)
z
tensor(27.4705, grad_fn=<SumBackward0>)
在张量进行操作后,grad_fn已经被赋予了一个新的函数,这个函数引用了一个创建了这个Tensor类的Function对象。 Tensor和Function互相连接生成了一个非循环图,它记录并且编码了完整的计算历史。每个张量都有一个.grad_fn属性,如果这个张量是用户手动创建的那么这个张量的grad_fn是None。
z.backward()
print(x.grad,y.grad)
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]]) tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
如果Tensor类表示的是一个标量(即它包含一个元素的张量),则不需要为backward()指定任何参数,但是如果它有更多的元素,则需要指定一个gradient参数,它是形状匹配的张量。