目录
目录
一、背景
例如，煤岩在真三轴分级循环中间主应力
条件下除了会产生残余变形现象外，循环加–卸载曲线还会产生
塑性滞回环
的现象，而残余变形只能反映加–卸载点处的塑性变形量，塑性滞回环的
面积
则能反映整个加卸载过程中耗散的能量，耗散能可表征整个循环加卸载过程中煤岩损失的能量。因此，有必要将
每次循环过程中产生的耗散能或损伤进行详细分析。
二、试验数据
数据由
QKX-ZSZ-4000岩体真三轴动静载荷试验仪器（11W条数据）导出，可以容易得到一系列应力应变值，绘制
应力应变曲线可以得到如下图。从该图可以看出，一些列的循环加卸载会使得应力应变曲线出现塑性滞回环，且随着循环次数的增加，塑性滞回环逐渐靠右倾倒。?接下来，为研究
循环加卸载次数与耗散能之间的关系，需要大致计算每个塑性滞回环的面积。
三、塑性滞回环面积的计算
3.1计算思路
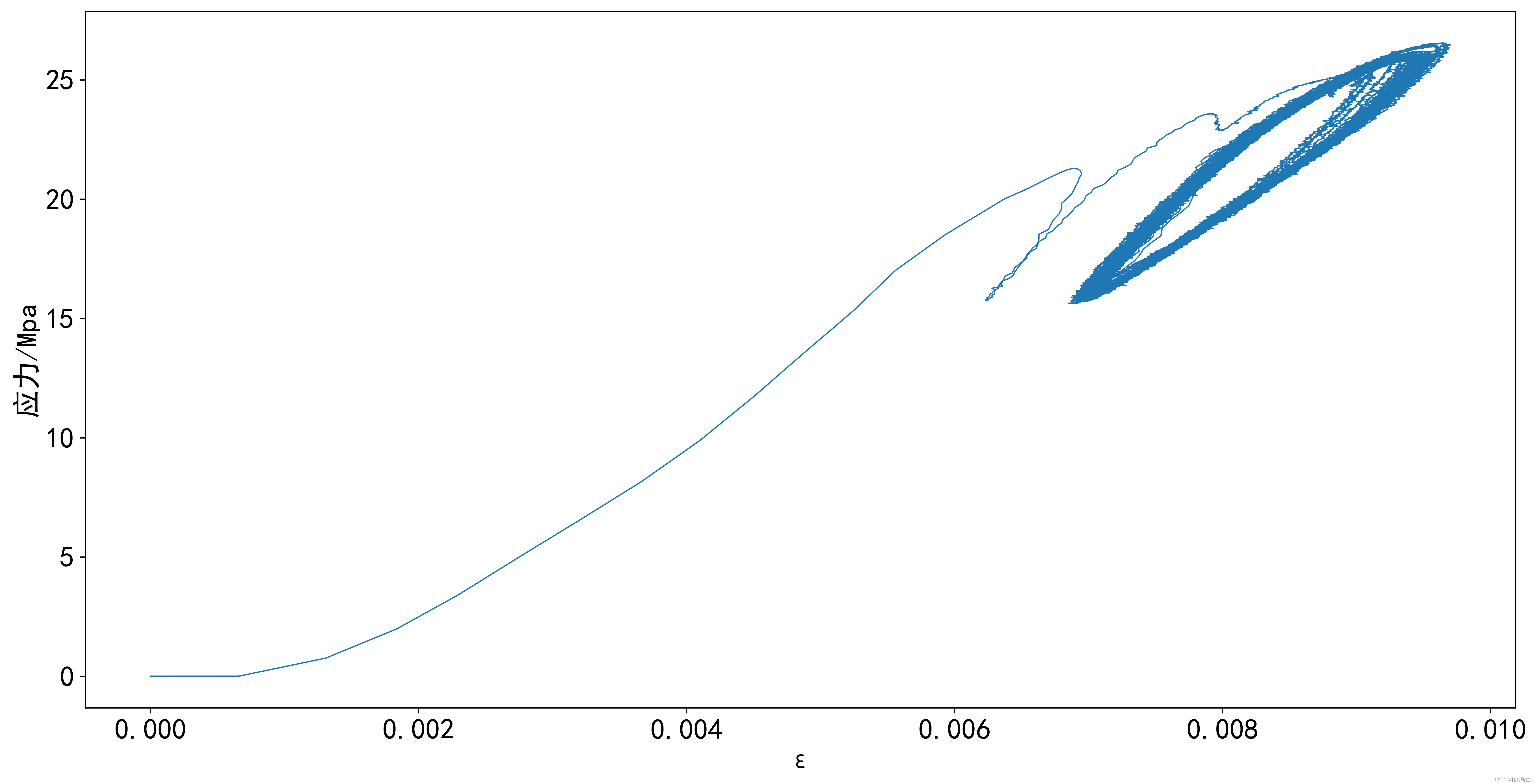
①从下图可以看出，要计算塑性滞回环的面积，关键是要确定塑性滞回环的高点和低点，即图中两个红色标记处（该种算法存在一定误差，即高点或低点变化并非如此尖锐）。
?②当确定好高点与低点后，可以采用定积分定义对该滞回环面积进行求解。主要思想即为将该区域在x轴上分为无限个矩形，利用各曲面的左或者右端点对应的函数值最为矩形的高，而每个区间的宽度最为矩形的底，于是利用一系列矩形面积的累加逼近该滞回环面积。具体内容可以参考定积分定义。
3.2塑性滞回环局部图
为观察单个塑性滞回环图形，使用如下代码读取相关CSV文件，并截取其中第10000条至11550个数据点，绘制相应应力应变曲线。
test = pd.read_csv(r"C:\Users\zsllsz2022\Desktop\testD8.csv",header=None,names=["应变","应力"])[10000:11550]
plt.figure(figsize=(16,8))
plt.plot(test["应变"],test["应力"],linewidth=0.8)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.xlabel("ε",fontsize=18)
plt.ylabel("应力/Mpa",fontsize=18)
plt.savefig("应力应变曲线-微观.jpg",dpi=500,bbox_inches = 'tight')
?从该图可以看出，局部塑性滞回环的应力应变曲线抖动明显，根据定积分定义可知，抖动的存在不利于面积的计算，即抖动部分的存在会抵消部分面积。因此，有必要对原始11W条数据进行采样，以消除局部细节上的抖动，得到较为整体的趋势。
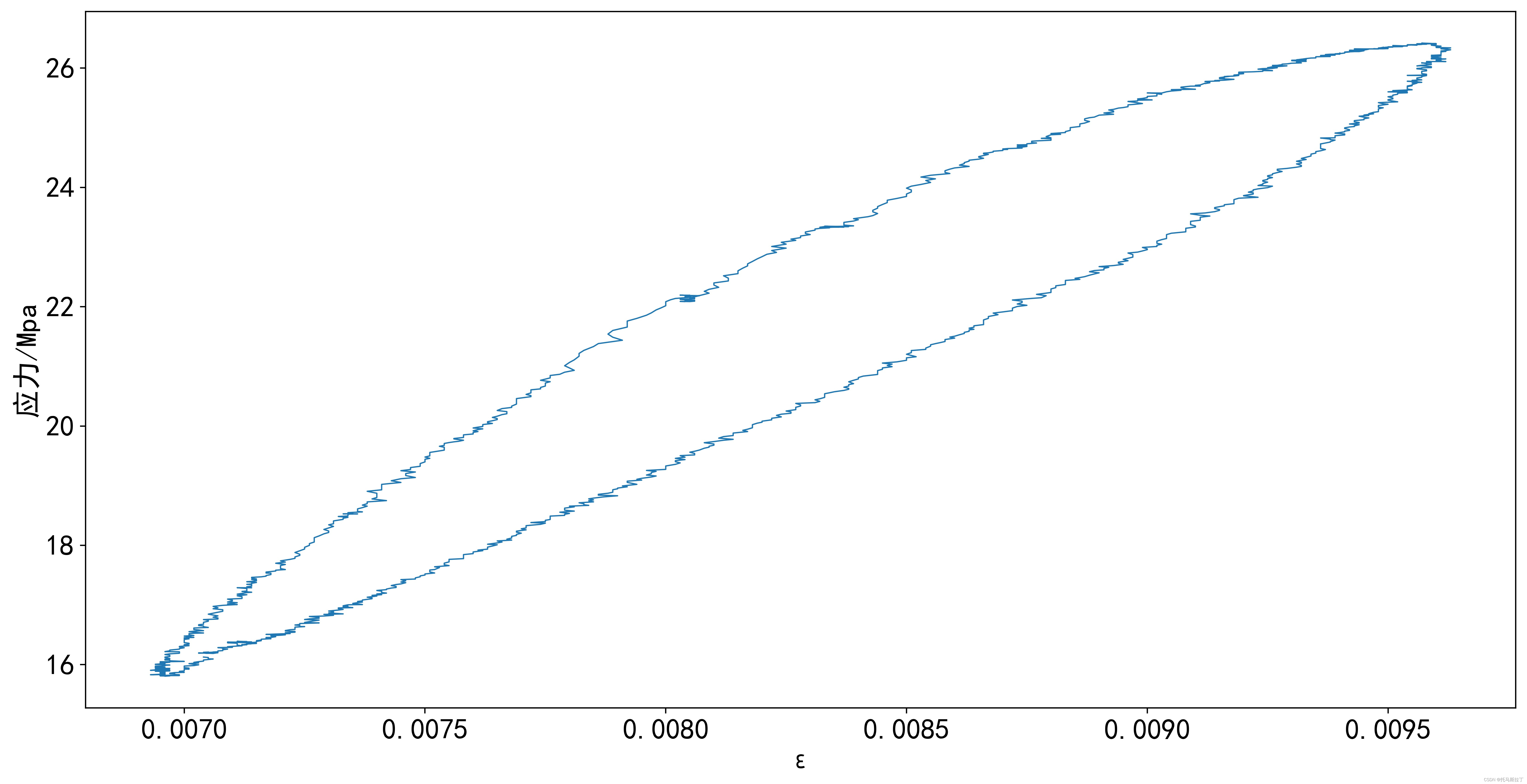
?于是，采用如下代码重新绘制局部塑性滞回环。从该代码可以看出，对原始数据进行采样，间隔为20，并重新绘制局部塑性滞回环。
test = pd.read_csv(r"C:\Users\zsllsz2022\Desktop\testD8.csv",header=None,names=["应变","应力"])[::20]
test = test[500:580]
plt.figure(figsize=(16,8))
plt.plot(test["应变"],test["应力"],linewidth=0.8)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.xlabel("ε",fontsize=18)
plt.ylabel("应力/Mpa",fontsize=18)
plt.savefig("应力应变曲线-微观-去抖动.jpg",dpi=500,bbox_inches = 'tight')
从去抖动后的应力应变曲线可以看出，塑性滞回环更为清晰，更加有利于塑性滞回环高点与低点的确定。
3.3塑性滞回环高点与低点的确定
相关代码如下。主要思路为对各数据点设置两个标志Flag并初始化为False。从低点到高点的过程中（即围成区域的上曲线），由于应力值的不断增加，因此flag1仍未False；而对于高点后一个数据而言，其应力值小于高点对应的应力值，此时会将flag1置为True，且对于高点到低点的过程中（即围成区域的下曲线），由于数值的不断降低，flag1均被置为True。于是，对于任一塑性滞回环而言，上曲线的flag1均为false，下曲线的flag1均为true。
于是，由上述结论可知，当flag1由false转为true时为高点，当flag1由true转为false时为低点，于是采用异或运算符进行判别，当不同flag1的情况出现时，根据异或的规则可将flag2置为true，于是一些列flag2为ture的点即为相应的高点与低点。
data = pd.read_csv(r"C:\Users\zsllsz2022\Desktop\testD8.csv",header=None,names=["应变","应力"])[::20]
data["flag1"] = False
data["flag2"] = False
temp = 0
for eachIndex in data[1:].index:
if data.loc[eachIndex]["应力"] < temp:
data.loc[eachIndex,"flag1"] = True
temp = data.loc[eachIndex]["应力"]
temp = False
for eachIndex in data[1:].index:
if data.loc[eachIndex]["flag1"] ^ temp:
data.loc[eachIndex,"flag2"] = True
temp = data.loc[eachIndex]["flag1"]
indexGet = data[data["flag2"]].index3.4面积计算
采用定积分的定义对面积进行计算，代码如下
areaDown = []
sum = 0
for start,end in zip(indexGet[::2],indexGet[1::2]):
# print(start,end)
# print(data.loc[start:end])
x = data.loc[start:end]["应变"].to_list()
y = data.loc[start:end]["应力"].to_list()
for index in range(1,len(x)):
sum += (x[index-1]-x[index])*y[index]
areaDown.append(sum)
# sum = 0
areaUp = []
sum = 0
indexGet = data[data["flag2"]].index.insert(0,0)
for start,end in zip(indexGet[::2],indexGet[1::2]):
# print(start,end)
x = data.loc[start:end]["应变"].to_list()
y = data.loc[start:end]["应力"].to_list()
for index in range(1,len(x)):
sum += (x[index]-x[index-1])*y[index]
areaUp.append(sum)
up = np.array(areaUp)
down = np.array(areaDown)
area = up-down四、煤岩能量耗散曲线
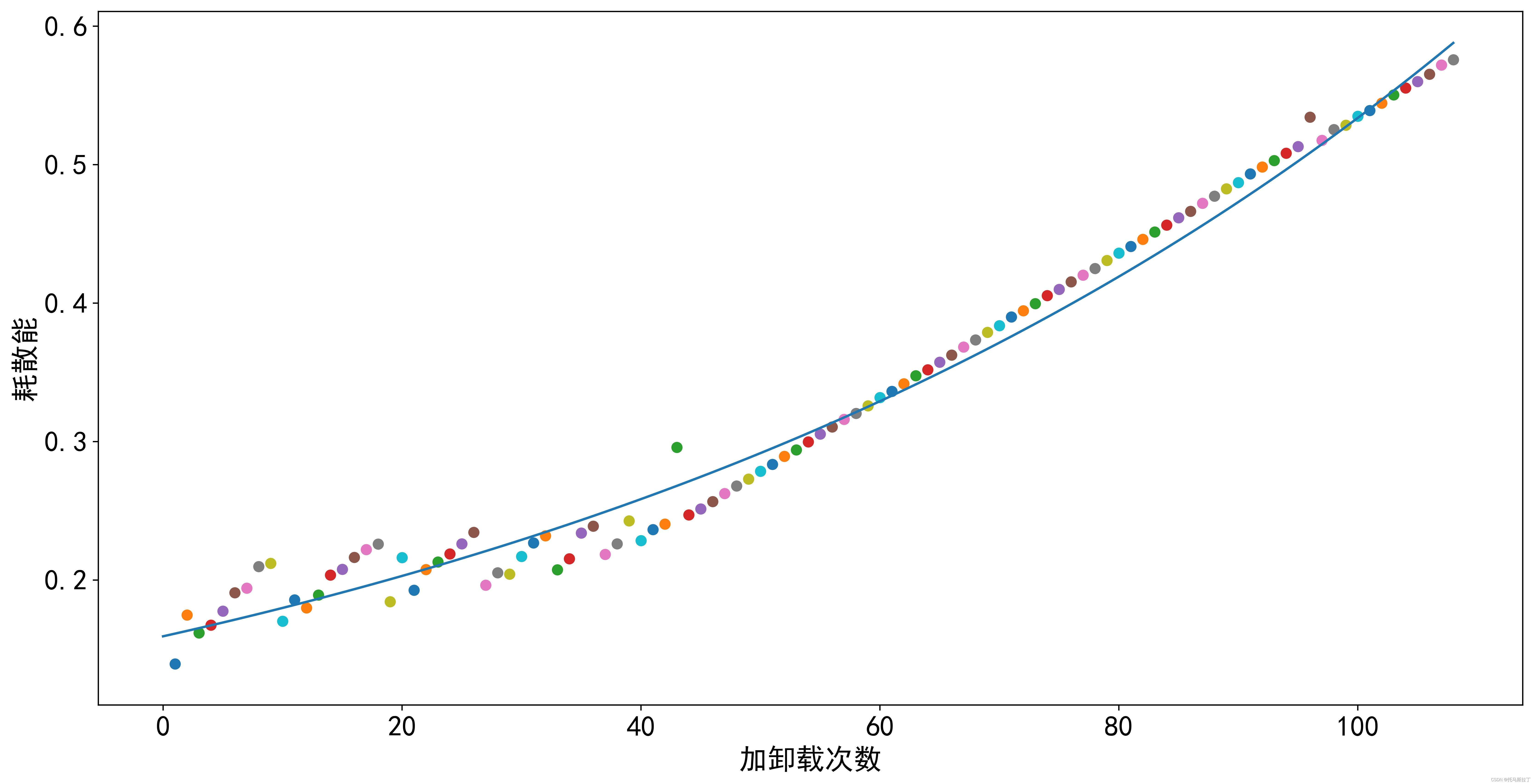
根据上述代码计算后可以得到各循环加载时的塑性滞回环面积或面积累加值，于是可以绘制相应的能量耗散曲线。
plt.figure(figsize=(16,8))
for index,y in enumerate(area):
plt.scatter(index+1,y)
# print(y)
a = 0.159377809961695
b = 0.0120870130063847
Y=a*np.exp(b*X)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.xlabel("加卸载次数",fontsize=18)
plt.ylabel("耗散能",fontsize=18)
plt.plot(X,Y)
plt.savefig("耗散能.jpg",dpi=500,bbox_inches = 'tight')
五、完整代码
import pandas as pd
import numpy as np
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm
from pylab import *
from numpy import *
import matplotlib.pyplot as plt
import pandas as pd
import math
import numpy as np
import copy
plt.rcParams['axes.unicode_minus']=False #用于解决不能显示负号的问题
mpl.rcParams['font.sans-serif'] = ['SimHei']
data = pd.read_csv(r"C:\Users\zsllsz2022\Desktop\testD8.csv",header=None,names=["应变","应力"])[::20]
data["flag1"] = False
data["flag2"] = False
temp = 0
for eachIndex in data[1:].index:
if data.loc[eachIndex]["应力"] < temp:
data.loc[eachIndex,"flag1"] = True
temp = data.loc[eachIndex]["应力"]
temp = False
for eachIndex in data[1:].index:
if data.loc[eachIndex]["flag1"] ^ temp:
data.loc[eachIndex,"flag2"] = True
temp = data.loc[eachIndex]["flag1"]
indexGet = data[data["flag2"]].index
areaDown = []
sum = 0
for start,end in zip(indexGet[::2],indexGet[1::2]):
# print(start,end)
# print(data.loc[start:end])
x = data.loc[start:end]["应变"].to_list()
y = data.loc[start:end]["应力"].to_list()
for index in range(1,len(x)):
sum += (x[index-1]-x[index])*y[index]
areaDown.append(sum)
# sum = 0
areaUp = []
sum = 0
indexGet = data[data["flag2"]].index.insert(0,0)
for start,end in zip(indexGet[::2],indexGet[1::2]):
# print(start,end)
x = data.loc[start:end]["应变"].to_list()
y = data.loc[start:end]["应力"].to_list()
for index in range(1,len(x)):
sum += (x[index]-x[index-1])*y[index]
areaUp.append(sum)
# sum = 0
up = np.array(areaUp)
down = np.array(areaDown)
area = up-down
plt.figure(figsize=(16,8))
for index,y in enumerate(area):
plt.scatter(index+1,y)
# print(y)
a = 0.159377809961695
b = 0.0120870130063847
Y=a*np.exp(b*X)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.xlabel("加卸载次数",fontsize=18)
plt.ylabel("耗散能",fontsize=18)
plt.plot(X,Y)
plt.savefig("耗散能.jpg",dpi=500,bbox_inches = 'tight')