[Python知识库]RSA p+1或p-1光滑

在rsa中，如果p或q生成不当导致p+1或者p-1光滑，则可能会易被攻击
参考：ctf wiki
?????????【大数分解】Pollard‘s p-1 method
光滑数 (Smooth number)：指可以分解为小素数乘积的正整数

RSA p-1光滑

p-1光滑（Pollard‘s p-1 method）：

根据费马小定理(Fermat Theorem)，若p是素数，且p不整除a，则有：
$$a^{p?1}\equiv 1(modp)$$
B-Smooth数：如果一个整数的所有素因子都不大于B，我们称这个数为B-Smooth数

例：$12=2?2?3，所以12是3?Smooth数$

原理：

伪代码：

于是有以下算法：

from gmpy2 import *
a = 2
n = 2
while True:
    a = powmod(a, n, N)
    res = gcd(a-1, N)
    if res != 1 and res != N:
        q = N // res
        print("p=",res)
        print("q=",q)
        break
    n += 1

RSA p+1光滑

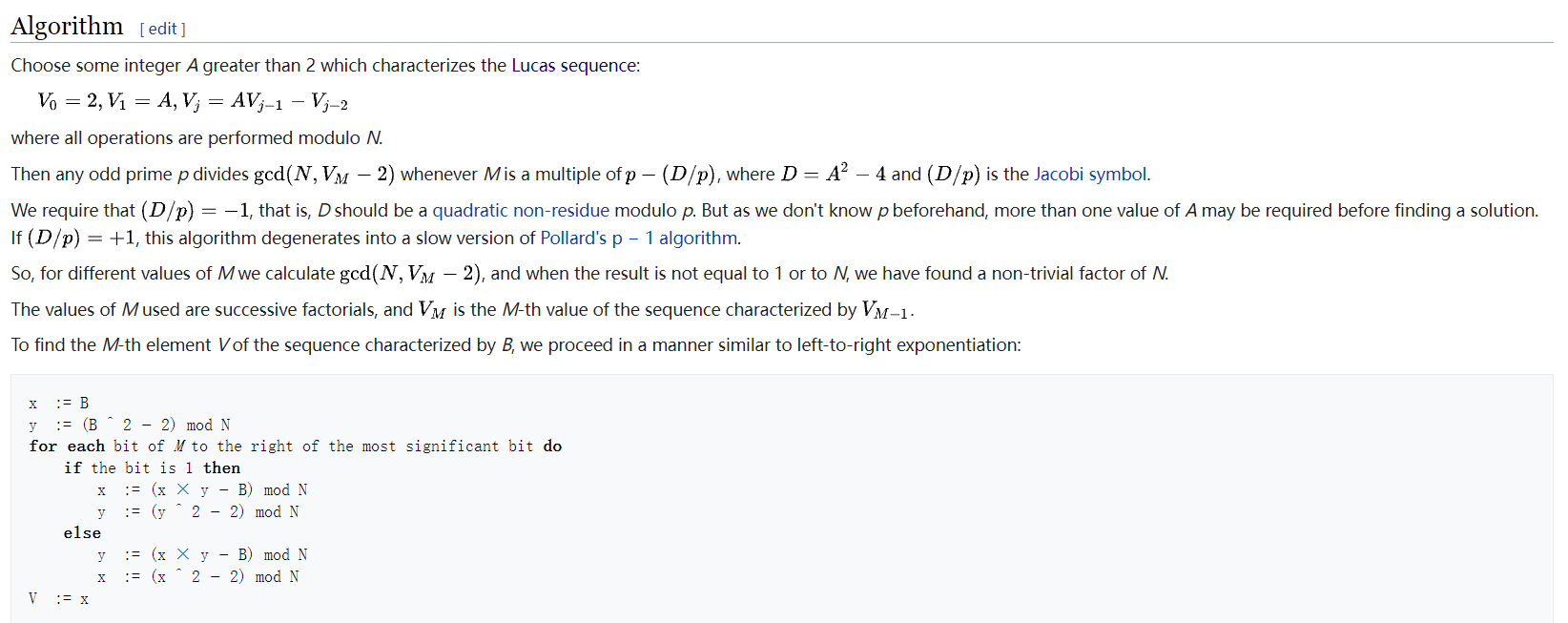
p+1光滑（Williams’s p + 1 algorithm）：
。。。原理如果有好奇的可以取wiki看一下，我们着重来实现算法：

def mlucas(v, a, n):
    """ Helper function for williams_pp1().  Multiplies along a Lucas sequence modulo n. """
    v1, v2 = v, (v**2 - 2) % n
    for bit in bin(a)[3:]: v1, v2 = ((v1**2 - 2) % n, (v1*v2 - v) % n) if bit == "0" else ((v1*v2 - v) % n, (v2**2 - 2) % n)
    return v1

for v in count(1):
    for p in primegen():
        e = ilog(isqrt(n), p)
        if e == 0: break
        for _ in xrange(e): v = mlucas(v, p, n)
        g = gcd(v-2, n)
        if 1 < g < n: return g # g|n
        if g == n: break

例题:

from random import choice
from Crypto.Util.number import isPrime, sieve_base as primes
from flag import flag


def myPrime(bits):
    while True:
        n = 2
        while n.bit_length() < bits:
            n *= choice(primes)
        if isPrime(n + 1):
            return n + 1

e = 0x10001
m = int.from_bytes(flag.encode(), 'big')
p = myPrime(2048)
q = getPrime(2048)
n = p * q
c = pow(m, e, n)

# n = 1224542620373200232525165378018470774334801515191193204875465445916504222883935188890019876845076388385357911730689547124547346252951158814249284724565588433721828377715469374541007756509231399263095022024229078845538543233785364809917406108015271780070196140628158427541531563472532516237632553353655535922926443707617182025475004547531104052989085765070550150028833424395972178427807901747932614235844448614858629761183210600428438018388051958214596857405813088470933109693499438012040822262549119751099008671892966082341548512112435591881692782766559736840448702039918465573051130405935280702181505538733234675792472428666968900055706926735800561218167237812066851519973807203332801575980055838563085817664973968944323258406789203078387708964307931318918136664885818917720073433998810127482159223895026085726623747340692196977140382318293090736558135980651252533606603312148824142669800602887109353065489282386215179238458743567166284295855288783740314247952124965482197632971993708775190564519250754150756867653033527903848903210074426177258586450311109023467944412194124015505951966140443860862968311560843608415723549525497729679097936310538451467530605937684408079363677707513923579164067808729408365886209340192468399685190639
# c = 145742860621666495489510776707734134231023214235535481878205099324276369445463746101469487674333600296204530932386373415987357363515200117271393133347844479863240936801112306080456942844796779477817786176831015954410967693647534326733641573842953783193563678040093734579772976410574013857063137696465850300484753282472377882118892522844694078667622111244886303620349388556315704648609353412177123230438077637042880490566244740468503369707900343076369151796123461132932226563486870411965536062339169788331659119981901553536009275158600580698576110294775989992794065611215170351808698605911258789407992833170968332058255364527244293283228694886707241979238145252395651417561576433516407782575454294499521347378058366557950770592472271985004818847838711060048422015207674862177145761946560579360220239667890707135827136815780729363013864130107808776517514214310689477005999830284272130148939734935547341627208913181919190392205389452185597444280635342938046191904062547803917870268485346888653569349729643793041018550170090471310374856687407102762116819004790791936814214507908374380597027347007448114684844276041116955473180015221164545212550832233007714133699817366745648092776901013502840540012912660742166994968977400188176557657864

代码审计可知p-1光滑
exp:

from Crypto.Util.number import *
N = 1224542620373200232525165378018470774334801515191193204875465445916504222883935188890019876845076388385357911730689547124547346252951158814249284724565588433721828377715469374541007756509231399263095022024229078845538543233785364809917406108015271780070196140628158427541531563472532516237632553353655535922926443707617182025475004547531104052989085765070550150028833424395972178427807901747932614235844448614858629761183210600428438018388051958214596857405813088470933109693499438012040822262549119751099008671892966082341548512112435591881692782766559736840448702039918465573051130405935280702181505538733234675792472428666968900055706926735800561218167237812066851519973807203332801575980055838563085817664973968944323258406789203078387708964307931318918136664885818917720073433998810127482159223895026085726623747340692196977140382318293090736558135980651252533606603312148824142669800602887109353065489282386215179238458743567166284295855288783740314247952124965482197632971993708775190564519250754150756867653033527903848903210074426177258586450311109023467944412194124015505951966140443860862968311560843608415723549525497729679097936310538451467530605937684408079363677707513923579164067808729408365886209340192468399685190639
c = 145742860621666495489510776707734134231023214235535481878205099324276369445463746101469487674333600296204530932386373415987357363515200117271393133347844479863240936801112306080456942844796779477817786176831015954410967693647534326733641573842953783193563678040093734579772976410574013857063137696465850300484753282472377882118892522844694078667622111244886303620349388556315704648609353412177123230438077637042880490566244740468503369707900343076369151796123461132932226563486870411965536062339169788331659119981901553536009275158600580698576110294775989992794065611215170351808698605911258789407992833170968332058255364527244293283228694886707241979238145252395651417561576433516407782575454294499521347378058366557950770592472271985004818847838711060048422015207674862177145761946560579360220239667890707135827136815780729363013864130107808776517514214310689477005999830284272130148939734935547341627208913181919190392205389452185597444280635342938046191904062547803917870268485346888653569349729643793041018550170090471310374856687407102762116819004790791936814214507908374380597027347007448114684844276041116955473180015221164545212550832233007714133699817366745648092776901013502840540012912660742166994968977400188176557657864
e=0x10001
import gmpy2
a = 2
n = 2
while True:
    a = pow(a, n, N)
    res = gmpy2.gcd(a-1, N)
    if res != 1 and res != N:
        q = N // res
        print("n=",n)
        print("p=",res)
        print("q=",q)
        break
    n += 1

d=gmpy2.invert(e,(res-1)*(q-1))
m=pow(c,d,N)
print(long_to_bytes(m))

可能会有人推荐primefac库，但经过少量实践初步验证，如果已知p-1或者p+1是光滑数，还是套用上面给的算法更好。有的时候p-1可能因子太多而形成指数爆炸，primefac针对这一点处理的不够好。
为了方便，可以讲primefac库内的源码修改为我们的代码。