1: 比较常用绘图函数介绍
1.1: 填充图
半透明填充图:设置faceAlpha属性为0-1的数值即可调整透明度:
%?生成三组x,y数据
x=linspace(-8,12,100);
y1=normpdf(x,4,6);
y2=normpdf(x,0,1).*0.5+normpdf(x,4,2).*0.5;
y3=normpdf(x,-3,2);
%?绘图
area(x,y1,'FaceAlpha',0.5);
hold?on
area(x,y2,'FaceAlpha',0.5);
area(x,y3,'FaceAlpha',0.5);

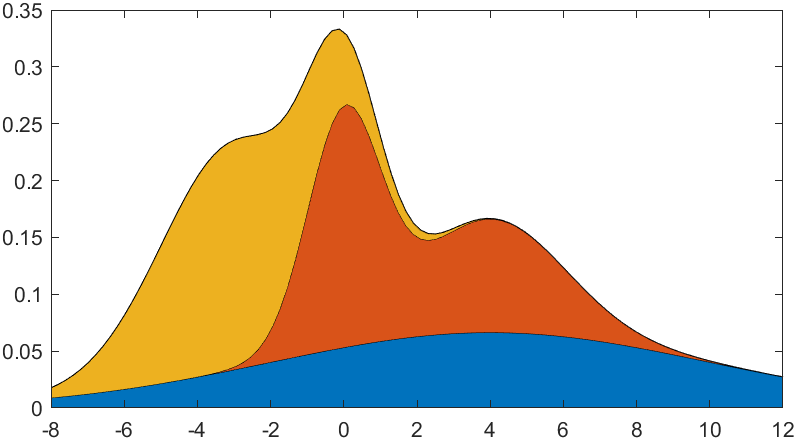
堆叠填充图:将y值变为列向量,横向拼接在一起,(想要调整层次关系只需要调整y向量的顺序即可):
%?生成三组x,y数据
x=linspace(-8,12,100);
y1=normpdf(x,4,6);
y2=normpdf(x,0,1).*0.5+normpdf(x,4,2).*0.5;
y3=normpdf(x,-3,2);
%?将y值变为列向量,横向拼接在一起
area(x,[y1',y2',y3'])
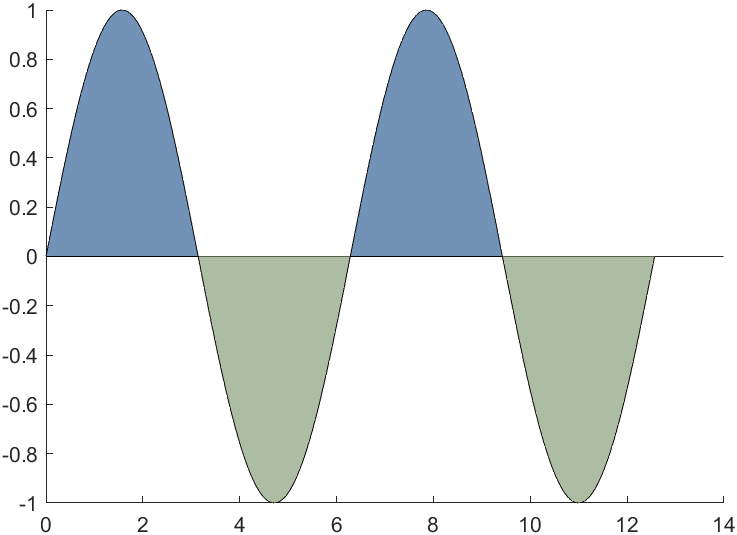
正负部分不同颜色:没想到啥更好的办法,分开画吧,(当然可以设置FaceColor设置更多样的颜色):
%?生成三组x,y数据
x=0:pi/100:4*pi;
y=sin(x);
y1=y;y1(y1<0)=0;
y2=y;y2(y2>0)=0;
hold?on
area(x,y1,'FaceColor',[114,146,184]./255);
area(x,y2,'FaceColor',[173,189,163]./255);
1.2: 双 y 轴图
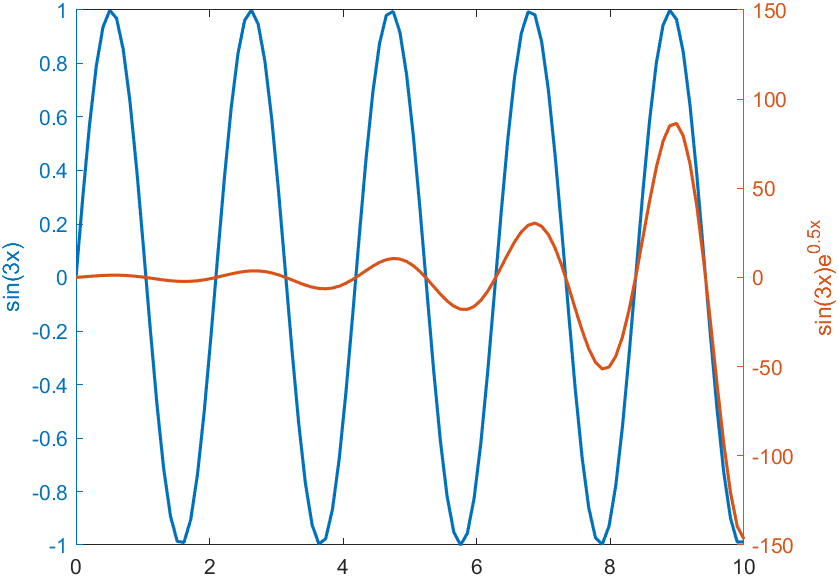
使用yyaxis函数即可,这里直接用一下官网的例子:
x=linspace(0,10);
y=sin(3*x);
yyaxis?left
plot(x,y,'LineWidth',1.5)
ylabel('sin(3x)')
z=sin(3*x).*exp(0.5*x);
yyaxis?right
plot(x,z,'LineWidth',1.5)
ylim([-150?150])
ylabel('sin(3x)e^{0.5x}')
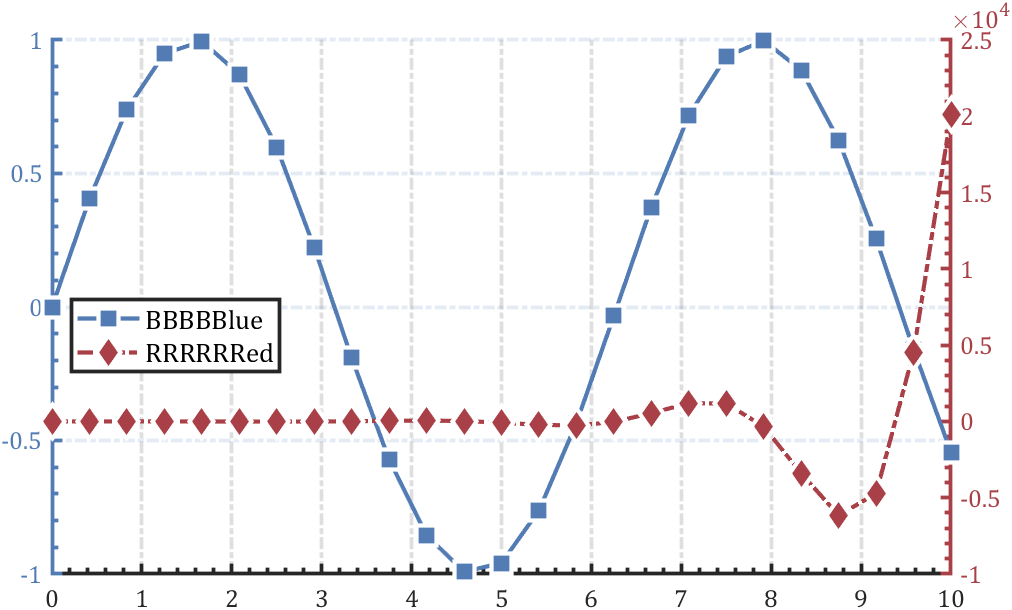
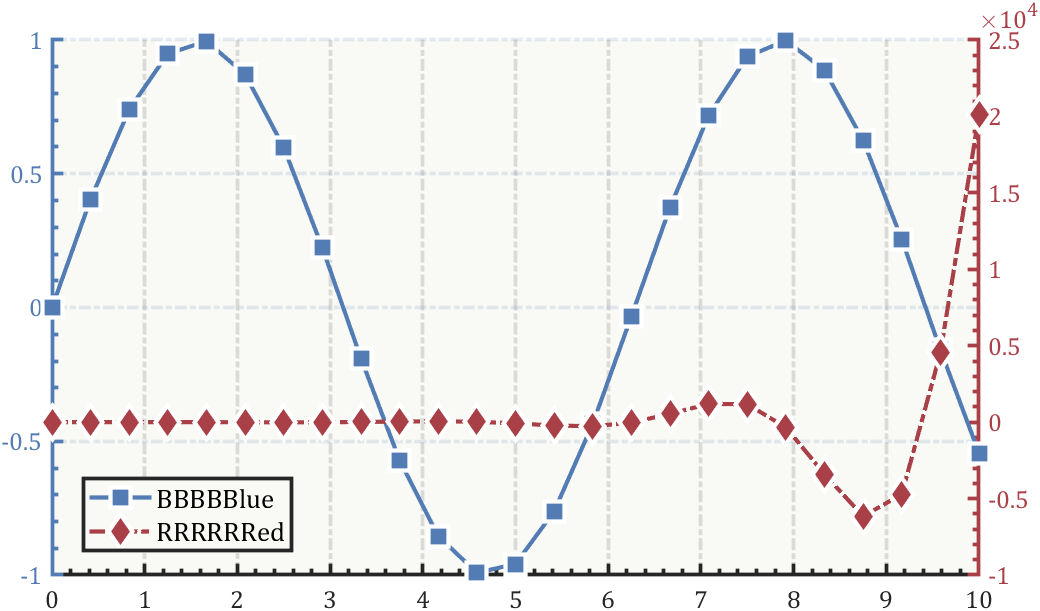
从 R2019b 开始,可以使用?colororder?函数设置色序,坐标区的每侧指定颜色方案,给个模板:
x=linspace(0,10,25);
y1=sin(x);
y2=sin(2*x).*exp(x);
%?设置轴颜色
%?以下方式均可:
%?colororder([1,1,0;0,0,1])
%?colororder({'b','m'})
colororder([82,124,179;169,64,71]./255)
%?左轴绘图
yyaxis?left
plot(x,y1,'s-','Color',[82,124,179]./255,'MarkerFaceColor',[82,124,179]./255,...
????'MarkerEdgeColor',[1,1,1],'LineWidth',2,'MarkerSize',12)??
%?坐标区域修饰(部分)
ax=gca;
%?加上调整背景颜色这句就是下图
%?ax.Color=[249,250,245]./255;
ax.LineWidth=1.8;
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.GridLineStyle='-.';
ax.FontName='Cambria';
ax.FontSize=12;?
%?右轴绘图
yyaxis?right
plot(x,y2,'d-.','Color',[169,64,71]./255,'MarkerFaceColor',[169,64,71]./255,...
????'MarkerEdgeColor',[1,1,1],'LineWidth',2,'MarkerSize',12)??
%?坐标区域修饰(部分)
ax=gca;grid?on;box?off
ax.YMinorTick='on';
%?增添图例
lgd=legend('BBBBBlue','RRRRRRed');
lgd.Location='best';
lgd.FontSize=13;
1.3: 曲线拟合相关
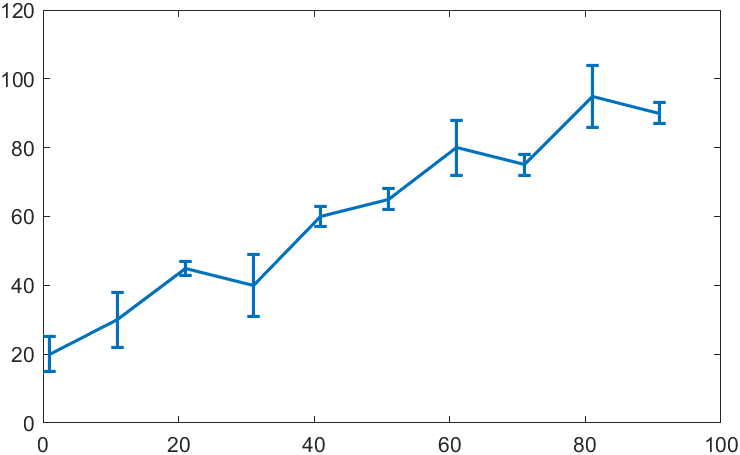
带误差条的线图:
x=1:10:100;
y=[20?30?45?40?60?65?80?75?95?90];?
err=[5?8?2?9?3?3?8?3?9?3];
errorbar(x,y,err,'LineWidth',1.5)
拟合曲线后绘制绘制带置信区间图像:
x=-3:.25:5;?
y=-0.3*x+3.5.*x.^2-x.^3+20*rand([1,length(x)]);?
[p,S]=polyfit(x,y,3);?
%?计算以p为系数的多项式在 x 中各点处的拟合值。将误差估计结构体指定为第三个输入,
%?以便polyval 计算标准误差的估计值。标准误差估计值在 delta 中返回。
[y_fit,delta]=polyval(p,x,S);
%?绘制原始数据、线性拟合和 95%?预测区间 y±2Δ。
uy=y_fit+2*delta;
dy=y_fit-2*delta;
%?绘制原始数据
plot(x,y,'rx','LineWidth',1.2)
hold?on
%?绘制拟合曲线
plot(x,y_fit,'Color',[82,124,179]./255,'LineWidth',1.5)
%?绘制置信区间
plot([x',x'],[uy',dy'],'Color',[82,124,179]./255,'LineWidth',1.2,'LineStyle','--')
fill([x,x(end:-1:1)],[uy,dy(end:-1:1)],[82,124,179]./255,'EdgeColor','none','FaceAlpha',.2)
title('Linear?Fit?of?Data?with?95%?Prediction?Interval')
legend('Data','Linear?Fit','95%?Prediction?Interval')?

2: 抽象多元复合函数偏导数
举个例子:
syms?f1(x,y)?f2(x,y)?F(x,y)
dFdx=diff(F(f1,f2),x)
求解结果:
dFdx = D([1], F)(f1(x, y), f2(x, y))*diff(f1(x, y), x) + D([2], F)(f1(x, y), f2(x, y))*diff(f2(x, y), x)
不太美观,pretty一下:
pretty(dFdx)
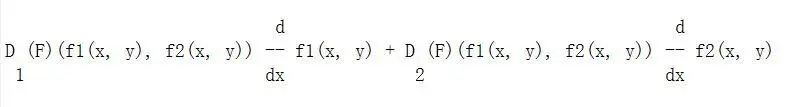
3: 含符号函数的数组的索引
这是对于知乎上一个问题的回答,原问题遇到的情况图片如下(即数组的某行某列的元素无法直接获取):
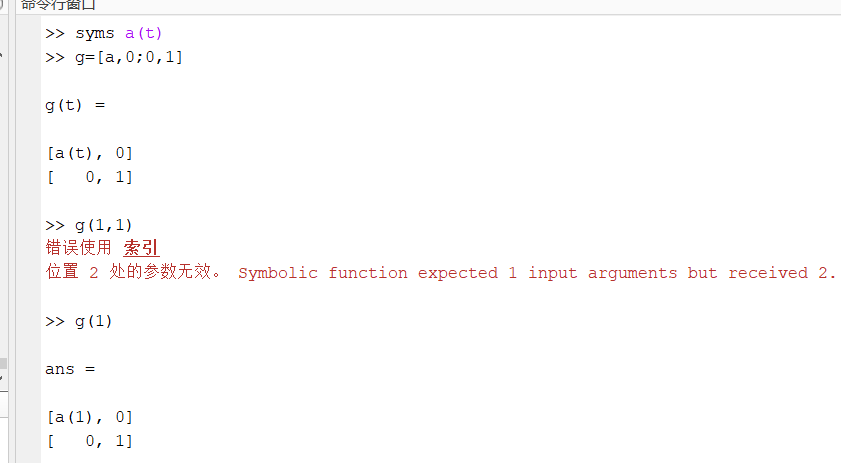
可以使用formula函数获取每个位置的对象,给个实例:
syms?a(t)
g=[a,0;0,1];
gb=formula(g);
gb(1,1)
ans = a(t)
4: fplot绘图取消渐近线
就举tan(x)的例子,正常fplot函数绘图效果:
fplot(@tan,[-3,3],'LineWidth',1.5)

ShowPoles属性设置为'off'就可以关闭辅助渐近线:
fplot(@tan,[-3,3],'LineWidth',1.5,'ShowPoles','off')

5: 特殊稀疏矩阵创建
之后可能会专门出一期特殊矩阵创建的合集,本期的问题是:构造一个100阶的稀疏矩阵A,要求非零元素有50个,且为1到50
%?10000个数里随机选不重复的50个数
pos=randperm(10000,50);
%?将线性索引转换为下标
[row,col]=ind2sub([100,100],pos);
%?稀疏矩阵创建
A=sparse(row,col,1:50)
运算结果(展示部分):
(96,2) 6
(48,6) 50
(96,9) 42
... ...
6: MATLAB 有趣应用
来自CSDN的小问题:3对情侣参加婚礼,3个新郎为ABC,3个新娘为XYZ,有人想知道究竟谁与谁结婚,于是问其中中的三位,得到如下结果:A说他将和X结婚;X说她的未婚夫是C;C说他将和Z结婚,事后知道这几个人都在开玩笑说的都是假的,那么用程序实现究竟谁与谁结婚;
groom={'A','B','C'};
bride={'X','Y','Z'};
?
condition=perms([1,2,3]);%?用数字来表示新娘
?
condition(condition(:,1)==1,:)=[];?%A和X的删掉
condition(condition(:,3)==1,:)=[];?%C和X的删掉
condition(condition(:,3)==3,:)=[];?%C和Z的删掉
?
%?输出结果
for?i=1:3
????disp([groom{i},'--',bride{condition(i)}])?
end
A--Z
B--X
C--Y
7: 转置与共轭转置
对于实矩阵而言'和.'没有任何区别,但是对于符号矩阵和虚数矩阵就不一样了,前者是共轭转置,后者才是转置:
A=[0,3+4i;0,0];
A1=A'
A2=A.'
A1 =
0.0000 + 0.0000i ? 0.0000 + 0.0000i
3.0000 - 4.0000i ? 0.0000 + 0.0000i
A1 =
0.0000 + 0.0000i ? 0.0000 + 0.0000i
3.0000 + 4.0000i ? 0.0000 + 0.0000i
7: 转数组中的 end
end在数组中不仅仅有代替最后,实际上也重载了每个维度的最大尺度,举个例子,以下的写法在MATLAB中都是可行的实际上:
A=1:10;
b1=A(end:-1:1)
b2=A(end-2)
b3=A(end/2+1)
b1 =?
10 ? ? 9 ? ? 8 ? ? 7 ? ? 6 ? ? 5 ? ? 4 ? ? 3 ? ? 2 ? ? 1
b2 = 8
b3 = 6