写在前面
? ? ? ? 光路是很重要的,用mma可以很好得模拟它.但是很遗憾,mma跑得不快,如果是因为sanction而用不上正版的话...
? ? ? ? 嗯,所以会python是很重要的
? ? ? ? 如果有能力自己去解一个方程的话,也可以...
? ? ? ? 但是题主选用了Scipy??
? ? ? ? 至于可视化吗,题主选用了matplotlib
? ? ? ? 有些地方为了算的快一点,也用了multiprocessing? 和 numpy
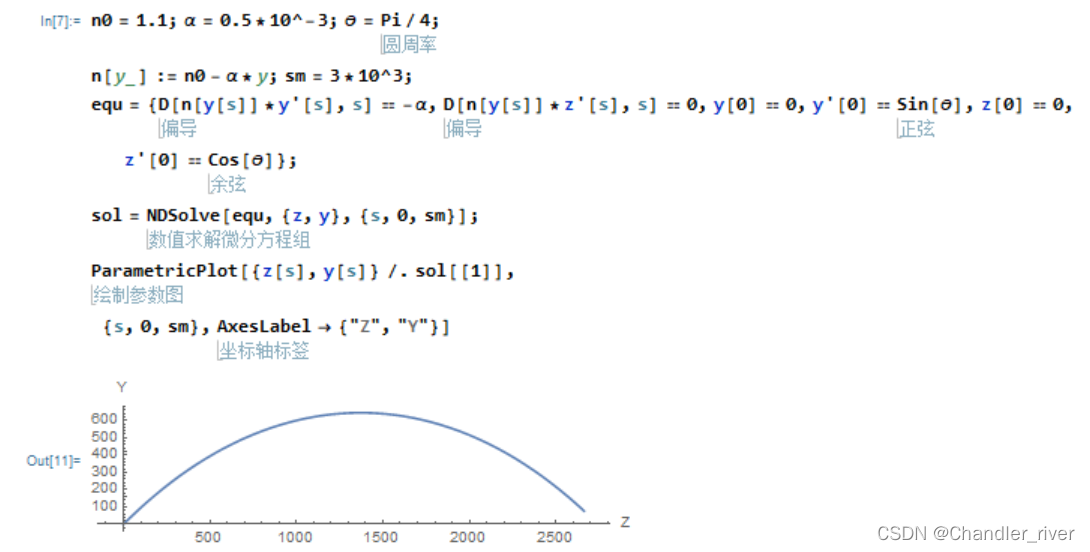
几何光学:在连续折射率介质中进行光线追踪
- 光线方程
- 模拟光在大气中的折射
- 模拟光在光纤中的传播
- 纤芯的折射率模型
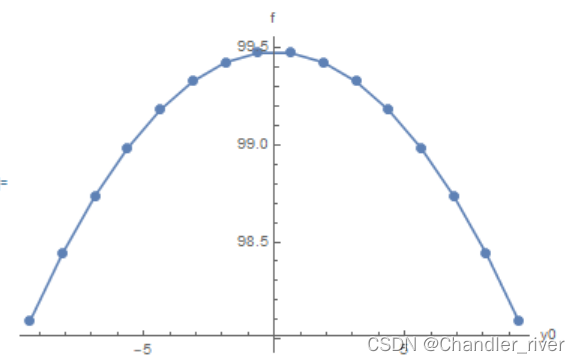
- 纤芯中心折射率n1? 包层区域折射率n2
- 对于单模光纤? n2/n1? 通常在99.4%~99.7%
- 对于多模光纤? n2/n1? 通常在98%~99%
- 光线围绕纤芯中心周期性地向前传播,表现出自聚焦的特性
- 光线路径的周期大小与初始入射角有关,不同的光线将不严格聚集在相同的点上,一个入射的光脉冲将逐渐弥漫散开
- 纤芯的折射率模型
- 模拟光在大气中的折射
几何光学:在折射率跃变介质中进行光线追踪
- Snell 定律
- 球面凸透镜
- 球面方程
- 透镜半径
- 曲面的法线方向
- 平行光束正入射
- 光束的粗细相对于凸透镜半径r来说? y方向上宽度为 -0.1r~0.1r


- 平行光斜入射
- 轴上光源
-
轴外光源
-
-
凸透镜的近轴焦点
-
-
厚透镜的形式焦距的倒数
-
-
物点经过凸透镜之后的像距
-
待写
-
- 球面方程
- 三棱镜
-
?白光的色散和色光的合成
-
单个三棱镜的色散
-
两个三棱镜的色散??
-
- 消色差透镜(凹凸组合透镜)
波动光学:光衍射的计算
- 根据夫琅禾费衍射理论,衍射场的振幅分布为:
衍射屏的透射函数
- 衍射强度的分布
- 单个圆孔的衍射

- 硬核的来了,这个程序等他跑完也就该下班了,几个小时也不一定跑的完,我们还是换Python取编写.当然,如果读者会C或者Fortran啥的那更好的,不过,写个几百行累死人了,不是吗?

- 热力图是表征强度的一个很好的工具,
- 下面给出单个圆孔的夫琅禾费衍射计算程序(以方向角形式展示的,所以他不是一个标砖的圆,这个演示完会有用X,Y坐标表示的程序)
- 当然,以Python语言的一般特性,这个n取到100的时候,,,,
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.integrate import dblquad
import math
#lambda 用k表示
r = 3.0
k = 0.6
q = 2*math.pi / k
#alpha 用a表示 beta用b表示
a0 = math.pi
b0 = math.pi
n = 10
def fun(D,k):
a = D[0]
b = D[1]
u = "1"
x1 = 3
x2 = -3
y1 = lambda x: (9-x**2)**0.5
y2 = lambda x: -(9-x**2)**0.5
U1 = dblquad(lambda x,y:eval(u)*math.cos(2*math.pi*(x*math.sin(a)+y*math.sin(b))/k)
,x1,x2,y1,y2)
U2 = dblquad(lambda x,y:eval(u)*math.sin(2*math.pi*(x*math.sin(a)+y*math.sin(b))/k)
,x1,x2,y1,y2)
U = U1[0]**2 + U2[0]**2
return U
data0 = np.array([[[i,j] for j in np.linspace(-a0,a0,n)] for i in np.linspace(-b0,b0,n)])
data = [[fun(j,k) for j in i] for i in data0]
#注意!
data = np.array(data)#设置二维矩阵
f,ax = plt.subplots(figsize=(11,12))
#数据
f = open("diffraction.txt","w")
f.write(str(data))
f.close()
#注意!
sns.heatmap(data, ax=ax,vmin=0,vmax=6,cmap='YlOrRd',linewidths=2,cbar=True)
#热力图绘制代码
plt.title('heatmap')
plt.ylabel('y_label')
plt.xlabel('x_label')
plt.savefig("diffraction.jpg")
plt.show()
- 这时候必须multiprocessing辅助一下了
-
import matplotlib.pyplot as plt import numpy as np import seaborn as sns from scipy.integrate import dblquad import math import datetime import multiprocessing as mp import time a0 = math.pi/10 b0 = math.pi/10 n = 100 k = 0.6 def final_fun(name, param): result = [] global a0 global b0 global n global k A = np.linspace(-a0,a0,n) B = np.linspace(-b0,b0,n) for params in param: a = A[params[0]] b = B[params[1]] u = "1" x1 = 3 x2 = -3 y1 = lambda x: (9-x**2)**0.5 y2 = lambda x: -(9-x**2)**0.5 U1 = dblquad(lambda x,y:eval(u)*math.cos(2*math.pi*(x*math.sin(a)+y*math.sin(b))/k) ,x1,x2,y1,y2) U2 = dblquad(lambda x,y:eval(u)*math.sin(2*math.pi*(x*math.sin(a)+y*math.sin(b))/k) ,x1,x2,y1,y2) U = U1[0]**2 + U2[0]**2 result.append(U) return {name:result} if __name__ == '__main__': start_time = time.time() num_cores = int(mp.cpu_count()) pool = mp.Pool(num_cores) param_dict = {"task1":[[0,i] for i in range(n)], "task2":[[1,i] for i in range(n)], "task3":[[2,i] for i in range(n)], "task4":[[3,i] for i in range(n)], "task5":[[4,i] for i in range(n)], "task6":[[5,i] for i in range(n)], "task7":[[6,i] for i in range(n)], "task8":[[7,i] for i in range(n)], "task9":[[8,i] for i in range(n)], "task10":[[9,i] for i in range(n)], "task11":[[10,i] for i in range(n)], "task12":[[11,i] for i in range(n)], "task13":[[12,i] for i in range(n)], "task14":[[13,i] for i in range(n)], "task15":[[14,i] for i in range(n)], "task16":[[15,i] for i in range(n)], "task17":[[16,i] for i in range(n)], "task18":[[17,i] for i in range(n)], "task19":[[18,i] for i in range(n)], "task20":[[19,i] for i in range(n)], "task21":[[20,i] for i in range(n)], "task22":[[21,i] for i in range(n)], "task23":[[22,i] for i in range(n)], "task24":[[23,i] for i in range(n)], "task25":[[24,i] for i in range(n)], "task26":[[25,i] for i in range(n)], "task27":[[26,i] for i in range(n)], "task28":[[27,i] for i in range(n)], "task29":[[28,i] for i in range(n)], "task30":[[29,i] for i in range(n)], "task31":[[30,i] for i in range(n)], "task32":[[31,i] for i in range(n)], "task33":[[32,i] for i in range(n)], "task34":[[33,i] for i in range(n)], "task35":[[34,i] for i in range(n)], "task36":[[35,i] for i in range(n)], "task37":[[36,i] for i in range(n)], "task38":[[37,i] for i in range(n)], "task39":[[38,i] for i in range(n)], "task40":[[39,i] for i in range(n)], "task41":[[40,i] for i in range(n)], "task42":[[41,i] for i in range(n)], "task43":[[42,i] for i in range(n)], "task44":[[43,i] for i in range(n)], "task45":[[44,i] for i in range(n)], "task46":[[45,i] for i in range(n)], "task47":[[46,i] for i in range(n)], "task48":[[47,i] for i in range(n)], "task49":[[48,i] for i in range(n)], "task50":[[49,i] for i in range(n)], "task51":[[50,i] for i in range(n)], "task52":[[51,i] for i in range(n)], "task53":[[52,i] for i in range(n)], "task54":[[53,i] for i in range(n)], "task55":[[54,i] for i in range(n)], "task56":[[55,i] for i in range(n)], "task57":[[56,i] for i in range(n)], "task58":[[57,i] for i in range(n)], "task59":[[58,i] for i in range(n)], "task60":[[59,i] for i in range(n)], "task61":[[60,i] for i in range(n)], "task62":[[61,i] for i in range(n)], "task63":[[62,i] for i in range(n)], "task64":[[63,i] for i in range(n)], "task65":[[64,i] for i in range(n)], "task66":[[65,i] for i in range(n)], "task67":[[66,i] for i in range(n)], "task68":[[67,i] for i in range(n)], "task69":[[68,i] for i in range(n)], "task70":[[69,i] for i in range(n)], "task71":[[70,i] for i in range(n)], "task72":[[71,i] for i in range(n)], "task73":[[72,i] for i in range(n)], "task74":[[73,i] for i in range(n)], "task75":[[74,i] for i in range(n)], "task76":[[75,i] for i in range(n)], "task77":[[76,i] for i in range(n)], "task78":[[77,i] for i in range(n)], "task79":[[78,i] for i in range(n)], "task80":[[79,i] for i in range(n)], "task81":[[80,i] for i in range(n)], "task82":[[81,i] for i in range(n)], "task83":[[82,i] for i in range(n)], "task84":[[83,i] for i in range(n)], "task85":[[84,i] for i in range(n)], "task86":[[85,i] for i in range(n)], "task87":[[86,i] for i in range(n)], "task88":[[87,i] for i in range(n)], "task89":[[88,i] for i in range(n)], "task90":[[89,i] for i in range(n)], "task91":[[90,i] for i in range(n)], "task92":[[91,i] for i in range(n)], "task93":[[92,i] for i in range(n)], "task94":[[93,i] for i in range(n)], "task95":[[94,i] for i in range(n)], "task96":[[95,i] for i in range(n)], "task97":[[96,i] for i in range(n)], "task98":[[97,i] for i in range(n)], "task99":[[98,i] for i in range(n)], "task100":[[99,i] for i in range(n)]} results = [pool.apply_async(final_fun, args=(name, param)) for name, param in param_dict.items()] results = [p.get() for p in results] end_time = time.time() use_time = end_time - start_time print("多进程计算 共消耗: " + "{:.2f}".format(use_time) + " 秒") data = [i["task"+str(results.index(i)+1)] for i in results] data = np.array(data) f = open("diffraction.txt","w") f.write(str(data)) f.close() fig,ax = plt.subplots(figsize=(11,12)) sns.heatmap(data, ax=ax,vmin=0,vmax=6,cmap='YlOrRd',\ linewidths=2,cbar=True) plt.title('diffraction') plt.ylabel('y_label') plt.xlabel('x_label') plt.savefig("diffraction.jpg") plt.show()
用x,y坐标表示,这个更符合人的观察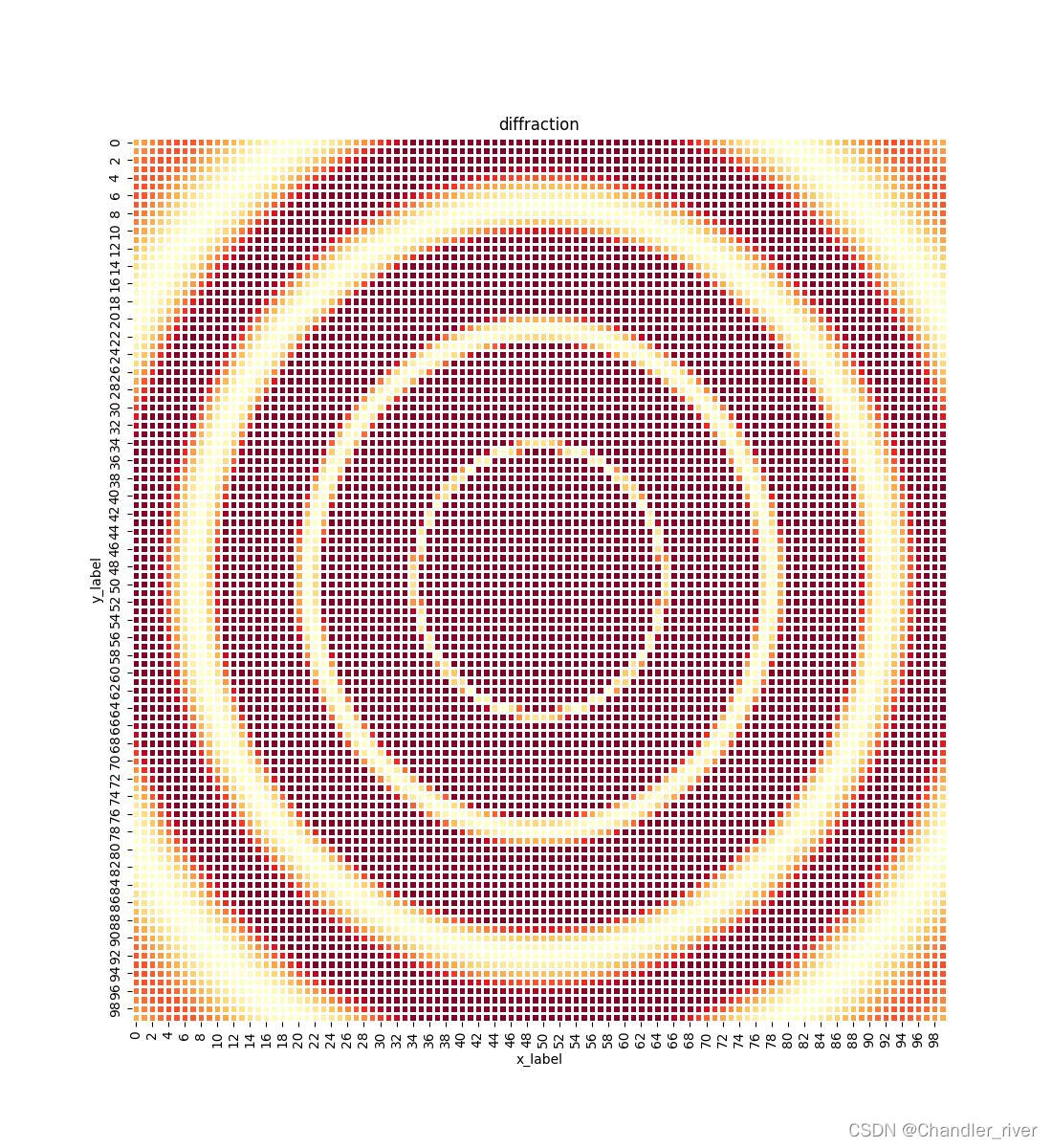
- 单个矩形孔衍射

?
- 随机孔衍射
? ? ??