前言

??第一节，我们学习【Python开发环境的搭建】，知道什么了是程序设计语言，了解了Python语言的发展及特点，并进行Python开发环境的搭建以及Python集成开发环境PyCharm的安装及模板设置。
??第二节，我们学习【Python语言的基本语法元素】。包括Python程序的格式框架（缩进、注释），语法元素名称，数据类型和语句元素以及基本的输入输出函数。
??本节，我们将学习【Python的基本数据类型】。数字类型：整数类型、浮点数类型、复数类型。字符串类型以及数据类型之间的转换。

Python基本数据类型

# 常见数据类型
"""
整型:int   98

浮点型:float   3.292992

布尔型:False  0;    True   1

字符串:str  'hello'    '你好'  "world"
"""

一、数字类型

Python中提供3种数字类型：整数类型、浮点数类型和复数类型。

1.整数类型

Python中的整数没有取值范围的限制，理论上来讲只要内存能够存储，Python可以使用任意大小的整数。

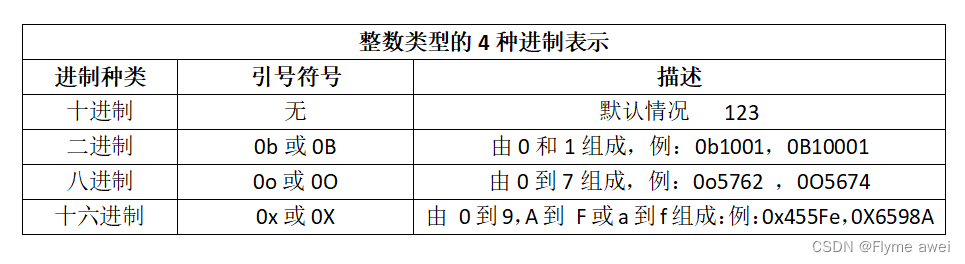
整数类型有4种进制表示方式：十进制、二进制、八进制、十六进制。默认情况下，采用十进制，如果需要表示其它进制方式需要增加引导符号。

??二进制是一套计数方法，每个位置上的数有 2 种可能（0 - 1）；二进制是计算机的执行语言，但是早在计算机出现前就存在这套计数方法，最早可追溯到古埃及。在日常生活中，我们使用的是十进制，每个位置上的数有 10 种可能（0 - 9）。
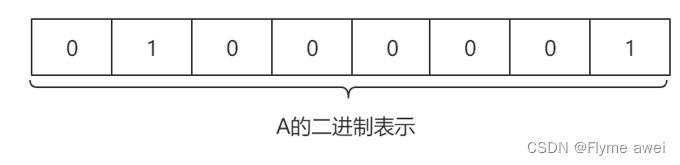
在这里插入图片描述

	8位(bit) = 1 字节(byte)
	1024字节（byte）= 1 千字节（KB）
	024千字节（KB）= 1 兆 （MB）
 	1024MB = 1GB

整数类型的4种进制表示
在这里插入图片描述

# -*- coding: utf-8 -*-
# @File  : demo.py
# @author: Flyme awei 
# @email : 1071505897@qq.com
# @Time  : 2022/8/3 23:28

"""
十进制 默认的进制
二进制 0b开头
八进制 0o开头
十六进制 0x开头
"""
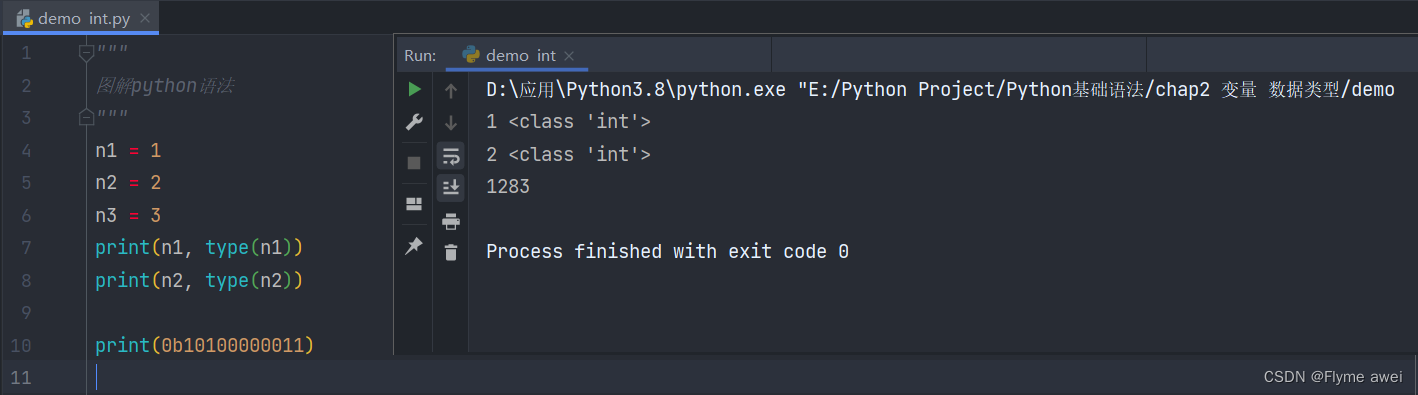
print('二进制，0b开头', 0b1010010)
print('八进制，0o开头', 0o7432647)
print('十六进制，0x开头', 0xA36540984)

不同进制的整数之间可以直接运算或比较，程序无论采用哪种进制表达数据，计算机内部都以相同的格式存储数值，进制之间的运算结果默认以十进制方式显示。
在这里插入图片描述

2.浮点数类型

浮点数表示带有小数的数值，在Python语言中的浮点数类型必须带有小数部分，小数部分可以是0。比如说98是整数，98.0就是浮点数。

浮点数有2种表示方法：十进制表示形式和科学计数法表示形式。浮点数没有其它进制表示形式。

科学计数法使用字母e或者E作为幂的符号，以10为基数。举例<a>e<b>表示a*10**b

比如说：1.01e3 表示1.01*103，就是1010.0，-1.01e-3表示-1.01*10-3，就是-0.00101。

# -*- coding: utf-8 -*-
# @File  : demo.py
# @author: Flyme awei 
# @email : 1071505897@qq.com
# @Time  : 2022/8/3 23:28

# 浮点型 float()
a = 3.114152
print(a, type(a))

# 计算机采用二进制存储，浮点数存储不精确
n1 = 1.1
n2 = 2.2
print(n1+n2)    # 3.300000000003

# 浮点数计算  导入decimal模块    decimal 十进制
from decimal import Decimal  # 直接导入decimal模块的Decimal方法
print(Decimal('1.1')+Decimal('2.2'))

import decimal  # 导入decimal模块
print(decimal.Decimal(1.1)+decimal.Decimal(2.2))  # .Decimal 调用decimal模块的Decimal方法

浮点数的取值范围和小数精度受不同计算机系统的限制。浮点数的取值范围[-10308,10308]，浮点数之间的区分精度约为2.22*10-16。对于绝大部分运算来说，浮点数类型的数值范围和小数精度足够“可靠”。一般认为浮点数类型没有范围限制。

>>> 1.01 + 2.02
3.0300000000000002
>>> 123455.346788*0978.456
120795624.79679933
>>> 98765.37854/3456.54677
28.573424608977593

相同数值的整数和浮点数哪那个运算精度更高呢？整数1010和浮点1010.0它们的值是相等的，但是在进行幂运算时结果却不同。

>>> pow(1010,32)
1374940678531097054162291350571104044956417832049380936096496320100000000000000000000000000000000
>>> pow(1010.0,32)
1.3749406785310972e+96
>>>

Python语言的浮点数运算存在一个“不确定尾数”问题，即两个浮点数运算时，有可能会增加一些“不确定”的尾数。

>>> 0.1 + 0.2
0.30000000000000004

??这不是计算机运行错误，而是正常情况，因为在计算机内部，使用二进制表示浮点数，受计算机表示浮点数使用的存储宽度限制，这个二进制数不完全等于0.1而是最接进0.1的二进制数。因此在计算机内部了进行计算时是将最接近0.1和最接近0.2的两个数进行加运算，因此产生的数接近0.3，但未必是最接近的，反映到十进制上就产生了这个尾数。这个尾数是多少，计算机内部会根据二进制运算确定产生。

不确定尾数问题会对浮点数运算结果的判断造成一定困扰。由于0.1+0.2的运算结果中存在不确定尾数，所以与0.3判断是否相等时结果为False。

>>> 0.1 + 0.2 == 0.3
False

在Python中有个内置函数叫round()，用于进行四舍五入的运算，所以可以使用round()这个函数限制运算结果保留位数，去掉不确定尾数。

 >>> round(0.1 + 0.2, 3)
0.3
>>> round(0.1 + 0.2, 3) == 0.3
True

3.复数类型

复数类型表示数学中的复数。复数使用a+bj的形式表示，称为实部和虚部。其中j称为“虚部单位”，它被定义为j=√(-1)。

复数举例：11.3+4j -5.6+7j 1.23e-4+5.67e+89j

在Python中，复数采用(a,b)表示a+bj，a表示实部，b表示虚部，虚部通过后缀“J”或“j”来表示。当b等于1时，1不能省略，采用 1j表示复数，而j则表示Python程序中的一个变量。

复数类型中实部和虚部都是浮点类型，对于复数z，可以用z.real和z.imag分别获取实数部分和虚数部分。

print((1.23e4 + 5.67e4j).real)
print((1.23e4 + 5.67e4j).imag)
print(1.23e4 + 5.67e4j.imag)

output:
12300.0
56700.0
69000.0

二、布尔类型

布尔类型 用来表示真或假

True 表示真
False表示假
布尔值可以转化为整数
- True:1
- False:0

# -*- coding: utf-8 -*-
# @File  : demo.py
# @author: Flyme awei 
# @email : 1071505897@qq.com
# @Time  : 2022/8/3 23:28

f1 = True
f2 = False
print(f1, type(f1))
print(f2, type(f2))

# True <class 'bool'>
# False <class 'bool'>

三、字符串类型

字符串又被称为不可变的字符序列

可以使用单引号:' '双引号:" "三引号:''' ''' 或:""" """来定义，单引号和双引号定义的字符串必须在一行，三引号定义的字符串可以分布在连续的多行

# -*- coding: utf-8 -*-
# @File  : demo.py
# @author: Flyme awei 
# @email : 1071505897@qq.com
# @Time  : 2022/8/3 23:28

print('我用python')
print("我用python")
print('''我用python''')

print(type('我用python'))
print(type("我用python"))
print(type('''我用python'''))

output:
'''
我用python
我用python
我用python
<class 'str'>
<class 'str'>
<class 'str'>
'''

四、数据类型转化

数据类型转换：将不同类型的数据拼接在一起

函数名	作用	注意事项	举例
`str()`	将其它类型转换为字符串	也可用引号转换	`str(123)` ?`'123'`
`int()`	将其它类型转转换为整型	文字类和小数类字符串，无法转换为整数; 浮点数转为整数：抹零取整	`int('123')`
`float()`	将其它类型转换为浮点数	整数转为浮点数，末尾为`.0`	`float(9)`

# -*- coding: utf-8 -*-
# @File  : demo.py
# @author: Flyme awei 
# @email : 1071505897@qq.com
# @Time  : 2022/8/3 23:28

"""
str() 将其它类型转换为字符串类型
"""
print(str(123))
print(type(str(123)))

"""
int() 其它类型转换为整型
    1.文字类 和 小数类字符串 无法转换为整型
    2.浮点数转为整数抹零取整
"""
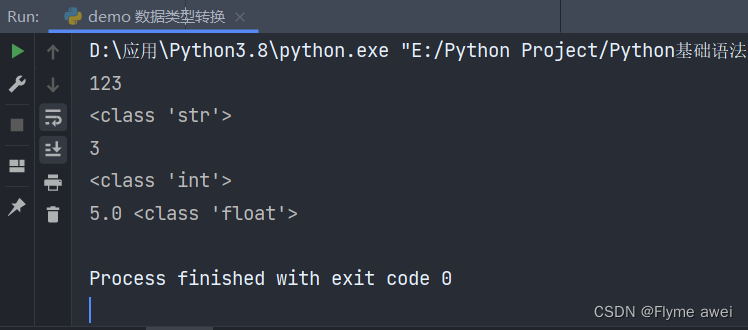
print(int(3.22244))

"""
float() 将其它类型转换为浮点数
    1.文字无法转换
    2.整数转换为浮点数.末尾为 .0  
    """
print(type(5))
print(float(5), type(float(5)))