之前学线性代数的时候碰到过微分的情况,但那个时候还没详细解释微分方程和矩阵之间的关系,这次又碰到了,遗憾的是也没有说,于是查了写资料,特此说明。
主要参考:斐波那契数列通项推导过程中凭什么定理断定它能写成两个等比数列的和? - 知乎
听说线性代数可以在高中降维打击数列、圆锥曲线,具体是怎么应用的? - 知乎

?这部分是显然的。

?
?这里的显然是这样,假设存在第k+1个基本解,那么这些基本解构成的矩阵和向量c1,...ck+1的乘积是零空间。而c1,....c(k+1)不全为0,所以这些解线性相关。

?这里提到了特征多项式,我们复习下:

?有个概念之后还需要仔细理解

?因为特征向量不能为0,所以这个兰大E-A应该是一个奇异矩阵,它的行列式为0.

?这个代换其实不太好理解,首先,把a(n+k-1)看成a1(n), a(n+k-2)看成a2(n)。。。。
重点是a1(n+1) 就是a(n+k),刚好是等式左边。
那么a2(n+1)就是a(n+k-1),刚好是a1(n)
同理推出后面。

?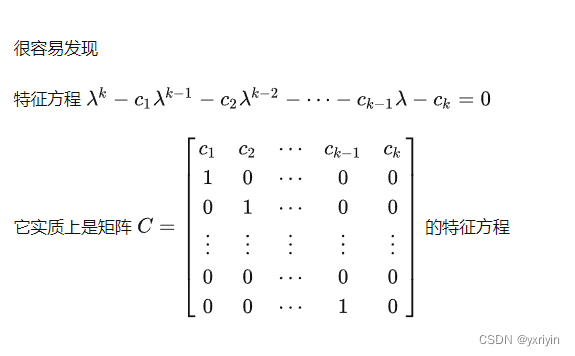
?这个按理应该是求C-浪大I的行列式
[c1-λ, c2, c3.....ck]
[1,? ? ? -λ,? ?0.....? ? ? ? 0]
[0,? ? ? ?1,? -λ.....? ? ? ? 0]
....
[0,0,....? ? ? ? ? ?1,-λ]
然后按照挑选法算行列式的值,
主要是第一行,每个元素单独选过去,易得:
(c1-λ) *?λ^k-1 + c2 *?λ ^ k -2 + c3 *?λ^k-3 + .....ck = 0
其实没那么易得啊。
 ?
?
?
?带入验算,确实如此。特征子空间是一维,说明这个特征值下对应的只有这一个特征向量。

?这个可以用反证法推理是一维的。
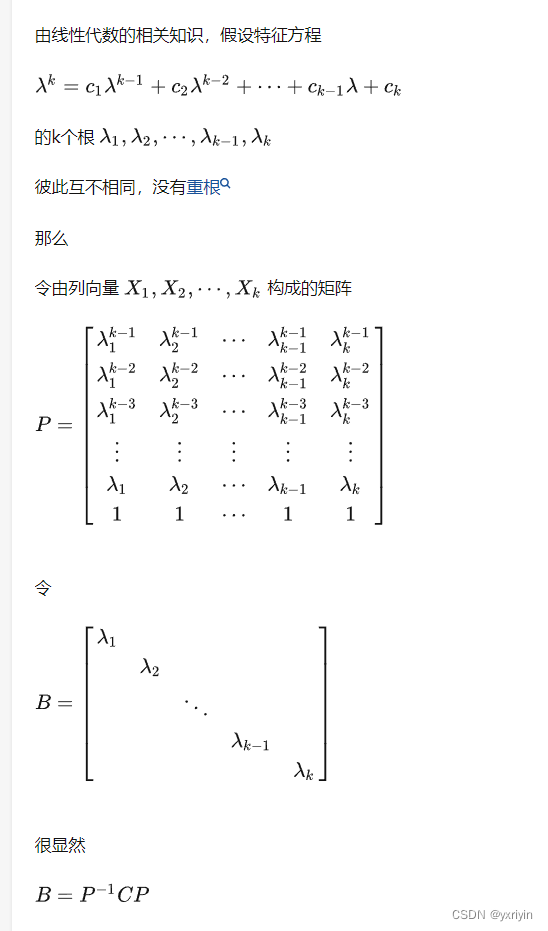
?这是可对角化矩阵的特征向量分解。
我们先用下面这个来理解:

?这里的S就是特征向量构成的矩阵,朗达就是B,P就是S。
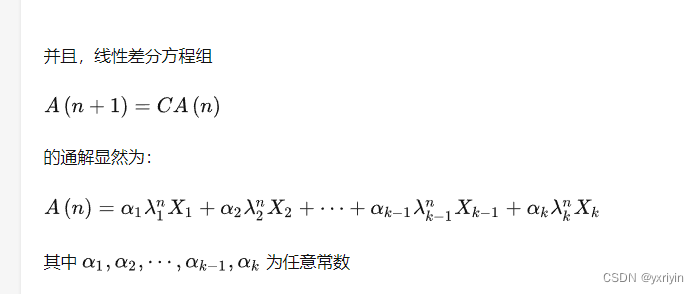
?假定A(n) = 朗达1^nX1
那么CA(n) = 朗达1^n * CX1 = 朗达1^n * 朗达1 X1 = langda1^(n+1) X1? = A(n+1)
带入验算倒是对的。



 ?
?
?仔细理解,我们把原来的差分方程变成了A(n+1) = A(n)这样的形式。

?
?这样,算是接上了。

 ?
?
?
?