开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> Python知识库 -> Python 排序 -> 正文阅读

[Python知识库]Python 排序

Python 排序

Python list 内置 sort() 方法 用来排序，也可以用 python 内置的 全局 sorted() 方法 来对可迭代的序列排序生成新的序列。

List sort() 方法

sort() 函数用于对原列表进行排序（原地排序），如果指定参数，则使用比较函数指定的比较函数。

list.sort( key=None, reverse=False)

key – 主要是用来进行比较的元素，只有一个参数，具体的函数的参数就是取自于可迭代对象中，指定可迭代对象中的一个元素来进行排序。
reverse – 排序规则，reverse = True 降序， reverse = False 升序（默认）。
该方法没有返回值，但是会对列表的对象进行排序。

aList = ['Google', 'Runoob', 'Taobao', 'Facebook']
aList.sort()
print ( "List : ", aList)

以上实例输出结果如下：

List :  ['Facebook', 'Google', 'Runoob', 'Taobao']

以下实例降序输出列表：

vowels = ['e', 'a', 'u', 'o', 'i']
# 降序
vowels.sort(reverse=True)
# 输出结果
print ( '降序输出:', vowels )

以上实例输出结果如下：

降序输出: [‘u’, ‘o’, ‘i’, ‘e’, ‘a’]

以下实例演示了通过指定列表中的元素排序来输出列表：

# 获取列表的第二个元素
def takeSecond(elem):
    return elem[1]
# 列表
random = [(2, 2), (3, 4), (4, 1), (1, 3)]
# 指定第二个元素排序
random.sort(key=takeSecond)
# 输出类别
print ('排序列表：', random)

以上实例输出结果如下：

排序列表：[(4, 1), (2, 2), (1, 3), (3, 4)]?

Python sorted() 内置函数

sorted() 函数对所有可迭代的对象进行排序操作。

sort 与 sorted 区别：

sort 是应用在 list 上的方法，sorted 可以对所有可迭代的对象进行排序操作。
list 的 sort 方法返回的是对已经存在的列表进行操作，而内建函数 sorted 方法返回的是一个新的
list，而不是在原来的基础上进行的操作。

sorted(iterable, key=None, reverse=False)

iterable – 可迭代对象。
key – 主要是用来进行比较的元素，只有一个参数，具体的函数的参数就是取自于可迭代对象中，指定可迭代对象中的一个元素来进行排序。
reverse – 排序规则，reverse = True 降序， reverse = False 升序（默认）。
返回重新排序的列表。

以下实例展示了 sorted 的最简单的使用方法：

>>>sorted([5, 2, 3, 1, 4])
[1, 2, 3, 4, 5] # 默认为升序

你也可以使用 list 的 list.sort() 方法。这个方法会修改原始的 list（返回值为None）。通常这个方法不如 sorted() 方便-如果你不需要原始的 list，list.sort() 方法效率会稍微高一些。

>>> a=[5,2,3,1,4]
>>> a.sort()
>>> a
[1,2,3,4,5]

另一个区别在于list.sort() 方法只为 list 定义。而 sorted() 函数可以接收任何的 iterable。

>>> sorted({1: 'D', 2: 'B', 3: 'B', 4: 'E', 5: 'A'})
[1, 2, 3, 4, 5]

利用 key 进行倒序排序

>>> example_list = [5, 0, 6, 1, 2, 7, 3, 4]
>>> result_list = sorted(example_list, key=lambda x: x*-1)
>>> print(result_list) [7, 6, 5, 4, 3, 2, 1, 0]

要进行反向排序，也通过传入第三个参数 reverse=True：

>>>example_list = [5, 0, 6, 1, 2, 7, 3, 4] 
>>> sorted(example_list, reverse=True) 
[7, 6, 5, 4, 3, 2, 1, 0]

sorted 的应用，也可以通过 key 的值来进行数组/字典的排序，比如：

array = [{"age":20,"name":"a"},{"age":25,"name":"b"},{"age":10,"name":"c"}]
array = sorted(array,key=lambda x:x["age"])
print(array)

输出结果：

[{'age': 10, 'name': 'c'}, {'age': 20, 'name': 'a'}, {'age': 25, 'name': 'b'}]

多列排序

先按照成绩降序排序，相同成绩的按照名字升序排序：

d1 = [{'name':'alice', 'score':38}, {'name':'bob', 'score':18}, {'name':'darl', 'score':28}, {'name':'christ', 'score':28}]
l = sorted(d1, key=lambda x:(-x['score'], x['name']))
print(l)

输出结果：

[{'name': 'alice', 'score': 38}, {'name': 'christ', 'score': 28}, {'name': 'darl', 'score': 28}, {'name': 'bob', 'score': 18}]

★164. 最大间距

Leetcode
基于比较的排序算法（快速排序、归并排序等）均需要 $O(N\log N)$ 的时间复杂度。
桶排序、计数排序、基数排序这三个算法是不基于比较的排序算法，都不涉及元素之间的比较操作。

方法一：基数排序

class Solution:
    def maximumGap(self, nums: List[int]) -> int:

        n = len(nums)
        if n < 2:  return 0
        digit = len(str(max(nums)))
        w = 1 # 用于取各位数字
        d = defaultdict(list)
       
        for k in range(digit):            
            for num in nums:
                d[num // w % 10].append(num) ## w 用 10 ** k 时间翻倍
                
            nums[:] = [num for g in range(10) for num in d[g]]

            w *= 10
            d.clear()

        return max(nums[i] - nums[i-1] for i in range(1, n))

class Solution:
    # 基数排序
    def radixSort(self, nums):
        digit = len(str(max(nums)))
      
        buckets = defaultdict(list)
        w = 1
        for k in range(digit):            
            for num in nums:
                buckets[num // w % 10].append(num)
                
            nums[:] = [num for g in range(10) for num in buckets[g]]
            w *= 10
            buckets.clear()

    def maximumGap(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2: return 0
        self.radixSort(nums)
        return max(nums[i] - nums[i-1] for i in range(1, n))

方法二：桶排序

nums 长度为 n, 最大值和最小值为 max_、min_。
相邻数字的最大间距不会小于 $?(ma x ? min) / (n ? 1)?$ 。也就是不会落在同一个桶中，只可能在不同的桶产生。
桶的大小：bucketSize = max(1, (max_ - min_) // (n - 1))
数量：bucketsLen = (max_ - min_) // bucket_size + 1

桶排序，只用考虑桶间的排序，不用考虑桶内的排序，用后一个桶的最小值减前一个桶的最大值，可以得到最大间距。

class Solution:
    # 桶排序的思想
    def bucketSort(self, nums): 
        n = len(nums)       
        max_ = max(nums)
        min_ = min(nums)
        max_gap = 0        
        bucket_size = max(1, (max_ - min_) // (n - 1))
        # if max_ == min_: return 0 # [1,1,1,1]
        # bucket_size = ceil((max_ - min_) / (n - 1))
        buckets_len = (max_ - min_) // bucket_size + 1
        buckets =[[] for _ in range(buckets_len)]
        
        # 把数字放入桶中
        for num in nums:
            loc = (num - min_) // bucket_size
            buckets[loc].append(num)
        
        # 遍历桶更新答案
        buckets = [b for b in buckets if b] # 移除空桶
        prev_max = max(buckets[0])
        for b in buckets[1:]:
            max_gap = max(max_gap, min(b) - prev_max)
            prev_max = max(b)
                
        return max_gap

    def maximumGap(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2: return 0       
        return self.bucketSort(nums)

https://zhuanlan.zhihu.com/p/357603773

179. 最大数

Leetcode

方法一：排序

两个数字对应的字符串 a 和 b，如果字典序 a + b > b + a，此时 a 排在 b 的前面即可获得更大值
示例：a = 3, b = 32,两者拼接的值：332 > 323，所以 3 应排在 3 2前面

class Solution:
    def largestNumber(self, nums: List[int]) -> str:
        n=len(nums)
        nums=list(map(str,nums))
        for i in range(n):
            for j in range(i+1,n):
                if nums[i]+nums[j] < nums[j]+nums[i]:
                    nums[i],nums[j] = nums[j],nums[i]
        
        return str(int("".join(nums)))

方法二：cmp_to_key

利用 cmp_to_key 函数，传入两个参数(x, y)对应于(self, other),这里的 self 表示当前的数，而 other 是前面已经出现比较过的对象。比如 arr = [3, 32]，此时 self 为 32，other 为 3，即 x = 32, y = 3,这里与惯性思维是相反的.
示例：x = 32, y = 3,或者说 y 为数组前面的数，x 为数组后面的数。要使得构造的数更大，需要满足条件：前面的数 + 后面的数 > 后面的数 + 前面的数，即 y + x > x + y 返回 1 成立，即 332 > 323 成立，此时 3 出现在 32 前面

class Solution:
    def largestNumber(self, nums: List[int]) -> str:
        def cmp(x,y): return 1 if x+y<y+x else -1
        nums=list(map(str,nums))
        nums.sort(key=cmp_to_key(cmp))
        res= str(int("".join(nums)))
        return res

class Solution:
    def largestNumber(self, nums: List[int]) -> str:
        '''
        nums = map(str, nums)
        # x = sorted(nums, key=cmp_to_key(lambda x, y:1 if x+y >= y+x else -1), reverse=True)
        x = sorted(nums, key=cmp_to_key(lambda x, y:int(x+y)-int(y+x)), reverse=True)
        return ''.join(x) if x[0] != '0' else '0'

        '''
        ret = ''
        n = len(nums)
        s = map(str, nums)
        s = sorted(s, reverse=True)
        for i in range(n-1):
            for j in range(i+1, n):
                if int(s[i] + s[j]) < int(s[j] + s[i]):
                    s[i], s[j] = s[j], s[i]
            ret += s[i]
        ret += s[-1]
        return ret[0] if int(ret) == 0 else ret
        '''    
               
        #from functools import cmp_to_key

        ret = map(str, nums)

        def cmp(a, b):
            if a + b >= b + a:
                return 1
            else:
                return -1
                
        ret = sorted(ret, key=cmp_to_key(cmp), reverse=True)
        return ''.join(ret) if ret[0] != '0' else '0'
        '''

506. 相对名次

Leetcode

class Solution:
    def findRelativeRanks(self, score: List[int]) -> List[str]:
        x = sorted(score, reverse=True)
        
        n = len(score)
        d = {x[i]:str(i + 1) for i in range(n)}
        
        d[x[0]] = "Gold Medal"
        if n > 1: d[x[1]] = "Silver Medal"
        if n > 2: d[x[2]] = "Bronze Medal"
        
        return [d[i] for i in score]

786. 第 K 个最小的素数分数

Leetcode

方法一：自定义排序

直接对它们的值进行比较，但这会产生浮点数的计算，降低程序的效率，并且可能会引入浮点数误差。一种可行的替代方法是用： $\times d < b \times c$ 来替代 $\dfrac{a}{b} < \dfrac{c}{d}$ 的判断，二者是等价的。(事实上变的更慢)

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        # 自定义排序
        def cmp(x, y):
            return -1 if x[0] * y[1] < x[1] * y[0] else 1

        res, n = [], len(arr)

        for i in range(n):
            for j in range(i + 1, n):
                res.append([arr[i], arr[j]])

        # res.sort(key=lambda x:x[0]/x[1]) ## 直接比较分数值  
        res.sort(key=cmp_to_key(cmp)) # 变的更慢

        return res[k - 1]

方法二：优先队列（堆）

## 自定义比较方法
class Frac:
    def __init__(self, idx: int, idy: int, x: int, y: int) -> None:
        self.idx = idx
        self.idy = idy
        self.x = x # arr[idx]
        self.y = y

    def __lt__(self, other: "Frac") -> bool:
        return self.x * other.y < self.y * other.x

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        n = len(arr)
        q = [Frac(0, i, arr[0], arr[i]) for i in range(1, n)]
        heapq.heapify(q)

        for _ in range(k - 1):
            frac = heapq.heappop(q)
            i, j = frac.idx, frac.idy
            if i + 1 < j:
                heapq.heappush(q, Frac(i + 1, j, arr[i + 1], arr[j]))
        
        return [q[0].x, q[0].y]
        
## 直接比较分数值        
class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        pq = []
        for i in range(1, len(arr)):
            # 分数、分子、分母坐标 先把首元素构成的分数推入顶
            heapq.heappush(pq, (arr[0]/arr[i], 0, i))

        for _ in range(k):
            _, i, j = heapq.heappop(pq)
            if i < j - 1:
                heapq.heappush(pq, (arr[i + 1]/arr[j], i + 1, j))
                
        return [arr[i], arr[j]]

## heapq.nsmallest
class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        n = len(arr)
        res = [(i, j) for i in range(n) for j in range(i + 1, n)]        
        ans = heapq.nsmallest(k, res, key=lambda x:arr[x[0]]/arr[x[1]])
        return [arr[ans[-1][0]], arr[ans[-1][1]]]

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        n = len(arr)
        res = [(arr[i], arr[j]) for i in range(n) for j in range(i + 1, n)]        
        ans = heapq.nsmallest(k, res, key=lambda x:x[0]/x[1])
        return [ans[-1][0], ans[-1][1]]

方法三：(浮点数的)二分查找 + 双指针

二分搜索范围 (0, 1)，假设取一个数 mid，小于 mid 的分数个数为 count：

若 count < k：需要增大 mid
若 count > k：需要减小 mid
若 count = k：返回最大的分数

定义双指针，i 指向分子，j 指向分母，因为列表递增排列，遍历 j，只需找到第一个不满足 arr[i] / arr[j] < mid 的 i，累加到 count 中。

注意，寻找i的过程中，记录最大的分数。

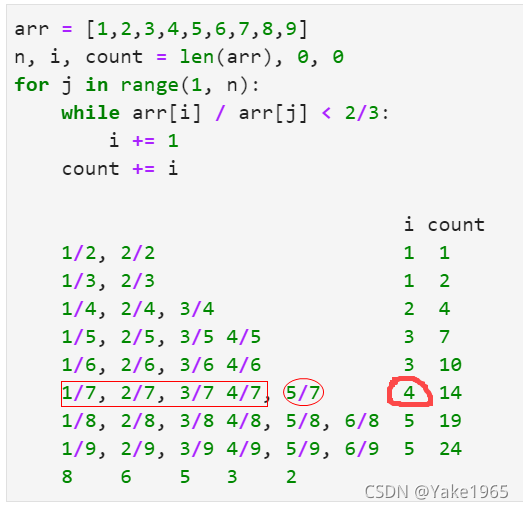
n, i, count = len(arr), 0, 0
for j in range(1, n):    
    while arr[i] / arr[j] < 2/3:        
        i += 1    
    count += i ## i 用的很妙

在这里插入图片描述

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        n = len(arr)
        left, right = 0, 1

        while True:
            mid = (left + right) / 2
            i = count = 0 # count 小于 mid 的分数的个数
            x, y = 0, 1 # 记录最大的分数的分子分母
            
            for j in range(1, n):
                while arr[i] / arr[j] < mid:
                    if arr[i] * y > arr[j] * x:
                        x, y = arr[i], arr[j]
                    i += 1
                    
                count += i

            if count == k:  return [x, y]            
            if count < k: left = mid
            else: right = mid

方法四：组合

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        return sorted(combinations(arr,2),key=lambda x:x[0]/x[1])[k-1]