PyTorch基础知识

张量及其运算
自动求导简介

张量及其运算

Scalar： 3 Vector: $\begin{bmatrix}1\\2 \end{bmatrix}$

Matrix: $\begin{bmatrix} 1&2 \\ 3&4 \end{bmatrix}$ Tensor: $\begin{bmatrix}\begin{bmatrix}1&2 \end{bmatrix} \begin{bmatrix}3&2 \end{bmatrix} \\ \begin{bmatrix}5&4\end{bmatrix}\begin{bmatrix}1&7 \end{bmatrix}\end{bmatrix}$

以上分别是：标量，向量，矩阵以及张量。

也可以说向量是一维张量，矩阵是二维张量，还可以有四维，五维张量甚至n维张量，张量不受到维度的限制。用于“记录”不同维度数据。

在图像的运算中经常涉及到高维数据的运算，因此使用张量来进行计算。与数学中的张量有区别，是pytorch中运算的基础单元。

基本计算

tensor创建

使用torch.tensor()创建张量。

#创建tensor,dtype指定数据类型，类型需要匹配
a=torch.tensor(1.0,dtype=torch.float)
b=torch.tensor(1,dtype=torch.long)
print(a,b)

#使用指定类型随机初始化指定大小的tensor
c=torch.FloatTensor(2,3)
print(c)

#将array转为tensor
d=np.array([[1,2,3],[4,5,6]])
print(d)
e=torch.tensor(d)
print(e)
f=torch.from_numpy(d)
print(f)
#将tensor转回array
g=e.numpy()
print(g)

#常见的构造函数
h=torch.rand(2,3)#2*3大小的随机矩阵
print(h)
i=torch.ones(2,3)#2*3大小的1矩阵
print(i)
j=torch.zeros(2,3)#0矩阵
print(j)
k=torch.arange(0,10,2)#一维0-10，间隔为2
print(k)

请添加图片描述

维度信息查看

#查询维度信息shape,size()
print(k.shape)
print(k.size())

在这里插入图片描述

基本运算

#基本运算
l = torch.add(h,i)
print(l)

请添加图片描述

改变形状

#改变形状view,-1维度会自动计算
print(l.view(3,2))
print(l.view(-1,2))

在这里插入图片描述

广播机制

#tensor的广播机制
#对于不同维度的运算，自动转为可计算张量
p=torch.arange(1, 3).view(1, 2)
print(p)
q=torch.arange(1, 4).view(3, 1)
print(q)
print(p + q)#[[1,2][1,2][1,2]]+[[1,1][2,2][3,3]]

在这里插入图片描述

自动求导

机器学习的主要目的，求解损失函数平面最小值。通过不断的求导数更替寻找最优解。

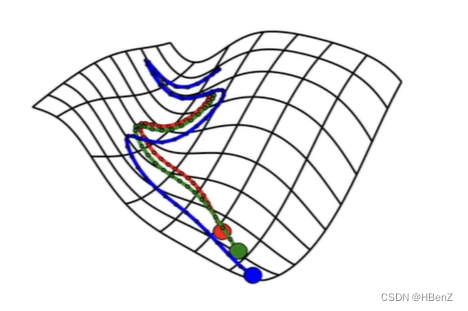
在这里插入图片描述

模型训练过程回顾

数据输入，正向传播：正向计算结果值
计算损失函数：根据定义的损失函数公式计算损失
损失函数的反向传播：对损失函数模型求导，以找到最小损失
模型参数更新：根据反向传播数据修正模型中的参数

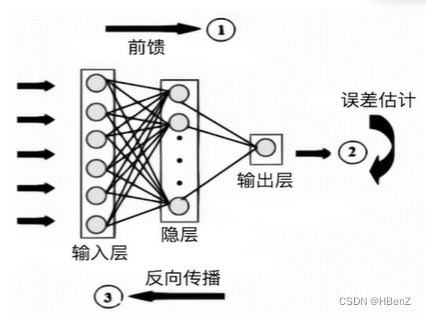
在这里插入图片描述

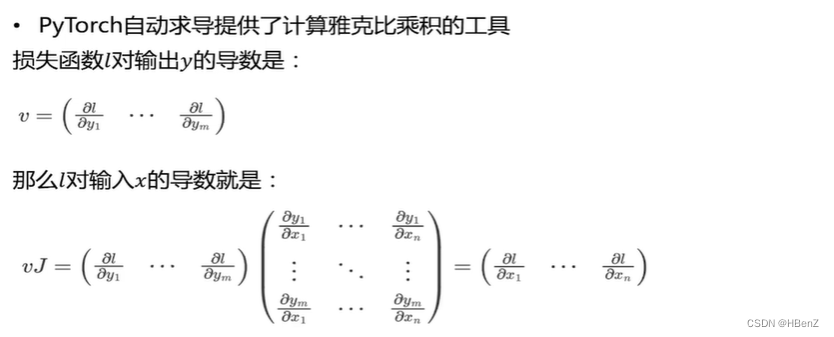
反向传播—数学基础

多元函数求导——雅可比矩阵：

$\begin{Bmatrix} \frac{\partial y_1}{\partial x_1}&{\cdots}&\frac{\partial y_1}{\partial x_1}\\ {\vdots}&{\ddots}&{\vdots} \\ \frac{\partial y_1}{\partial x_1}&{\cdots}&\frac{\partial y_1}{\partial x_1} \end{Bmatrix}$

复合函数求导链式法则：高数中的

若 $h (x) = f (g (x)) 则 h^{'} (x) = f^{'} (g (x)) ? g^{'} (x)$

动态计算图(DCG)

由节点和边构成，节点是张量或者function，边表示节点之间的关系。

举个栗子：z=x*y

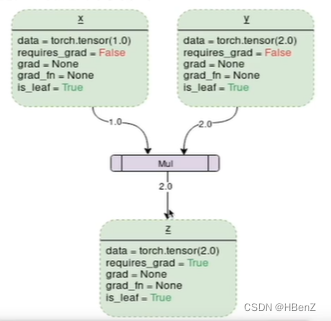
在这里插入图片描述

每一个绿块都表示一个node，中间是function。可以看到在每个node都有相关信息data：表示数据，requires_grad=False：表示不可求导,grad=求导值，grad_fn=求导方法，is_leaf=True:求导终点(is_leaf=True,requires_grad=False)

动态：

第一层含义是：计算图的正向传播是立即执行的。无需等待完整的计算图创建完毕，每条语句都会在计算图中动态添加节点和边，并立即执行正向传播得到计算结果。

第二层含义是：计算图在反向传播后立即销毁。下次调用需要重新构建计算图。如果在程序中使用了backward方法执行了反向传播，或者利用torch.autograd.grad方法计算了梯度，那么创建的计算图会被立即销毁，释放存储空间，下次调用需要重新创建。

代码演示

#前向传播,定义两个张量，设置为可求导
x1=torch.tensor(1.0,requires_grad=True)
x2=torch.tensor(2.0,requires_grad=True)
y=x1+2*x2
print(y)
#y的描述中grad_fn=ADDBackward0

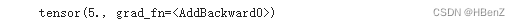
#前项传播
y=x1+2*x2
#反向传播
y.backward()
#反向传播之后，会进行梯度更新
print(x1.grad.data)
print(x2.grad.data)
#导数的累计，重复上面操作，grad增加
y=x1+2*x2
y.backward()
print(x1.grad.data)
print(x2.grad.data)
#因此计算时需要清空grad避免累计，可通过optimizer实现