由Black-Scholes在1973年提出的期权定价模型,可以说是现代财务的起始点。我们首先以一个简单的欧式(Vanilla)期权为例,说明如何使用QuantLib套件,简单的完成价格与Greeks的计算。并且呼叫隐含波动性的计算函数,轻易的算出这个交易时重要的参数。下表List 1_1便是整个程序的列表。
程序分为7个段落,第一段为定价环境参数设定,第二段为市场参数设定,第三段金融工具参数设定,第四段为定价引擎的设定,第五段为定价结果产出,第六段为敏感性结果产出,第七段为隐含波动性的计算产出。
#001 import QuantLib as ql
# 1.Enviroment
#003 settings = ql.Settings.instance()
#004 evDate = ql.Date(8, 6, 2021)
#005 settings.setEvaluationDate(evDate)
#006 Cal = ql.NullCalendar()
#007 DC365 = ql.Actual365Fixed()
#008 settlementDays = 0
#009 refDate = Cal.advance(evDate, settlementDays, ql.Days, ql.Following, False)
#010 maturity = Cal.advance(refDate, 1, ql.Years, ql.Following, False)
#011
# 2.Market Data
#013 S0 = 100
#014 QS = ql.SimpleQuote(S0)
#015 h_QS = ql.QuoteHandle(QS)
#016 r = 0.06
#017 rTS = ql.FlatForward(settlementDays, Cal, r, DC365, ql.Compounded, ql.Annual)
#018 h_rTS = ql.YieldTermStructureHandle(rTS)
#019 q = 0.03
#020 qTS = ql.FlatForward(settlementDays, Cal, q, DC365, ql.Compounded, ql.Annual)
#021 h_qTS = ql.YieldTermStructureHandle(qTS)
#022 vol = 0.3
#023 volTS = ql.BlackConstantVol(evDate, Cal, vol, DC365)
#024 h_volTS = ql.BlackVolTermStructureHandle(volTS)
#025 GBSProcess = ql.GeneralizedBlackScholesProcess(h_QS, h_qTS, h_rTS, h_volTS)
#026
# 3.Instrument
#028 europeanExer = ql.EuropeanExercise(maturity)
#029 strike = 100.0
#030 optType = ql.Option.Call
#031 vanillaPayoff = ql.PlainVanillaPayoff(optType, strike)
#032 anEuroOption = ql.EuropeanOption(vanillaPayoff, europeanExer)
#033
# 4.Engine
#035 AEE = ql.AnalyticEuropeanEngine(GBSProcess)
#036 anEuroOption.setPricingEngine(AEE)
#037
# 5.MTM
#039 Value = anEuroOption.NPV()
#040 print("MTM: ", Value)
#041
# 6.Greeks
#043 Delta = anEuroOption.delta()
#044 print("Delta: ", Delta)
#045 Gamma = anEuroOption.gamma()
#046 print("Gamma: ", Gamma)
#047 Vega = anEuroOption.vega()
#048 print("Vega: ", Vega)
#049
#050 Theta = anEuroOption.theta()
#051 print("Theta: ", Theta)
#052 Rho = anEuroOption.rho()
#053 print("Rho: ", Rho)
#054 DividendRho = anEuroOption.dividendRho()
#055 print("Dividend Rho: ", DividendRho)
#056
# 7.Implied Volatility
#058 Price1 = 15.0
#059 vol1 = anEuroOption.impliedVolatility(Price1, GBSProcess)
#060 print("Implied Vol at Price ", Price1,": ", vol1)
#061 Price2 = 10.0
#062 vol2 = anEuroOption.impliedVolatility(Price2, GBSProcess)
#063 print("Implied Vol at Price ", Price2,": ", vol2)
List 1-1
#001首先载入QuantLib套件,并简称为ql。#003产生环境设定对象settings,#004产生定价基准日evDate为2021/6/8,#005将定价基准日evDate设定到settings中。#006产生一个没有假日的日历Cal。#007建立一个Actual365的计息方式对象。#008令T+0的交割方式。#009使用Cal推算真正的交割日期refDate。#010推算一年后到期的日期maturity。
#013设定标的资产价格S0为100.0。#014产生标的资产的报价对象Q_S。#015产生标的资产报价对象的握柄(Handle)hQ_S。#016令资金成本r为6%。#017以r产生一条水平的利率期限结构对象rTS。#018以rTS产生水平的利率期限结构对象的握柄h_rTS。#019令资产收益q为3%。#020以q产生一条水平的收益期限结构对象qTS。#021以qTS产生水平的收益期限结构对象的握柄h_qTS。#022令资产波动性vol为30%。#023以vol产生一条水平的波动性期限结构对象volTS。#024以volTS产生水平的波动性期限结构对象的握柄h_volTS。#025用h_QS、h_rTS、h_qTS、h_volTS四个握柄,产生一般化的Black-Scholes过程对象GBSProcess。
#028以maturity产生一个欧式到期对象。#029设定执行价格strike为100.0。#030设定期权为Call类别optType。#031产生一个欧式期权的偿付对象vanillaPayoff。#032以optType与vanillaPayoff产生一个欧式期权anEuroOption。
#035产生一个解析解的计算引擎AEE。#036将计算引擎AEE设定给期权anEuroOption。
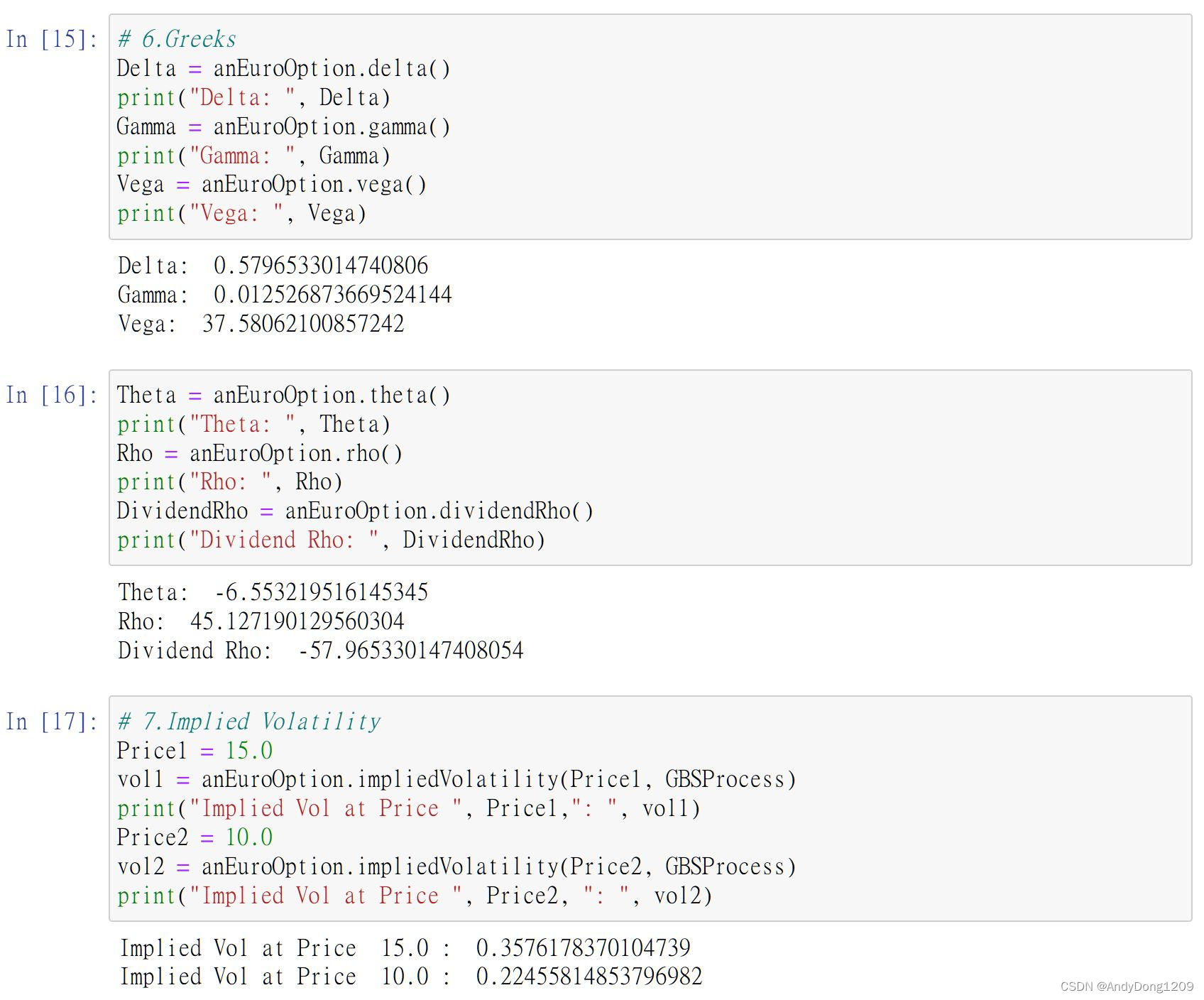
#039呼叫期权的NPV()方法计算价值,并将其印出。#043~#055分别叫用各个Greeks的方法,并印出结果。
#058设定价格Price1=15.0,#059并以此计算对应之隐含波动性vol1。#061设定价格Price2=10.0,#062并以此计算对应之隐含波动性vol2。
虽然程序有些长,但每一行的程序对应着实际金融计算的相关逻辑,这使得QuantLib的程序代码,可以非常正确的计算出真实世界的金融资产价格。尤其像是日历的假日推算、计息折现方式、与期限结构的设定,都与真实的金融计算一致。事实上QuantLib是一个以银行交易室实务使用为目标,开发出来的链接库。
QuantLib是一个面向对象的链接库,本书的前半部分将仔细说明这些金融市场的对象,让读者了解上述程序运作的原则,并自行加以调整变化。然后再进一步介绍其他各类的新奇(Exotic)期权,如二元期权、亚洲式期权、阻隔期权。以及各类的定价模型,如树状模型、有限差分法、蒙地卡罗模拟法。
事实上,QuantLib里面还有进阶的随机波动性模型,如Heston、SABR等模型。甚至包含更复杂的具有跳动的随机波动性模型(Stochastic Volatility Model with Jumps),如Bates模型,或是随机的局部波动性模型(Stochastic Local Volatility Model)。可以说实务上会使用的模型,它大概都有开发。如果能充分使用QuantLib,必能扩大我们金融计算的能力,当然它是免费的开源工具。
下图为在Jupyter Notebook中执行产出的画面。程序可在Github下载, GitHub - andydong1209/QuantLib_Python。

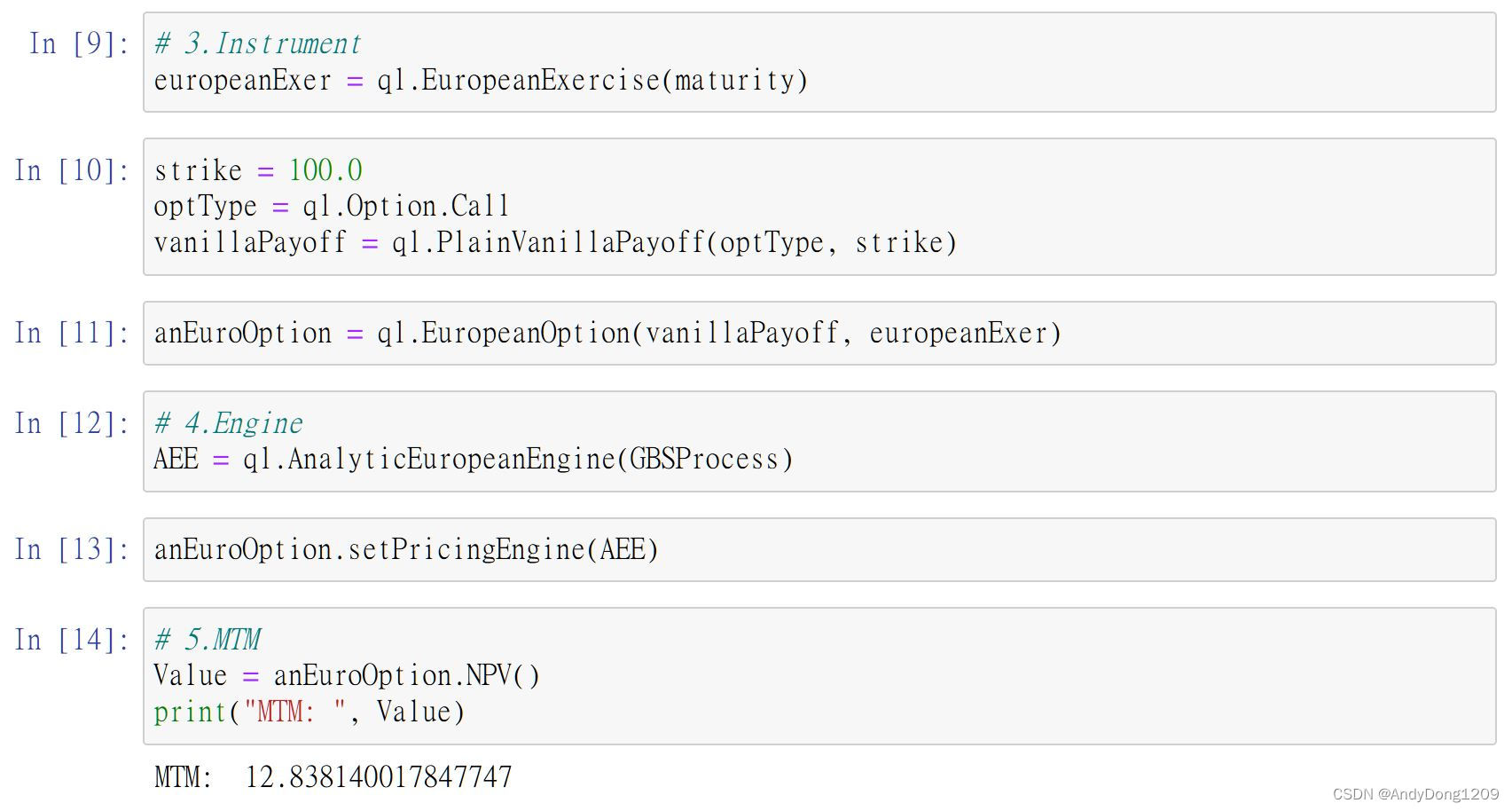 ?
?
?