∣ ? 斜面交点处问题 ? ? Nightguard ? Series. ? ∣ \begin{vmatrix}\Huge{\textsf{ 斜面交点处问题 }}\\\texttt{ Nightguard Series. }\end{vmatrix} ∣ ∣??斜面交点处问题??Nightguard?Series.??∣ ∣?
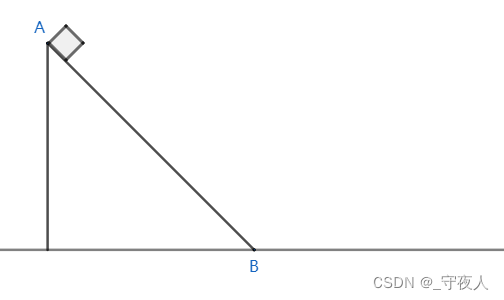
如图,光滑平面上固定了一个高为 H H H 的光滑斜面,斜面倾角为 θ \theta θ,末端与平面交点为 B B B。斜面最高点 A A A 处有一质量为 m m m 的小物块,物块由静止状态开始从 A A A 沿斜面滑下,经过 B B B 点后 立刻贴紧平面继续运动 ,小物块可视为质点,试分析小物块的运动过程。
可是,这不就是机械能守恒吗?
请注意:斜面与平面交界处无光滑曲面连接,且发生非弹性碰撞,这意味着需要考虑小物块的机械能、动量损失。
那要如何操作呢?
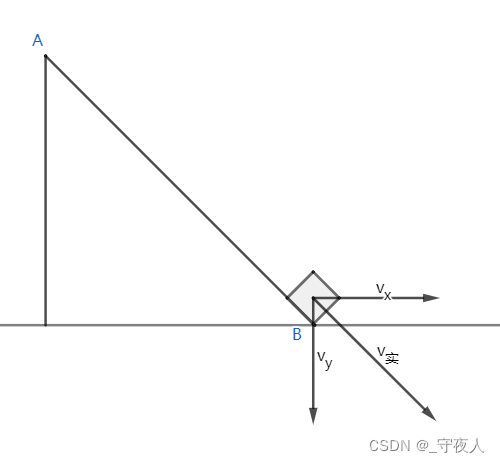
注意小物块与斜面碰撞的瞬间之前,小物块速度方向沿斜面向下,碰撞瞬间小物块速度方向变为水平向右,因为小物块不可能运动到平面之下(废话),所以可以发现小物块在碰撞瞬间损失了竖直向下的动量。
法1: 由 A A A 到 B B B 过程中机械能守恒, m g H = 1 2 m v B 2 mgH=\frac{1}{2}mv_B^2 mgH=21?mvB2?;碰后速度 v ′ = v B cos ? θ v'=v_B \cos \theta v′=vB?cosθ,因此
E 损 = 1 2 m v B 2 ? 1 2 m v ′ 2 = 1 2 m v B 2 sin ? 2 θ = sin ? 2 θ m g H . E_{\text{损}}=\frac{1}{2}mv_B^2-\frac{1}{2}mv'^2=\frac{1}{2}m v_B^2\sin^2\theta=\sin^2\theta mgH. E损?=21?mvB2??21?mv′2=21?mvB2?sin2θ=sin2θmgH.
法2:小物块损失竖直向下的速度,竖直向下速度 v = v B sin ? θ v=v_B\sin \theta v=vB?sinθ,因此
E 损 = 1 2 m v B 2 sin ? 2 θ = sin ? 2 θ m g H . E_{\text{损}}=\frac{1}{2}m v_B^2\sin^2\theta=\sin^2\theta mgH. E损?=21?mvB2?sin2θ=sin2θmgH.
然后小物块以 v ′ = c o s θ v B v'=cos\theta v_B v′=cosθvB? 的速度在光滑平面上做匀速直线运动。
现在我们稍微加一点难度,如果斜面粗糙该怎么办呢?
是不是只有碰撞以后在平面上的运动过程改变了呢?
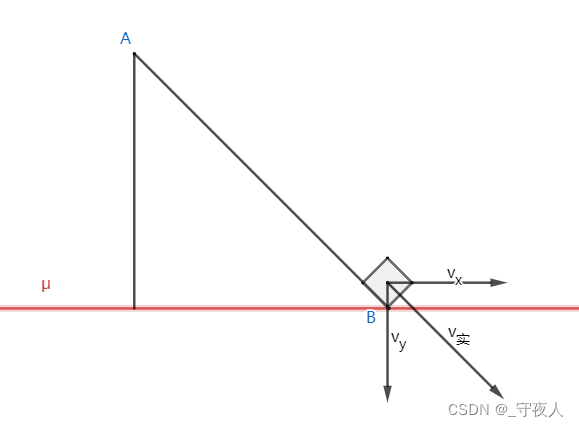
实验结果表明,小物块也有可能停留在斜面的底端。

严谨的实验(大嘘
我们需要更进一步考虑小物块损失机械能的这个过程。
在碰撞的一瞬间,速度并不是瞬间损失的,而是需要弹力 F N F_N FN? 作用一段时间。(这也是动量相关题目常见的考法,通常求一求平均力什么的)在这段时间里,由于平面粗糙,摩擦力会阻碍小物块向右运动,小物块向右的动量损失。 如果在这段时间里,小物块向右的动量比向下的动量先减小到0,则小物块会停止在斜面底端。
首先判断小物块是否会停止在斜面底端:
设小物块向下的动量减小到0所需时间为 t y t_y ty?,向右的动量减小到0所需时间为 t x t_x tx?。
竖直方向上运用动量定理得
( F N ? m g ) t x = m v B sin ? θ (F_N-mg)t_x=mv_B\sin\theta (FN??mg)tx?=mvB?sinθ
水平方向上运用动量定理得
μ ( F N ? m g ) t y = m v B cos ? θ ? m v ′ \mu(F_N-mg)t_y=mv_B\cos\theta-mv' μ(FN??mg)ty?=mvB?cosθ?mv′
如果题目给了 F N F_N FN? 或者任何一个 t t t 事情就好办了QAQ
如果没有,由于碰撞时间很短, F N F_N FN? 很大,所以我们进行一个重力的忽略,令 m g = 0 mg=0 mg=0,两式相除得
t x t y = μ v B sin ? θ v B cos ? θ ? v ′ \frac{t_x}{t_y}=\frac{\mu v_B\sin \theta}{v_B\cos \theta-v'} ty?tx??=vB?cosθ?v′μvB?sinθ?
由于 μ , v B , θ \mu,v_B,\theta μ,vB?,θ 都是定值,因此 t x t y \frac{t_x}{t_y} ty?tx?? 随着 v ′ v' v′ 的减小而减小。当 v ′ = 0 v'=0 v′=0 时,代表小物块会停止在斜面底端,由于我们需要判断小物块是否会停止在斜面底端,因此带入 v ′ = 0 v'=0 v′=0 计算得
t x t y = μ tan ? θ \frac{t_x}{t_y}=\mu \tan \theta ty?tx??=μtanθ
如果 μ tan ? θ ≥ 1 \mu \tan \theta\geq1 μtanθ≥1,则 t x ≥ t y t_x\geq t_y tx?≥ty?,意味着小物块小物块会停止在斜面底端, E 损 = m g H E_{损}=mgH E损?=mgH(全给你损完了是吧)
否则,若代入 v ′ = 0 v'=0 v′=0 计算得 μ tan ? θ < 1 \mu \tan \theta<1 μtanθ<1,则 t x < t y t_x< t_y tx?<ty?,意味着小物块不会停止在斜面底端,这与 v ′ = 0 v'=0 v′=0 矛盾,因此 v ′ ≠ 0 v'\neq0 v′=0,继续计算在平面上继续运动的情况:
易得 t x = t y t_x=t_y tx?=ty?,代入原式化简得
v ′ = v B cos ? θ ? μ v B sin ? θ v'=v_B\cos \theta-\mu v_B\sin \theta v′=vB?cosθ?μvB?sinθ
E 损 = 1 2 m v B 2 ? 1 2 m v ′ 2 E_{\text{损}}=\frac{1}{2}mv_B^2-\frac{1}{2}mv'^2 E损?=21?mvB2??21?mv′2
可以推出 E 损 E_{损} E损? 与 E 总 E_{总} E总? 的关系:
E 损 E 总 = 1 2 m v B 2 ? 1 2 m v ′ 2 1 2 m v B 2 = v B 2 ? ( cos ? θ ? μ sin ? θ ) 2 v B 2 v B 2 = 1 ? ( cos ? θ ? μ sin ? θ ) 2 . \frac{E_{损}}{E_{总}}=\frac{\frac{1}{2}mv_B^2-\frac{1}{2}mv'^2}{\frac{1}{2}mv_B^2}=\frac{v_B^2-(\cos \theta-\mu \sin \theta)^2v_B^2}{v_B^2}=1-(\cos \theta-\mu \sin \theta)^2. E总?E损??=21?mvB2?21?mvB2??21?mv′2?=vB2?vB2??(cosθ?μsinθ)2vB2??=1?(cosθ?μsinθ)2.
代入数值计算即可。
同时, μ tan ? θ ≥ 1 \mu \tan \theta\geq1 μtanθ≥1 可以转化为 θ ≥ arctan ? 1 μ \theta \geq \arctan\frac{1}{\mu} θ≥arctanμ1? , θ \theta θ 高于临界值则必然静止在斜面底端,低于临界值则在平面上继续运动。
这么复杂,以后做这种题不都得PTSD?
笔者从来没在考卷里见过这种题,请大家不用太担心,但还是留个心眼:注意题目所给条件。若未出现以下条件:
-
斜面与平面之间由光滑的圆弧连接
-
经过 B B B 点时速度大小不改变
-
经过 B B B 点时无动能损失
等类似字眼,就稍微注意一下
推测:把看似第一问难度的东西放在最后一问时考虑这些东西。
参考资料 https://www.fx361.com/page/2020/0719/8589242.shtml
练习
1.小物块从平面滑上斜面(同理)
2.https://www.bilibili.com/video/BV1iK4y1Q7mc?p=9(黄夫人)