1 误差反向传播法
能够高效计算权重参数的梯度的方法。
1.1 乘法层的实现 MulLayer , 并且实现例子
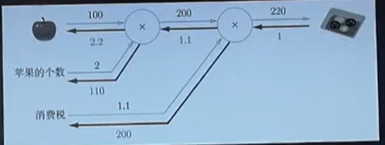
import numpy as np
class MulLayer:
def __init__(self): #定义初始值
self.x = None
self.y = None
def forward(self, x, y): #前向传播,输入的x和y相乘
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout): #反向传播,导数
dx = dout * self.y #对于x的导数就是y
dy = dout * self.x #同上
return dx, dy
apple = 100
apple_num = 2
tax = 1.1
mul_apple_layer = MulLayer() #一个乘法计算苹果价钱
mul_tax_layer = MulLayer() #一个乘法计算税
#forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)
#backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice) #返回第一个节点的导数
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dTax:", dtax)
price: 220
dApple: 2.2
dApple_num: 110
dTax: 200
1.2 加法层的实现,AddLayer 并且实现例子
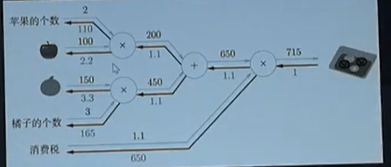
import numpy as np
class AddLayer:
def __init__(self):
pass #不需要特意初始化
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
#layer
mul_apple_layer = MulLayer() #四个节点,easy
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
#forward
apple_price = mul_apple_layer.forward(apple, apple_num)
orange_price = mul_orange_layer.forward(orange, orange_num)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)
price = mul_tax_layer.forward(all_price, tax)
#backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dOrange:", dorange)
print("dOrange_num:", int(dorange_num))
print("dTax:", dtax)
price: 715
dApple: 2.2
dApple_num: 110
dOrange: 3.3000000000000003
dOrange_num: 165
dTax: 650
2 激活函数层的实现
将计算图的思路应用到神经网络中,把构成神经网络的层实现为一个类。
先来实现激活函数的ReLU层和Sigmoid层。
2.1ReLU
若正向输入大于零,则反向输入将上游的值原封不动的传给下游。反过来,若小于零,则反向传播传给下游的信号留在此处。如下图所示:

import numpy as np
class Relu:
def __init__(self):
self.mask = None #实例变量mask;此变量由true/false组成的numpy数组
#把正向传输时的输入x元素小于0的保存为true,反之亦然。
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout*1
return dx
x = np.array([[0.1, -0.5],[-0.2, 0.3]])
print(x)
[[ 0.1 -0.5]
[-0.2 0.3]]
mask = (x <= 0)
print(mask)
[[False True]
[ True False]]
relu层和电路开关一样。正向传播,有电流,开关on;没电流,off。
反向传播,开关on,电流通过;off,不通过。
2.2 sigmoid函数层实现
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
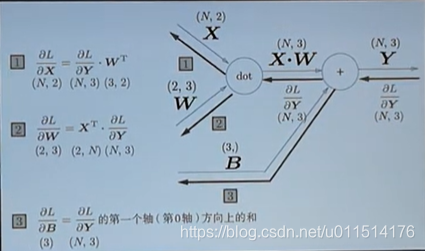
2.3 Affine/Softmax层的实现
#补充numpy数组广播原则,正向传播,偏置会加到每一个数据上
import numpy as np
X_dot_W = np.array([[0, 0, 0],[10, 10, 10]])
B = np.array([1, 2, 3])
X_dot_W
array([[ 0, 0, 0],
[10, 10, 10]])
X_dot_W + B
array([[ 1, 2, 3],
[11, 12, 13]])
实现Affine层
class Affine:
def __init__(self, W, b):
self.W =W
self.b = b
self.x = None
self.original_x_shape = None
# 权重和偏置参数的导数
self.dW = None
self.db = None
def forward(self, x):
# 对应张量
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)
return dx
#反方向传播,各个数据的反向传播的值要汇总为偏置的元素
dout = np.array([[1, 2, 3],[4, 5, 6]])
np.sum(dout, axis=0)
array([5, 7, 9])