一、问题
- 回归问题:得到一个或多个离散预测值
- 分类问题:得到一个或多个分类
二、分类
- 有监督学习:教计算机学习。有数据集,且已知正确答案,拿给机器训练,然后让机器在新问题中得到正确答案。
如:判断肿瘤是良性还是恶性,训练数据集中已经标注了那些是良性那些是恶性。还有反垃圾邮件。- 无监督学习:计算机自己学习。有数据集,但不知道正确答案(数据的结构)。如聚类分析,输入数据,得到多个簇。
如:谷歌新闻,基因分析,将基因数据分段(类),语音分离。
三、吴恩达老师推荐软件
- Octave:开源免费,写模型块,比Java, C++, Python快。也可用Matlab。
Octave和Matlab有内置的各种函数,一般先用Octave建立算法模型,并确定能用,再移植到C++和Java上。
四、模型描述
4.1 线性回归
符号:
m:训练样本的数量
x:输入变量或特征
y:输出变量或目标变量
(x, y):一组训练样本
( x ( i ) , y ( i ) x^{(i)},y^{(i)} x(i),y(i)):第i个训练样本
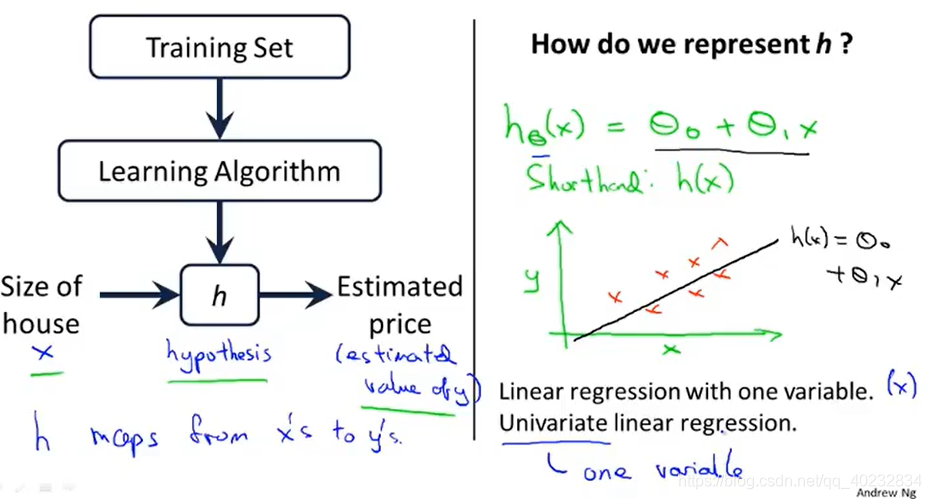
h:假设函数,是一个机器学习的术语。在线性回归里就是线性回归函数,其实就是把训练集通过学习算法,算出回归函数的 θ 0 \theta_0 θ0?和 θ 1 \theta_1 θ1?,从而得到回归函数,然后就可以通过输入参数得到预测值。
4.2 代价函数
在线性回归中,有
h
θ
=
θ
0
+
θ
1
x
h_\theta=\theta_0+\theta_1x
hθ?=θ0?+θ1?x,这是一元情况,多元情况为:
h
θ
=
θ
0
+
θ
1
x
+
+
θ
2
x
+
.
.
.
+
θ
p
x
h_\theta=\theta_0+\theta_1x++\theta_2x+...+\theta_px
hθ?=θ0?+θ1?x++θ2?x+...+θp?x。
那么怎么选择
θ
i
\theta_i
θi?,不同的
θ
i
\theta_i
θi?将得到不同的假设函数。
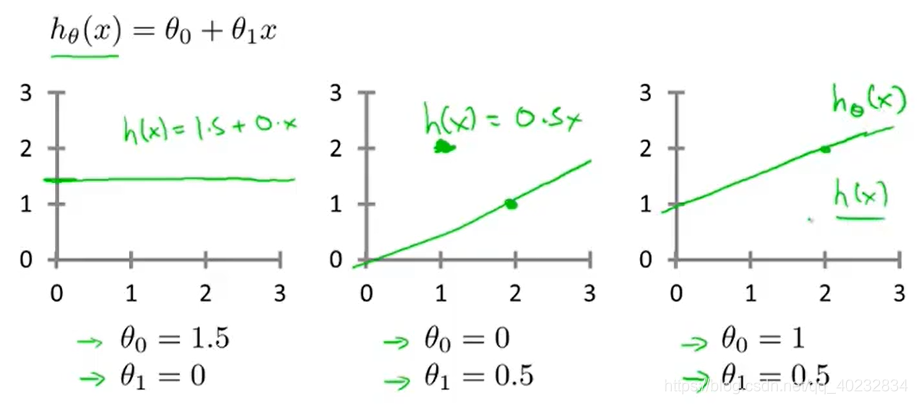

θ
i
\theta_i
θi?的选择就是使得
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})
2m1?∑i=1m?(hθ?(x(i))?y(i))取最小值。
J
(
θ
i
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
J(\theta_i)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})
J(θi?)=2m1?∑i=1m?(hθ?(x(i))?y(i))就是代价函数,也叫平方误差代价函数。这是解决回归问题最常用的代价函数。
x
(
i
)
,
y
(
i
)
x^{(i)},y^{(i)}
x(i),y(i)为训练集中的数据。

