[人工智能]你的模型又过拟合了？不如试试L1、L2正则

导读

因为L1正则化、L2正则化是为了缓解模型过拟合而提出的，所以在这之前，我们先说一说什么是过拟合以及欠拟合。

• 过拟合
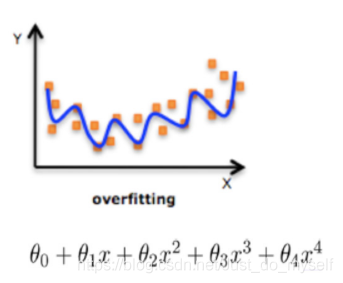
  在机器学习领域，模型基于数据训练的过程，其实是在学习训练数据的分布模式，在惩罚函数的约束下，它会尽可能地去记住训练数据集中的每一个样本点（即完整地学习到训练数据的分布）。我们拿线性回归举例，线性回归是要拟合一个函数，该函数需要尽可能地经过每个样本点，如图所示。但是众所周知，人为采集的数据集是不完美的，里边会包含缺失值、异常值等噪声，如果该函数将这些噪声也拟合了，这时候模型在训练数据上的损失很低，看上去很精确，可以识别大多部分的训练数据。但是由于噪声的干扰，模型其实是向错误的方向进行了演变，所以这时候模型的泛化性就不是很强，即给模型一个新的没见过的数据集，它的效果可能会非常差。这就是所谓的过拟合，即模型在训练过程中过度学习训练数据，然而训练数据有时不能代表数据的整体分布，所以模型对其他数据的效果变得较差，泛化性能不好。
  

• 欠拟合
  欠拟合，顾名思义，是与过拟合相反的。过拟合是模型过度拟合训练数据集，导致不能学习到真实的数据分布，泛化性能很差。那么欠拟合便是连训练数据都不能很好地进行拟合，就更不用谈泛化性能了。这时候原因多半是数据有问题，或者模型过于简单。我们看图说话，一目了然。
  
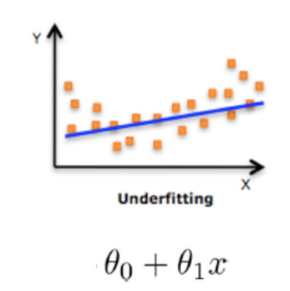
  说完了过拟合和欠拟合，也知晓了它们对模型性能带来的影响，那么有什么办法可以解决它们呢？下面看一下正则化手段。

正则化

正则化是机器学习中对原始的损失函数基础上引入额外信息，以防止过拟合和提升模型泛化性能的一类方法的统称。这里，常用的额外信息一般就是L1正则化和L2正则化，也叫做L1范数和L2范数。

L1正则化和L2正则化是损失函数里的额外惩罚项，就是就是对损失函数中的某些参数做一些限制，不让模型学习的过于复杂。对于我们上边举例的线性回归，线性回归 + L1 正则化 = Lasso回归，线性回归 + L2 正则化 = Ridge回归（岭回归）。其损失函数分别如下：

• 线性回归 + L1 正则化 = Lasso回归

• 线性回归 + L2 正则化 = Ridge回归（岭回归）

公式中ω是模型的参数，可以看到这两项正则化其实是对模型参数做了限制：

• L1正则化是指权值向量ω中各个元素的绝对值之和，通常表示 ||ω||1；
• L2正则化是指权值向量ω中各个元素的平方和然后再求平方根（我们可以看到Ridge回归的L2正则化项有平方符号），通常表示为 ||ω||2；
• 式中的λ是正则化对模型的限制程度，这个是认为调控的，即我们平时说的超参数，需要调参确定具体的值。

从式子(1) (2)可以看出，模型的训练目标是要最小化损失函数，如果我们在损失函数中加了L1正则化和L2正则化，那也就意味着，模型的参数也要尽可能的小(接近于0)，即稀疏化。简单说一下稀疏化，稀疏化说白了就是模型参数很多都为零，不起作用。通常在机器学习中，我们做分类任务，数据的特征维度是很高的，有可能是10K+级别，那么多特征，并不是所有的都对我们做分类有帮助，因此我们就希望模型在训练过程中能自动找到对其分类有帮助的那些特征，忽略不重要的特征(即该特征对应的权重接近于零甚至等于零)，这样一套组合拳打下来，模型只关注对应参数比较大的特征，忽略参数小的特征，相当于进行了一次自动的特征选择，提高模型的泛化能力，降低过拟合的风险。以上情况尤其针对样本数较小的情况。

L1正则化

前边说了正则化就是给损失函数加上约束项，从数学的角度来说就是给损失函数附加带约束条件，如式 (3) 所示。这样的话，问题就转变成了带约束条件的优化问题，立即推 ------>>>>>运用拉格朗日函数求解，如式 (4) 所示。


假设${\omega }_{?}$和${\lambda }_{?}$是上述优化问题的最优解，根据KKT条件，可以得到式子(5)。

我们知道L1正则化是参数的绝对值之和，接下来先讨论最简单的二维情况，即只有两个参数，那么L1正则化项L1_norm就等于|${\omega }_1$| + |${\omega }_2$|，将L1_norm在坐标系中画出来如图所示，图中也画出了原始损失函数(不带正则化约束项的)的等高线。

根据优化理论，我们知道当L1_norm与原始损失函数相等(即两函数曲线相交)的时候，取得最值。根据L1_norm的函数形状可知，它带有4个棱角，这两个函数曲线必在其中一个棱角处相交取最值，每个棱角处都会有一个参数(${\omega }_1$或${\omega }_2$)为零，进而推广到多维的情况，多维特征情况下，L1_norm会有很多个棱角，常识可知，向外凸出的棱角与外界物体接触的可能性大，而那些棱角上有很多参数为零，因此就造成了加上L1正则化之后会出现很多参数为零(稀疏化)的现象。以上就是为什么L1正则化为什么会产生稀疏化模型并进一步用于特征选择。

L2正则化

前边说完了L1正则化，同理，L2正则化只是约束条件的形式变了而已，由于L2正则化是平方和，所以它的函数图像画出来就是个圆形，如图所示。既然相比于L1正则化抹去了棱角，变得更加圆滑，那其与原始损失函数相交使得参数为零的概率就要变小好多，因此L2正则化不具备稀疏化的能力的原因。

L2正则化防止过拟合的原因

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是抗扰动能力强。

总结

这篇文章主要讲解了什么是过拟合以及欠拟合，以及正则化，又详细介绍了L1和L2正则化，并通过公式推导以及画图的形式生动地揭示了它们对模型进行稀疏化以及防止过拟合的内在原因。希望能够帮助到大家，谢谢浏览。如果有想法和疑问，欢迎大家评论区交流，觉得博主写的还行，对自己有帮助，可以给个赞呦。赠人玫瑰，手留余香~~