[人工智能]NLP-Task2:基于深度学习的文本分类

NLP-Task2:基于深度学习的文本分类

用Pytorch重写《任务一》，实现CNN、RNN的文本分类

数据集：Classify the sentiment of sentences from the Rotten Tomatoes dataset
网盘下载链接见文末（包括GloVe预训练模型参数）

• word embedding 的方式初始化

• 随机embedding的初始化方式

• 用glove 预训练的embedding进行初始化

• 知识点

  • CNN/RNN的特征抽取
  • 词嵌入
  • Dropout

本文参考：NLP-Beginner 任务二：基于深度学习的文本分类+pytorch(超详细！！)

一、介绍

1.1 要求

NLP任务：利用深度学习中的卷积神经网络（CNN）和循环神经网络（RNN）对文本的情感进行分类

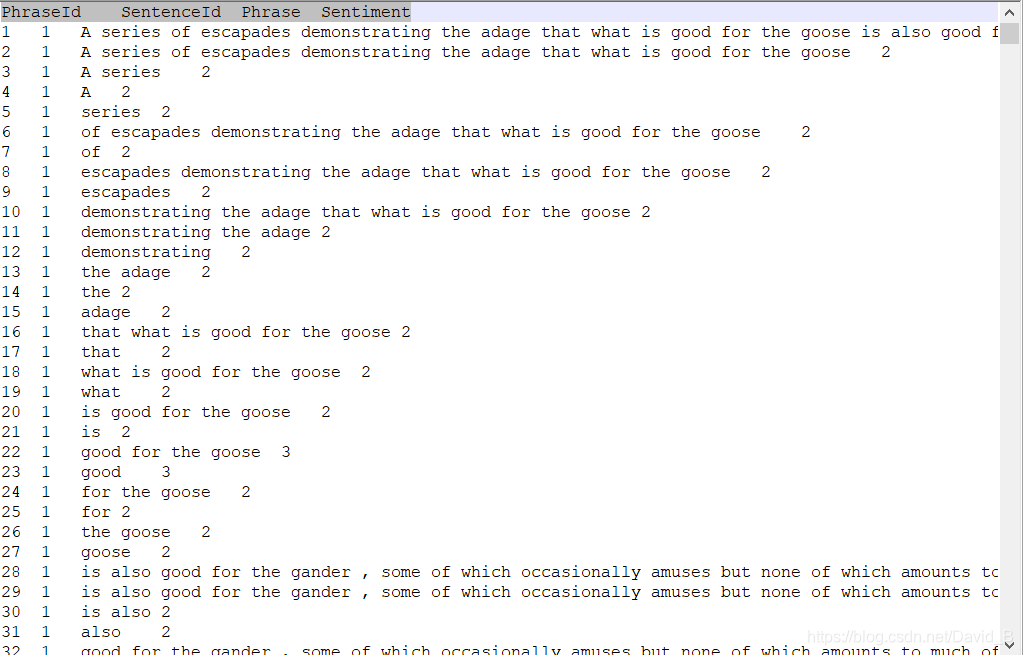
1.2 数据集

训练集共156060条英文评论，情感分共0-4类

二、特征提取—Word Embedding 词嵌入

2.1 词嵌入定义

把每一个词映射到一个高维空间，每个词代表一个高维空间的向量

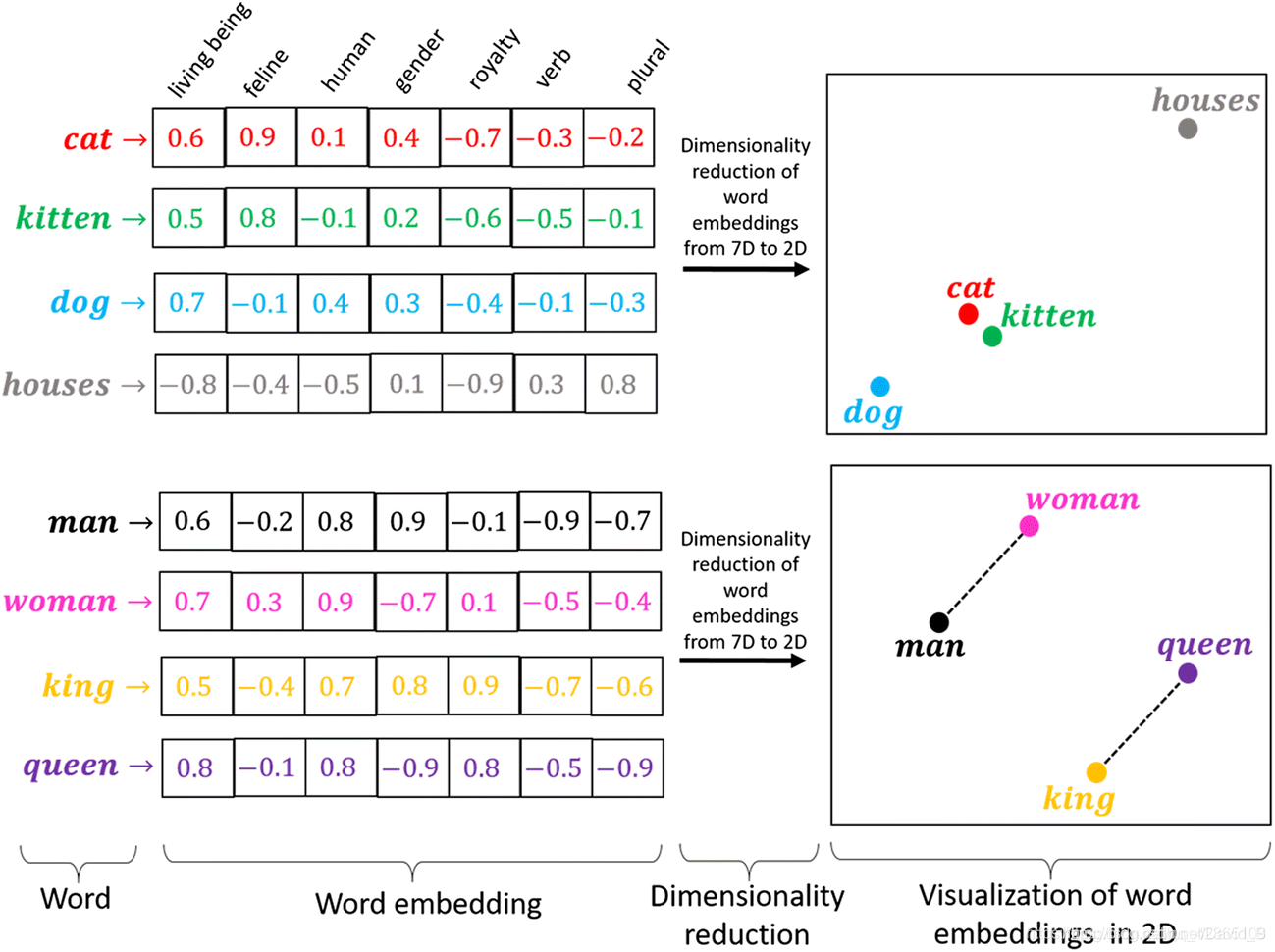
图中的例子是把每个单词映射到一个七维的空间

词嵌入模型优点：

• 当向量数值设计合理时，词向量与词向量之间的距离能体现出词与词之间的相似性
• 当向量数值设计合理时，词向量之间的距离也有一定的语义（如man–woman与king–queen）
• 可用较少的维数展现多角度特征

2.2 词嵌入的词向量

在词袋模型/N元特征中，只要设置好词和词组，就能把每一个句子（一堆词）转换成对应的0-1表示

但是在词嵌入模型中，并没有明确的转换规则，因此我们不可能提前知道每一个词对应的向量

上面的图的7维向量分别对应（living being, feline, human, gender, royalty, verb, plural），然而这只是为了方便理解所强行设计出的分类，很明显houses在gender维度的取值很难确定。因此，给每一个维度定义好分类标准，是不可能的

所以，在词嵌入模型中，我们选择不给每一个维度定义一个所谓的语义，我们只是单纯的把每一个词，对应到一个词向量上，我们不关心向量的数值大小代表什么意思，我们只关心这个数值设置得合不合理。换句话说，每个词向量都是参数，是待定的，需要求解，这点和词袋模型/N元特征是完全不同的。

2.3 词嵌入模型的初始化

词向量是一个参数，那么我们就要为它设置一个初始值，选取参数的初始值至关重要

如果选得好，就能求出一个更好的参数，甚至能起到加速模型优化的效果；初始值选的不好，那么优化模型求解的时候就会使参数值难以收敛，或者收敛到一个较差的极值

2.3.1 随机初始化

给定一个维度d，对每一个词$w$，随机生成一个d维的向量$x\in {\mathbb{R}}^d$

这种方法可能会生成交劣的初值，也没有良好的解释性

2.3.2 预训练模型初始化

使用别人训练好的模型作为初值，比如训练好的词嵌入模型GloVe

2.4 特征表示

给定每个词的词向量，即可将一个句子量化成一个ID列表，再转化成特征矩阵

设 d=5
（ID：1） I : \quad \quad [+0.10,+0.20,+0.30,+0.50,+1.50]
（ID：2） love : \quad [?1.00,?2.20,+3.40,+1.00,+0.00]
（ID：3） you : \quad [?3.12,?1.14,+5.14,+1.60,+7.00]
（ID：4） hate : \quad [?8.00,?6.40,+3.60,+2.00,+3.00]

句子 I love you便可表示为：[1,2,3]，经过词嵌入后得到
$$X=?\begin{array}{c}+0.10,+0.20,+0.30,+0.50,+1.50\\ ?1.00,?2.20,+3.40,+1.00,+0.00\\ ?3.12,?1.14,+5.14,+1.60,+7.00\end{array}?$$

句子 I hate you便可表示为：[1,4,3]，经过词嵌入后得到
$$X=?\begin{array}{c}+0.10,+0.20,+0.30,+0.50,+1.50\\ ?8.00,?6.40,+3.60,+2.00,+3.00\\ ?3.12,?1.14,+5.14,+1.60,+7.00\end{array}?$$

三、神经网络

3.1 卷积神经网络（Convolutional Neural Networks）

• 卷积层（convolution）
• 激活层（activation）
• 池化层（pooling）
• 全连接层（fully connected）

3.1.1 卷积层（convolution）

3.1.1.1 一维卷积

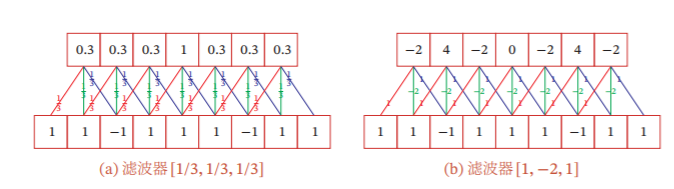
对于左图，待处理的向量 $x\in {\mathbb{R}}^n$ : $[1,1,?1,1,1,1,?1,1,1]$

卷积核 $w\in {\mathbb{R}}^k$:$[\frac{1}{3},\frac{1}{3},\frac{1}{3}]$

得到结果 $y\in {\mathbb{R}}^{n?k+1}$:$[\frac{1}{3},\frac{1}{3},\frac{1}{3},1,\frac{1}{3},\frac{1}{3},\frac{1}{3}]$

卷积操作记为：$y=w?x$

公式表示：$y_t=\sum _{k=1}^K{w}_k{x}_{t+k?1}(t=1,2,...,n?k+1)$

3.1.1.2 二维卷积

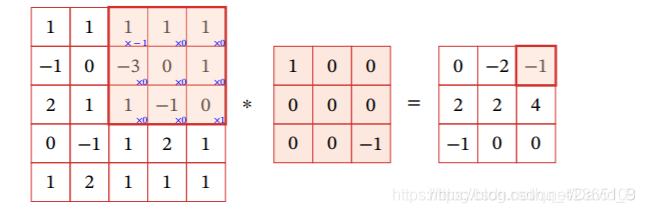
左一为待处理矩阵 $X\in {\mathbb{R}}^{n\times d}$

左二为卷积核 $W\in {\mathbb{R}}^{K_1\times K_2}$

得到右一矩阵 $Y\in {\mathbb{R}}^{(n?K_1+1)\times (d?K_2+1)}$

记为$Y=W?X$

公式表示：$Y_{ij}=\sum _{k_1=1}^{K_1}\sum _{k_2=1}^{K_2}{W}_{k_1,k_2}{x}_{i+k_1?1,j+k_2?1}$
${}^{(i=1,2,...,n?K_1+1,j=1,2,...,n?K_2+1)}$

3.1.1.3 卷积步长与零填充

上面例子的步长都是1，但步长也可以不为1

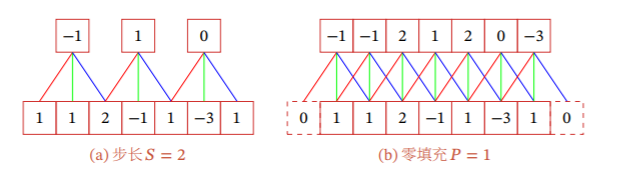
值得注意的是右图进行了零填充操作，可使待处理向量的边界元素能进行多次卷积操作，尽可能保留边界元素的特征

3.1.1.4 卷积层设计

卷积层的设计参考论文Convolutional Neural Networks for Sentence Classification

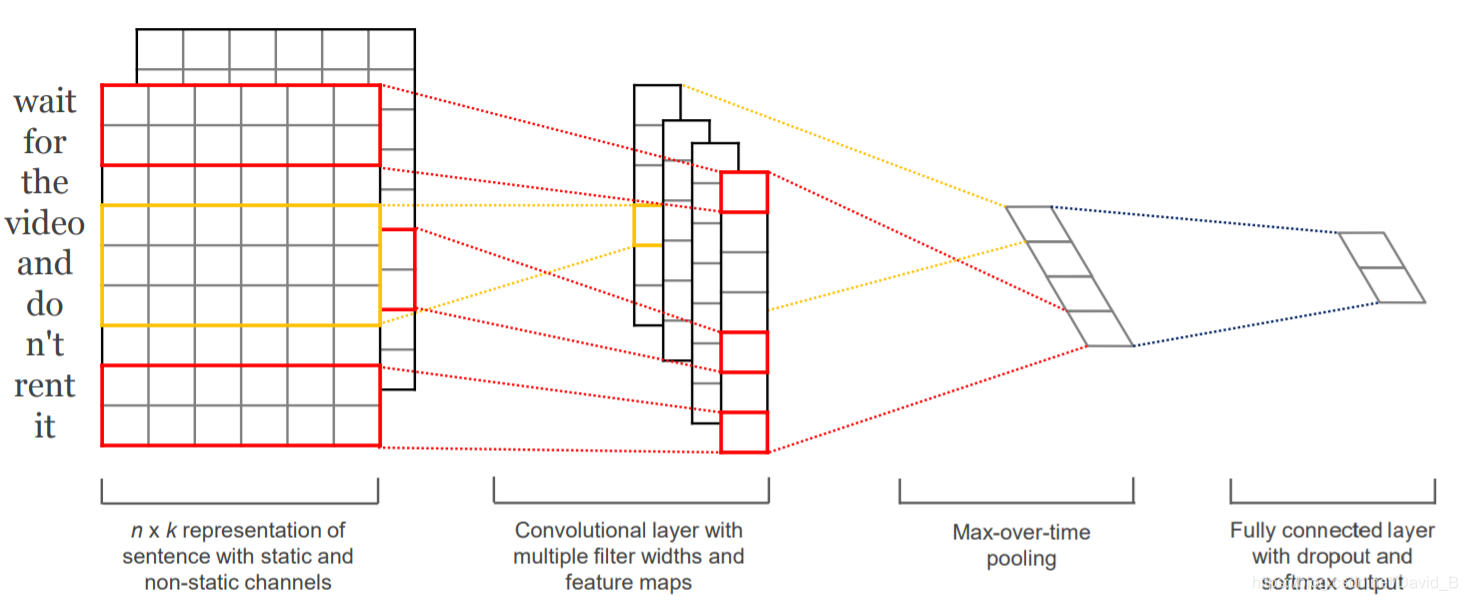
符合定义：$n$–句子长度；$d$–词向量长度；句子的特征矩阵 $X\in {\mathbb{R}}^{n\times d}$

本次任务中采用四种卷积核，大小分别为：$2\times d,3\times d,4\times d,5\times d$

$2\times d$的卷积核为上图红色框，$3\times d$为上图黄色框

例如：句子wait for的特征矩阵大小为 $2\times d$，经过卷积核 $2\times d$ 卷积后得到一个值

特征矩阵$X\in {\mathbb{R}}^{n\times d}$与卷积核$W\in {\mathbb{R}}^{2\times d}$卷积后，得到结果$Y\in {\mathbb{R}}^{(n?2+1)\times (d?d+1)}$

用四个卷积核的原因是为了挖掘词组的特征，如卷积核 $2\times d$ 挖掘两个单词之间关系，卷积核 $5\times d$ 挖掘五个单词之间关系

于是，对于一个句子，特征矩阵$X\in {\mathbb{R}}^{(n\times d)}$，经过四个卷积核$W$的卷积后，得到

$Y_1\in {\mathbb{R}}^{(n?1)\times 1}，Y_2\in {\mathbb{R}}^{(n?2)\times 1}，Y_3\in {\mathbb{R}}^{(n?3)\times 1}，Y_4\in {\mathbb{R}}^{(n?4)\times 1}$

以上介绍的是一个通道的情况，也可以设置多个通道，每个通道都像上述一样的操作，不过每一个通道的卷积核不一样，都是待定的参数，设置 $l$个通道，就会得到 $l$组$(Y_1,Y_2,Y_3,Y_4)$

3.1.2 激活层

在本次任务中，采用$ReLU$函数： $ReLU(x)=max(x,0)$

3.1.3 池化层（Pooling）

pooling有两种方法：最大池化及平均池化，详见《神经网络与深度学习》

本次任务中，用最大池化，对 $l$组$(Y_1,Y_2,Y_3,Y_4)$，对任意一组$(Y_1,Y_2,Y_3,Y_4)$里的任意一个向量$Y_i^{(l)}\in {\mathbb{R}}^{(n?i)\times 1}$，取其最大值，即（$Y_i^{(l)}(j)$表示第j个元素）

$y_i^{(i)}=ma{x}_j{Y}_i^{(l)}(j)$

经过最大池化后，得到$l$组 $(y_1,y_2,y_3,y_4)$

把它们按结果类别拼接起来，就可以得到一个长度为 $l?4$的向量

$Y=(y_1^1,...,y_1^l,y_2^1,...,y_2^l,y_3^1,...,y_3^l,y_4^1,...,y_4^l)$

3.1.4 全连接层（Fully connected）

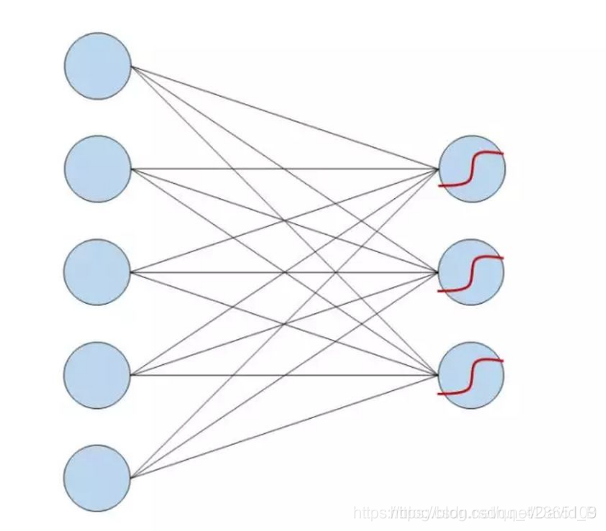
左边的神经元便是在最大池化后得到的向量（$l?4$）

而我们的目标是输出一个句子的情感类别，即输出也应该是属于五类情感的概率

$p=(0,0,0.7,0.25,0.05{)}^T$

因此在全连接层，我们把长度为$l?4$的向量转换成长度为5的向量

最简单的转换方式是线性变换 $p=AY+b$其中$A\in {\mathbb{R}}^{5\times (l?4)},Y\in {\mathbb{R}}^{(l?4)\times 1},A\in {\mathbb{R}}^{5\times 1}$

于是$A,b$便是待定的系数

3.1.5 总结

• 卷积层：特征矩阵$X?l$组$(Y_1,Y_2,Y_3,Y_4)$，神经网络参数：4$l$个卷积核$W$
• 激活层：$l$组$(Y_1,Y_2,Y_3,Y_4)?$$l$组$(Y_1,Y_2,Y_3,Y_4)$，无参数
• 池化层：$l$组$(Y_1,Y_2,Y_3,Y_4)?$$l$组$(y_1,y_2,y_3,y_4)$，无参数
• 全连接层：$Y?p$，神经网络参数：$A,b$

3.2 循环神经网络（RNN）

3.2.1 隐藏层（Hidden layer）

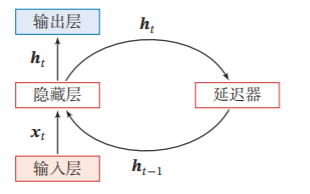
输入为特征矩阵$X$

（ID：1） I : \quad \quad [+0.10,+0.20,+0.30,+0.50,+1.50]
（ID：2） love : \quad [?1.00,?2.20,+3.40,+1.00,+0.00]
（ID：3） you : \quad [?3.12,?1.14,+5.14,+1.60,+7.00]

I love you便可表示为：

$$X=?\begin{array}{c}+0.10,+0.20,+0.30,+0.50,+1.50\\ ?1.00,?2.20,+3.40,+1.00,+0.00\\ ?3.12,?1.14,+5.14,+1.60,+7.00\end{array}?=[x_1,x_2,x_3{]}^T$$

在上述的CNN中，我们直接对矩阵$X$进行操作，而在RNN中，我们逐个对$x_i$进行操作

• 初始化$h_0\in {\mathbb{R}}^{l_h}$

• 计算以下两个公式，$t=1,2,..,n$

  • $z_t=U{h}_{t?1}+W{x}_t+b$，其中$U\in {\mathbb{R}}^{l_h\times l_h},W\in {\mathbb{R}}^{l_h\times d},z及b\in {\mathbb{R}}^{l_h}$
  • $h_t=f(z_t)$，$f(?)$是激活函数，本次任务中用$tanh$函数，$tanh(x)=\frac{exp(x)?exp(?x)}{exp(x)+exp(?x)}$

• 最后得到$h_n$

这一层的目的是把序列${x_i}_{i=1}^n$逐个输入到隐藏层中，得到的输出也会参与到下一次循环计算中，实现短期记忆功能

3.2.2 激活层

参照CNN

3.2.3 全连接层（Fully connected）

与CNN全连接层类似

3.2.4 总结

• 隐藏层：特征矩阵$X=[x_1,x_2,x_3{]}^T?h_n$，神经网络参数：$W,U,b_h$
• 全连接层：$h_n?p$，神经网络参数：$A,b_l$

3.3 训练神经网络

3.3.1 神经网络参数

先回顾CNN和RNN两个模型的参数：

• CNN：4$l$个卷积核$W$、$A,b$
• RNN：$W,U,b_h,A,b_l$

对任意一个网络，把参数记作 $\theta$

句子$x\text{Word?embedding}$特征矩阵$X$$\text{Neural?Network}$类别概率向量$p$

3.3.2 损失函数

在本次任务中使用交叉熵损失函数

给定一个神经网络NN，对于每一个样本n，其损失值为：

$L(N{N}_{\theta }(x^{(n)}),y^{(n)})=?\sum _{c=1}^C{y}_c^{(n)}log{p}_c^{(n)}=?(y^{(n)}{)}^{T}log{p}^{(n)}$

其中$y^{(n)}=(I(c=0),I(c=1),...,I(c=C))$是one-hot向量

对于N个样本，总的损失值是每个样本损失值的平均，即

$L(\theta )=L(N{N}_{\theta }(x),y)=\frac{1}{N}\sum _{n=1}^{N}L(N{N}_{\theta }(x^{(n)}),y^{(n)})$

通过找损失函数的最小值，求解最优的参数矩阵 $\theta$

3.3.3 最优参数求解—梯度下降法

公式：${\theta }_{t+1}\leftarrow {\theta }_t?\alpha \frac{?L({\theta }_t)}{?{\theta }_t}$

代码实现

4.1 实验设置

• 样本个数：约150000
• 训练集与测试集：7:3
• 模型CNN、RNN
• 初始化方法：随机初始化、GloVe预训练模型初始化
• 学习率：$10^{?3}$
• $l_h,d$：50
• $l$：最长句子的单词数
• Batch大小：500

4.2 代码

若不想用GPU加速，只需要把comparison_batch.py和Neural_Network_batch.py中所有的.cuda()和.cpu()删除，另外comparison_plot_batch.py中的.item()可能也要删除

数据处理

• 一批样本中句子长度不一可能需要进行零填充（padding），把同一个batch内的所有输入（句子）补充成一样的长度，但是若是句子之间长度差异过大（一句只有3个单词，一句有50个单词），就可能需要填充 多个无意义的0，会对性能造成影响，因此在本次任务中先把数据按句子长度进行排序，尽量使同一个batch内句子长度一致，避免零填充
• 加入Dropout层
  
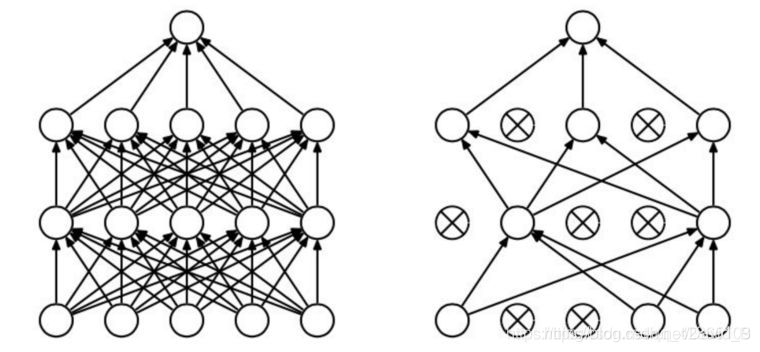
  代码

#特征提取feature_batch
import random
from torch.utils.data import Dataset, DataLoader
from torch.nn.utils.rnn import pad_sequence
import torch

def data_split(data, test_rate = 0.3):
    train = list()
    test = list()
    for sentence in data:
        if random.random() > test_rate:
            train.append(sentence)
        else:
            test.append(sentence)
            
    return train, test

class Random_embedding():
    #随机初始化
    def __init__(self, data, test_rate = 0.3):
        self.dict_words = dict()  #单词到ID的映射
        data.sort(key = lambda x: len(x[2].split())) #按照句子长度排序，短的在前
        self.data = data
        self.len_words = 0
        self.train, self.test = data_split(data, test_rate = test_rate)
        self.train_y = [int(term[3]) for term in self.train]
        self.test_y = [int(term[3]) for term in self.test]
        self.train_matrix = list()  #训练集的单词ID列表，叠成一个矩阵
        self.test_matrix = list()   #测试集的单词ID列表，叠成一个矩阵
        self.longest = 0   #记录最长的单词
        
    def get_words(self):
        for term in self.data:
            s = term[2]     #取句子
            s = s.upper()   #转为大写
            words = s.split()  #分成单词
            for word in words:
                if word not in self.dict_words:
                    self.dict_words[word] = len(self.dict_words) + 1 #padding是第0个，所以加一，第一个为0
        self.len_words = len(self.dict_words)  #单词数目
        
    def get_id(self):
        #训练集
        for term in self.train:
            s = term[2]
            s = s.upper()
            words = s.split()
            item = [self.dict_words[word] for word in words] #找到id列表（未进行padding）
            self.longest = max(self.longest, len(item))  #记录最长句子的单词数
            self.train_matrix.append(item)
        #测试集
        for term in self.test:
            s = term[2]
            s = s.upper()
            words = s.split()
            item = [self.dict_words[word] for word in words]
            self.longest = max(self.longest, len(item))
            self.test_matrix.append(item)
        self.len_words += 1   #单词数目（包括padding的ID：0）
        
class Glove_embedding():
    def __init__(self, data, trained_dict, test_rate = 0.3):
        self.dict_words = dict()  #单词到ID的映射
        self.trained_dict = trained_dict  #记录预训练词向量模型
        data.sort(key = lambda x: len(x[2].split()))
        self.data = data
        self.len_words = 0  #单词数目（包括padding的ID：0）
        self.train, self.test = data_split(data, test_rate = test_rate)
        self.train_y = [int(term[3]) for term in self.train]
        self.test_y = [int(term[3]) for term in self.test]
        self.train_matrix = list()  #训练集的单词ID列表，叠成一个矩阵
        self.test_matrix = list()   #测试集的单词ID列表，叠成一个矩阵
        self.longest = 0
        self.embedding = list()  #抽取出用到的（预训练模型的）单词
        
    def get_words(self):
        self.embedding.append([0] * 50)  #先填充词向量
        for term in self.data:
            s = term[2]  #取句子
            s = s.upper() #转大写
            words = s.split()
            for word in words:
                if word not in self.dict_words:
                    self.dict_words[word] = len(self.dict_words) + 1 #padding是第0个
                    if word in self.trained_dict:  #如果预训练模型有这个单词，直接记录词向量
                        self.embedding.append(self.trained_dict[word])
                    else:  #预训练模型中没有这个单词，初始化该单词对应的词向量为0向量
                        self.embedding.append([0] * 50)
        self.len_words = len(self.dict_words)  #单词数目（未包括padding的ID：0）
        
    def get_id(self):
        #train
        for term in self.train:
            s = term[2]
            s = s.upper()
            words = s.split()
            item = [self.dict_words[word] for word in words]  #找到id列表
            self.longest = max(self.longest, len(item))  #记录最长的单词
            self.train_matrix.append(item)
        for term in self.test:
            s = term[2]
            s = s.upper()
            words = s.split()
            item = [self.dict_words[word] for word in words]
            self.longest = max(self.longest, len(item))
            self.test_matrix.append(item)
        self.len_words += 1  #单词数目（未包括padding的ID：0）
        
class ClsDataset(Dataset):
    #自定义数据集的结构
    def __init__(self, sentence, emotion):
        self.sentence = sentence  #句子
        self.emotion = emotion    #情感
        
    def __getitem__(self, item):
        return self.sentence[item], self.emotion[item]
    
    def __len__(self):
        return len(self.emotion)
    
    
def collate_fn(batch_data):
    #自定义数据集的内数据返回方式，并进行padding
    sentence, emotion = zip(*batch_data)
    sentences = [torch.LongTensor(sent) for sent in sentence]  #把句子变成Longtensor类型
    padded_sents = pad_sequence(sentences, batch_first = True, padding_value = 0)  #自动padding操作
    return torch.LongTensor(padded_sents), torch.LongTensor(emotion)

def get_batch(x, y, batch_size):
    #利用dataloader划分batch
    dataset = ClsDataset(x, y)
    dataloader = DataLoader(dataset, batch_size = batch_size, shuffle = False, drop_last = True, collate_fn = collate_fn)
    #drop_last指不利用最后一个不完整的batch
    return dataloader

#神经网络---Neural_network_batch
import torch
import torch.nn as nn
import torch.nn.functional as F

class MY_RNN(nn.Module):
    def __init__(self, len_feature, len_hidden, len_words, typenum=5, weight=None, layer=1, nonlinearity='tanh',
                batch_first=True, drop_out=0.5):
        super(MY_RNN, self).__init__()
        self.len_feature = len_feature  #d的大小
        self.len_hidden = len_hidden  #l_h的大小
        self.len_words = len_words  #单词个数（包括padding）
        self.layer = layer  #隐藏层层数
        self.dropout = nn.Dropout(drop_out) #dropout层
        if weight is None:  #随机初始化
            x = nn.init.xavier_normal_(torch.Tensor(len_words, len_feature))  
            #xavier初始化方法中服从正态分布,通过网络层时，输入和输出的方差相同
            self.embedding = nn.Embedding(num_embeddings=len_words, embedding_dim=len_feature, _weight=x).cuda()
        else:  #GloVe初始化
            self.embedding = nn.Embedding(num_embeddings=len_words, embedding_dim=len_feature, _weight=weight).cuda()
        #用nn.Module的内置函数定义隐藏层
        self.rnn = nn.RNN(input_size=len_feature, hidden_size=len_hidden, num_layers=layer, nonlinearity=nonlinearity,
                         batch_first=batch_first, dropout=drop_out).cuda()
        
        #全连接层
        self.fc = nn.Linear(len_hidden, typenum).cuda()
        #冗余的softmax层可以不加
        #self.act = nn.Softmax(dim=1)
        
    def forward(self, x):
        #x:数据（维度为[batch_size, len(sentence)]）
        x = torch.LongTensor(x).cuda()
        batch_size = x.size(0)
        #经过词嵌入后，维度为[batch_size, len(sentence), d]
        out_put = self.embedding(x)  #词嵌入
        out_put = self.dropout(out_put)   #dropout层
        
        #另一种初始化h_0的方式
        #h_0 = torch.randn(self.layer, batch_size, self.len_hidden).cuda()
        #初始化h_0为0向量
        h0 = torch.autograd.Variable(torch.zeros(self.layer, batch_size, self.len_hidden)).cuda()
        #dropout后不变，经过隐藏层后，维度为[1, batch_size, l_h]
        _, hn = self.rnn(out_put, h0)  #隐藏层计算
        #经过全连接层后，维度为[1, batch_size, 5]
        out_put = self.fc(hn).squeeze(0)
        #挤掉第0维度，返回[batch_size, 5]的数据
        #out_put = self.act(out_put)    #softmax层可以不加
        return out_put
    
class MY_CNN(nn.Module):
    def __init__(self, len_feature, len_words, longest, typenum=5, weight=None, drop_out=0.5):
        super(MY_CNN, self).__init__()
        self.len_feature = len_feature  # d的大小
        self.len_words = len_words   #单词数目
        self.longest = longest   #最长句子单词数目
        self.dropout = nn.Dropout(drop_out)  #dropout层
        if weight is None:  #随机初始化
            x = nn.init.xavier_normal_(torch.Tensor(len_words, len_feature))
            self.embedding = nn.Embedding(num_embeddings=len_words, embedding_dim=len_feature, _weight=x).cuda()
        else:  #GloVe初始化
            self.embedding = nn.Embedding(num_embeddings=len_words, embedding_dim=len_feature, _weight=weight).cuda()
        #Conv2d参数详解：（输入通道数：1，输出通道数：l_l，卷积核大小：（行数，列数））
        #padding指往句子两侧加0
        #若X为1*50，当W=2*50时，没办法进行卷积操作，因此要在x的两侧加0，（padding=（1，0）变成3*50）
        self.conv1 = nn.Sequential(nn.Conv2d(1, longest, (2, len_feature), padding=(1, 0)), nn.ReLU()).cuda() #第一个卷积核+激活层
        self.conv2 = nn.Sequential(nn.Conv2d(1, longest, (3, len_feature), padding=(1, 0)), nn.ReLU()).cuda() #第二个卷积核+激活层
        self.conv3 = nn.Sequential(nn.Conv2d(1, longest, (4, len_feature), padding=(2, 0)), nn.ReLU()).cuda() #第三个卷积核+激活层
        self.conv4 = nn.Sequential(nn.Conv2d(1, longest, (5, len_feature), padding=(2, 0)), nn.ReLU()).cuda() #第四个卷积核+激活层
        #全连接层
        self.fc = nn.Linear(4*longest, typenum).cuda()
        #softmax层
        #self.act = nn.Softmax(dim=1)
        
    def forward(self, x):
        #x：数据，维度[batch_size, 句子长度]
        x = torch.LongTensor(x).cuda()
        #经过词嵌入后，维度为[batch_size, 1, 句子长度， d]
        out_put = self.embedding(x).view(x.shape[0], 1, x.shape[1], self.len_feature)  #词嵌入
        #dropout后不变，记为X
        out_put = self.dropout(out_put)  #dropout层
        
        #X经过2*d卷积后，维度为[batch_size, l_l, 句子长度+2-1， 1]
        #挤掉第三维度， [batch_size, l_l, 句子长度+2-1]记为 Y_1, (句子长度+2-1中的2是padding造成的行数扩张)
        conv1 = self.conv1(out_put).squeeze(3)  #第1个卷积
        
        #X经过3*d卷积后，维度为[batch_size, l_l, 句子长度+2-2， 1]
        #挤掉第三维度，记为Y_2
        conv2 = self.conv2(out_put).squeeze(3)  #第2个卷积
        
        #X经过4*d卷积后，维度为[batch_size, l_l, 句子长度+4-3， 1]
        #挤掉第三维度，记为Y_2
        conv3 = self.conv3(out_put).squeeze(3)  #第3个卷积
        
        #X经过3*d卷积后，维度为[batch_size, l_l, 句子长度+4-4， 1]
        #挤掉第三维度，记为Y_2
        conv4 = self.conv4(out_put).squeeze(3)  #第4个卷积
        
        #分别对（Y_1, Y_2, Y_3, Y_4）第第二维进行pooling
        #得到4个[batch_size, l_l, 1]向量
        pool1 = F.max_pool1d(conv1, conv1.shape[2])
        pool2 = F.max_pool1d(conv2, conv2.shape[2])
        pool3 = F.max_pool1d(conv3, conv3.shape[2])
        pool4 = F.max_pool1d(conv4, conv4.shape[2])
        
        #拼接得到[batch_size, l_l*4, 1]的向量
        #挤掉第二维为[batch_size, l_l*4]
        pool = torch.cat([pool1, pool2, pool3, pool4], 1).squeeze(2)  #拼接起来
        #经过全连接层后，维度为[batch_size, 5]
        out_put = self.fc(pool)  #全连接层
        #out_put = self.act(out_put)  #softmax层可以不加
        return out_put

#结果&作图---comparison_plot_batch.py
import matplotlib.pyplot as plt
from torch import optim

def NN_embedding(model, train, test, learning_rate, iter_times):
    #定义优化器（求参数）
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)
    #损失函数
    loss_fun = F.cross_entropy
    #损失值记录
    train_loss_record = list()
    test_loss_record = list()
    long_loss_record = list()
    #准确率记录
    train_record = list()
    test_record = list()
    long_record = list()
    #torch.autograd.set_detect_anomaly(True)
    #训练阶段
    for iteration in range(iter_times):
        model.train()  #进入非训练模式
        for i, batch in enumerate(train):
            x, y = batch  #取一个batch
            y = y.cuda()
            pred = model(x).cuda()  #计算输出
            optimizer.zero_grad()  #梯度初始化
            loss = loss_fun(pred, y).cuda() #损失值计算
            loss.backward()  #反向传播梯度
            optimizer.step()  #更新参数
            
        model.eval()  #进入测试模式
        #本轮正确率记录
        train_acc = list()
        test_acc = list()
        long_acc = list()
        length = 20
        #本轮损失值计算
        train_loss = 0
        test_loss = 0
        long_loss = 0
        for i, batch in enumerate(train):
            x, y = batch #取一个batch
            y = y.cuda()
            pred = model(x).cuda()  #计算输出
            loss = loss_fun(pred, y).cuda()  #损失值计算
            train_loss += loss.item()  #损失值累计
            _, y_pre = torch.max(pred, -1)
            #计算本次batch的准确率
            acc = torch.mean((torch.tensor(y_pre==y, dtype=torch.float)))
            train_acc.append(acc)
            
        for i, batch in enumerate(test):
            x, y = batch
            y = y.cuda()
            pred = model(x).cuda()  #计算输出
            loss = loss_fun(pred, y).cuda()  #损失值计算
            test_loss += loss.item()  #损失值累计
            _, y_pre = torch.max(pred, -1)
            #计算本次batch准确率
            acc = torch.mean((torch.tensor(y_pre==y, dtype=torch.float)))
            test_acc.append(acc)
            if (len(x[0])) > length: #长句子侦测
                long_acc.append(acc)
                long_loss += loss.item()
                
        trains_acc = sum(train_acc) / len(train_acc)
        tests_acc = sum(test_acc) / len(test_acc)
        longs_acc = sum(long_acc) / len(long_acc)
        
        train_loss_record.append(train_loss / len(train_acc))
        test_loss_record.append(test_loss / len(test_acc))
        long_loss_record.append(long_loss / len(long_acc))
        
        train_record.append(trains_acc.cpu())
        test_record.append(tests_acc.cpu())
        long_record.append(longs_acc.cpu())
        print('----------- Iteration', iteration +1, '-----------')
        print('Train loss:', train_loss / len(train_acc))
        print('Test loss:', test_loss / len(test_acc))
        print('Train accuracy:', trains_acc)
        print('Test accuracy:', tests_acc)
        print('Long sentence accuracy:', longs_acc)
        
    return train_loss_record, test_loss_record, long_loss_record, train_record, test_record, long_record

def NN_embedding_plot(random_embedding, glove_embedding, learning_rate, batch_size, iter_times):
    #获得训练集和测试集的batch
    train_random = get_batch(random_embedding.train_matrix,
                             random_embedding.train_y, batch_size)
    test_random = get_batch(random_embedding.test_matrix,
                            random_embedding.test_y, batch_size)
    train_glove = get_batch(glove_embedding.train_matrix,
                            glove_embedding.train_y, batch_size)
    test_glove = get_batch(glove_embedding.test_matrix,
                           glove_embedding.test_y, batch_size)
    
    #模型建立
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    random_rnn = MY_RNN(50, 50, random_embedding.len_words)
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    random_cnn = MY_CNN(50, random_embedding.len_words, random_embedding.longest)
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    glove_rnn = MY_RNN(50, 50, glove_embedding.len_words, weight=torch.tensor(glove_embedding.embedding, dtype=torch.float))
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    glove_cnn = MY_CNN(50, glove_embedding.len_words, glove_embedding.longest, weight=torch.tensor(glove_embedding.embedding, dtype=torch.float))
    #rnn+random
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    trl_ran_rnn, tel_ran_rnn, lol_ran_rnn, tra_ran_rnn, tes_ran_rnn, lon_ran_rnn =\
        NN_embedding(random_rnn, train_random, test_random, learning_rate, iter_times)
    
    #cnn+random
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    trl_ran_cnn, tel_ran_cnn, lol_ran_cnn, tra_ran_cnn, tes_ran_cnn, lon_ran_cnn =\
        NN_embedding(random_cnn, train_random, test_random, learning_rate, iter_times)
    
    #rnn+glove
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    trl_glo_rnn, tel_glo_rnn, lol_glo_rnn, tra_glo_rnn, tes_glo_rnn, lon_glo_rnn =\
        NN_embedding(glove_rnn, train_glove, test_glove, learning_rate, iter_times)
    
    #cnn+glove
    torch.manual_seed(2021)
    torch.cuda.manual_seed(2021)
    trl_glo_cnn, tel_glo_cnn, lol_glo_cnn, tra_glo_cnn, tes_glo_cnn, lon_glo_cnn =\
        NN_embedding(glove_cnn, train_glove, test_glove, learning_rate, iter_times)
    
    
    #画图
    x = list(range(1, iter_times+1))
    plt.subplot(2, 2, 1)
    plt.plot(x, trl_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, trl_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, trl_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, trl_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Train Loss')
    plt.xlabel('Iterations')
    plt.ylabel('Loss')
    
    plt.subplot(2, 2, 2)
    plt.plot(x, tel_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, tel_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, tel_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, tel_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Test Loss')
    plt.xlabel('Iterations')
    plt.ylabel('Loss')
    
    plt.subplot(2, 2, 3)
    plt.plot(x, tra_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, tra_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, tra_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, tra_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Train Accuracy')
    plt.xlabel('Iterations')
    plt.ylabel('Accuracy')
    plt.ylim(0, 1)
    
    plt.subplot(2, 2, 4)
    plt.plot(x, tes_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, tes_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, tes_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, tes_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Test Accuracy')
    plt.xlabel('Iterations')
    plt.ylabel('Accuracy')
    plt.ylim(0, 1)
    
    plt.tight_layout()
    fig = plt.gcf()
    fig.set_size_inches(8, 8, forward=True)
    plt.savefig('main_plot.jpg')
    plt.show()
   
    plt.subplot(2, 1, 1)
    plt.plot(x, lon_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, lon_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, lon_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, lon_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Long Sentence Accuracy')
    plt.xlabel('Iterations')
    plt.ylabel('Accuracy')
    plt.ylim(0, 1)
    
    plt.subplot(2, 1, 2)
    plt.plot(x, lol_ran_rnn, 'r--', label='RNN+random')
    plt.plot(x, lol_ran_cnn, 'g--', label='CNN+random')
    plt.plot(x, lol_glo_rnn, 'b--', label='RNN+glove')
    plt.plot(x, lol_glo_cnn, 'y--', label='CNN+glove')
    plt.legend()
    plt.legend(fontsize=10)
    plt.title('Long Sentence Loss')
    plt.xlabel('Iterations')
    plt.ylabel('Loss')

    plt.tight_layout()
    fig = plt.gcf()
    fig.set_size_inches(8, 8, forward=True)
    plt.savefig('sub_plot.jpg')
    plt.show()

import csv
import random
import torch

with open('/kaggle/input/task2train/train.tsv') as f:
    tsvreader = csv.reader(f, delimiter = '\t')
    temp = list(tsvreader)
    
with open('/kaggle/input/glove6b50dtxt/glove.6B.50d.txt', 'rb') as f:
    lines = f.readlines()
    
#用GloVe创建词典
trained_dict = dict()
n = len(lines)
for i in range(n):
    line = lines[i].split()  #将单词与参数分割，以数组形式存储
    trained_dict[line[0].decode('utf-8').upper()] = [float(line[j]) for j in range(1, 51)] 
    #每一句话的数组第一个为单词，与之对应的是参数数组
    
#初始化
iter_times = 50
alpha = 0.001

#程序开始
data = temp[1:]
batch_size = 500

#随机初始化
random.seed(2021)
random_embedding = Random_embedding(data = data)
random_embedding.get_words() #找到所有单词并标记ID
random_embedding.get_id()    #找到每个句子拥有的单词ID

#预训练模型初始化
random.seed(2021)
glove_embedding = Glove_embedding(data = data, trained_dict = trained_dict)
glove_embedding.get_words()  #找到所有单词并标记ID
glove_embedding.get_id()     #找到每个句子拥有的单词ID

NN_embedding_plot(random_embedding, glove_embedding, alpha, batch_size, iter_times)

4.3 结果

4.3.1 总体效果

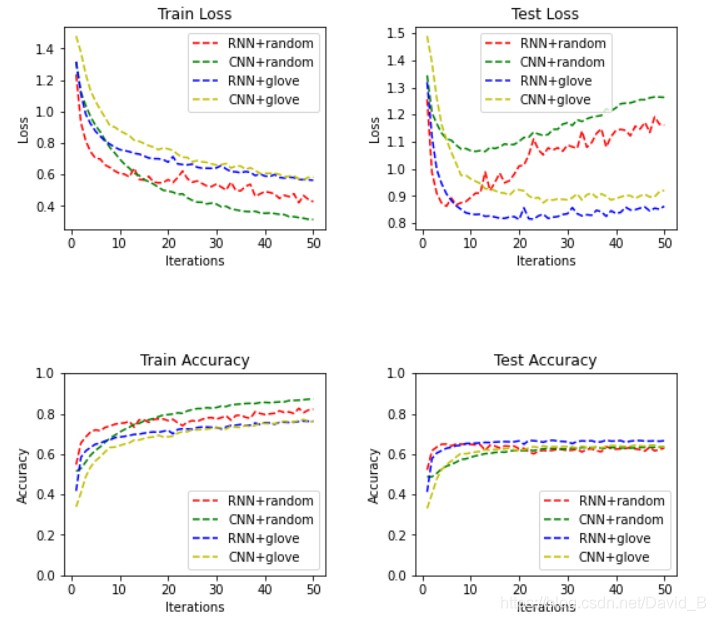
通过结果可以看出RNN比CNN的准确率在测试集和训练集上都要高

GloVe初始化比随机初始化效果更好一些

4.3.2 长句子分类效果

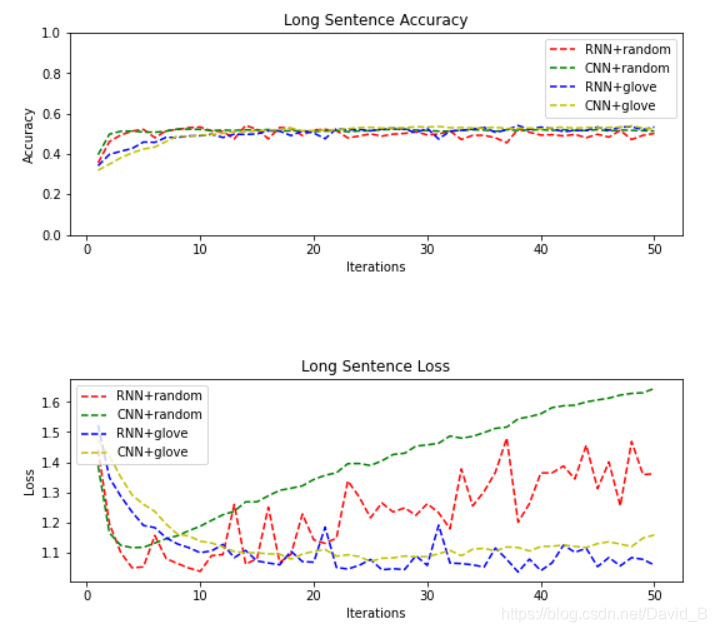
对于单词数大于20的句子，在本次任务中RNN与CNN的结果差别不是很大

其他

可以使用Kaggle的GPU跑代码

GloVe数据集
链接：https://pan.baidu.com/s/1OU4v-vXdKaNRZmkB6nWH-Q
提取码：gcmz