图预测任务实践
本文主要参考DataWhale图神经网络组队学习
图分类
例如预测化学分子的标签
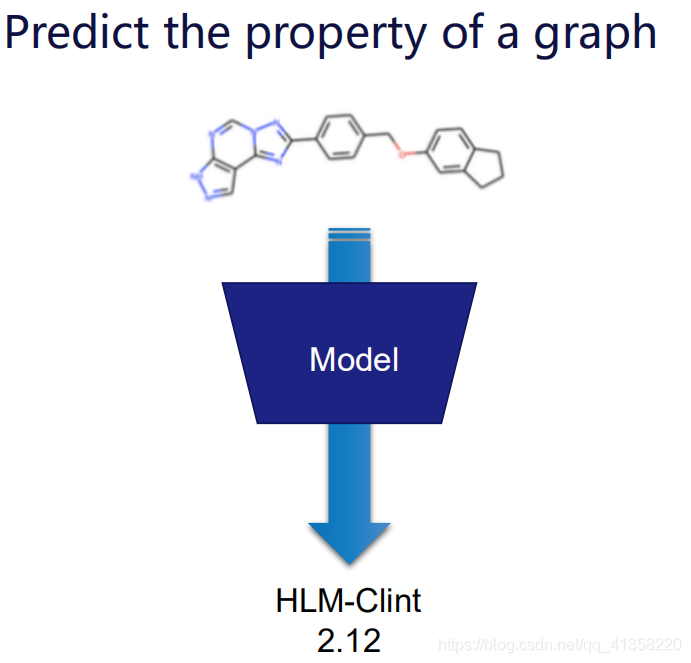
通过将获取到的节点表示经过池化得到图级别的表示,再利用图级别的表示进行损失函数的构造。
模型搭建
由于设备的关系,在对教程中的PCQM4M数据集处理存在一定问题,因此采用GIN模型对MUTAG数据集进行实验。
import os.path as osp
import torch
import torch.nn.functional as F
from torch.nn import Sequential, Linear, BatchNorm1d, ReLU
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_geometric.nn import GINConv, global_add_pool
path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', 'TU')
dataset = TUDataset(path, name='MUTAG').shuffle()
train_dataset = dataset[len(dataset) // 10:]
test_dataset = dataset[:len(dataset) // 10]
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128)
class Net(torch.nn.Module):
def __init__(self, in_channels, dim, out_channels):
super(Net, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(in_channels, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv2 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv3 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv4 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv5 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.lin1 = Linear(dim, dim)
self.lin2 = Linear(dim, out_channels)
def forward(self, x, edge_index, batch):
x = self.conv1(x, edge_index)
x = self.conv2(x, edge_index)
x = self.conv3(x, edge_index)
x = self.conv4(x, edge_index)
x = self.conv5(x, edge_index)
x = global_add_pool(x, batch)
x = self.lin1(x).relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return F.log_softmax(x, dim=-1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, 32, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
def train():
model.train()
total_loss = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data.x, data.edge_index, data.batch)
loss = F.nll_loss(output, data.y)
loss.backward()
optimizer.step()
total_loss += float(loss) * data.num_graphs
return total_loss / len(train_loader.dataset)
@torch.no_grad()
def test(loader):
model.eval()
total_correct = 0
for data in loader:
data = data.to(device)
out = model(data.x, data.edge_index, data.batch)
total_correct += int((out.argmax(-1) == data.y).sum())
return total_correct / len(loader.dataset)
for epoch in range(1, 101):
loss = train()
train_acc = test(train_loader)
test_acc = test(test_loader)
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, Train Acc: {train_acc:.4f} '
f'Test Acc: {test_acc:.4f}')
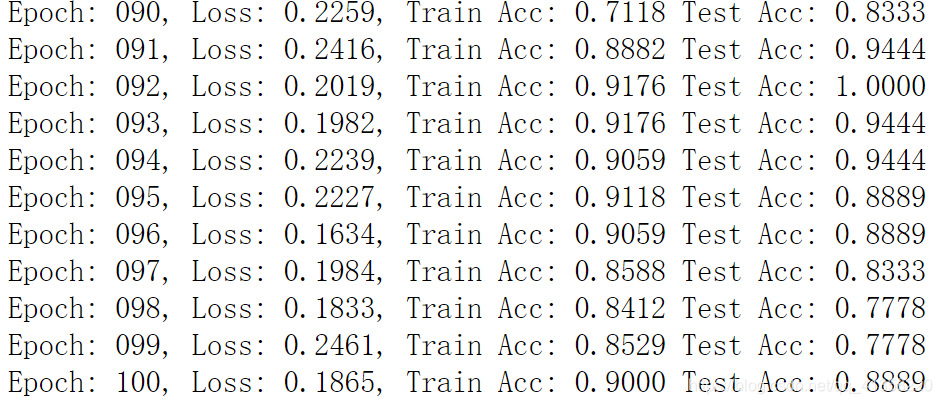
图分类结果如下所示:

调超参数进行实验结果对比
上述代码中设置了GIN的隐层维度为32,这里我们进行16和64的设置,查看实验结果对比:
import os.path as osp
import torch
import torch.nn.functional as F
from torch.nn import Sequential, Linear, BatchNorm1d, ReLU
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_geometric.nn import GINConv, global_add_pool
path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', 'TU')
dataset = TUDataset(path, name='MUTAG').shuffle()
train_dataset = dataset[len(dataset) // 10:]
test_dataset = dataset[:len(dataset) // 10]
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128)
class Net(torch.nn.Module):
def __init__(self, in_channels, dim, out_channels):
super(Net, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(in_channels, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv2 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv3 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv4 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv5 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.lin1 = Linear(dim, dim)
self.lin2 = Linear(dim, out_channels)
def forward(self, x, edge_index, batch):
x = self.conv1(x, edge_index)
x = self.conv2(x, edge_index)
x = self.conv3(x, edge_index)
x = self.conv4(x, edge_index)
x = self.conv5(x, edge_index)
x = global_add_pool(x, batch)
x = self.lin1(x).relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return F.log_softmax(x, dim=-1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, 16, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
def train():
model.train()
total_loss = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data.x, data.edge_index, data.batch)
loss = F.nll_loss(output, data.y)
loss.backward()
optimizer.step()
total_loss += float(loss) * data.num_graphs
return total_loss / len(train_loader.dataset)
@torch.no_grad()
def test(loader):
model.eval()
total_correct = 0
for data in loader:
data = data.to(device)
out = model(data.x, data.edge_index, data.batch)
total_correct += int((out.argmax(-1) == data.y).sum())
return total_correct / len(loader.dataset)
for epoch in range(1, 101):
loss = train()
train_acc = test(train_loader)
test_acc = test(test_loader)
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, Train Acc: {train_acc:.4f} '
f'Test Acc: {test_acc:.4f}')
将GIN隐层维度设置为16时,可以看到分类准确率明显提升。
import os.path as osp
import torch
import torch.nn.functional as F
from torch.nn import Sequential, Linear, BatchNorm1d, ReLU
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_geometric.nn import GINConv, global_add_pool
path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', 'TU')
dataset = TUDataset(path, name='MUTAG').shuffle()
train_dataset = dataset[len(dataset) // 10:]
test_dataset = dataset[:len(dataset) // 10]
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128)
class Net(torch.nn.Module):
def __init__(self, in_channels, dim, out_channels):
super(Net, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(in_channels, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv2 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv3 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv4 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.conv5 = GINConv(
Sequential(Linear(dim, dim), BatchNorm1d(dim), ReLU(),
Linear(dim, dim), ReLU()))
self.lin1 = Linear(dim, dim)
self.lin2 = Linear(dim, out_channels)
def forward(self, x, edge_index, batch):
x = self.conv1(x, edge_index)
x = self.conv2(x, edge_index)
x = self.conv3(x, edge_index)
x = self.conv4(x, edge_index)
x = self.conv5(x, edge_index)
x = global_add_pool(x, batch)
x = self.lin1(x).relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return F.log_softmax(x, dim=-1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, 64, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
def train():
model.train()
total_loss = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data.x, data.edge_index, data.batch)
loss = F.nll_loss(output, data.y)
loss.backward()
optimizer.step()
total_loss += float(loss) * data.num_graphs
return total_loss / len(train_loader.dataset)
@torch.no_grad()
def test(loader):
model.eval()
total_correct = 0
for data in loader:
data = data.to(device)
out = model(data.x, data.edge_index, data.batch)
total_correct += int((out.argmax(-1) == data.y).sum())
return total_correct / len(loader.dataset)
for epoch in range(1, 101):
loss = train()
train_acc = test(train_loader)
test_acc = test(test_loader)
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, Train Acc: {train_acc:.4f} '
f'Test Acc: {test_acc:.4f}')

如果将GIN隐层维度设置成64,会发现分类准确率大幅下降。
调学习率(lr)
隐层分别为16,32,64,将学习率由0.01设为0.05,查看实验结果对比。
16:

32:

64:

根据超参变化绘制准确率表
| dim | dim | dim | ||
|---|---|---|---|---|
| 16 | 32 | 64 | ||
| lr | 0.01 | 0.8889 | 0.7222 | 0.6111 |
| lr | 0.05 | 0.7222 | 0.5000 | 0.7222 |