问题描述:
神经网络:多变量反向传播求解问题py代码实现
神经网络要解决的经典问题就是黑盒测试猜数的过程:
- 通过输入值、输出值和期望值之间比较。
- 通过损失函数的计算误差值,误差值不理想
- 通过反向传播调整输入值。
- 反复此过程执行步骤1,直至损失函数误差值无限逼近期望误差结束。
例子,多变量反向传播:我们假设x=2a+3b,y=2b+1,z=x*y
那么当a和b为多少时,可以使期望值z=150?
解决方案:
我们先猜测a,b一个大致的值,使期望值接近150,设a=3,b=4.
- 当a=3,b=4,时,我们得到z=162.
- 损失函数我们设定为:delte_z=150-z
- 我们发现delte_z=-12,进行多变量反向传播调整a和b,利用sympy中diff函数求偏导,并计算delte_a,delte_b,通过反向传播调整a,b。
- 再次执行1-3步,循环5次,发现神奇的效果;
公式如下:
- 分别对a,b求偏导,带入a=3,b=4的值.
- 设置a和b的权重都是0.5.计算delte_a和delte_b
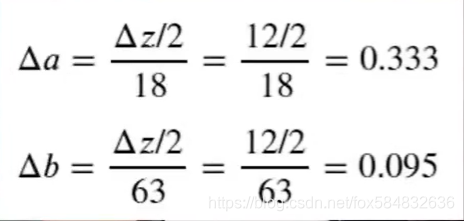
代码实现:
注意:
- 注意全局变量和函数局部变量
- 注意公式中符号问题
- 注意使用sympy时,对公式中参数赋值,先Symbol声明可替换字符,再diff求偏导,再subs赋值。
from sympy import *
# 求解x=2a+3b y=2b+1 z=x*y;输入a和b为3,4,期望z输出150
def xy_z(a, b):
x = 2 * a + 3 * b
y = 2 * b + 1
z = x * y
return z
def pd_xy(a1, b1, delta_z):
# 替换变量也可以写为x,y = symbols('x y')
a,b=0,0
a = Symbol('a') # 声明a是subs可替换的量
b = Symbol('b') # 声明b是subs可替换的量
z = (2 * a + 3 * b) * (2 * b + 1)
za = diff(z, a).subs(b, b1) # 对a求偏导
zb = diff(z, b).subs([(a, a1), (b, b1)]) # 对b求偏导
delta_a = delta_z * 0.5 / za
delta_b = delta_z * 0.5 / zb
print(delta_a,delta_b)
return delta_a, delta_b
a, b = 3, 4
delta_a, delta_b = 0,0
for i in range(5):
a = a + delta_a
b = b + delta_b
z = xy_z(a, b)
print(a,b)
print(z)
delta_z = 150 - z
delta_a, delta_b = pd_xy(a, b, delta_z)
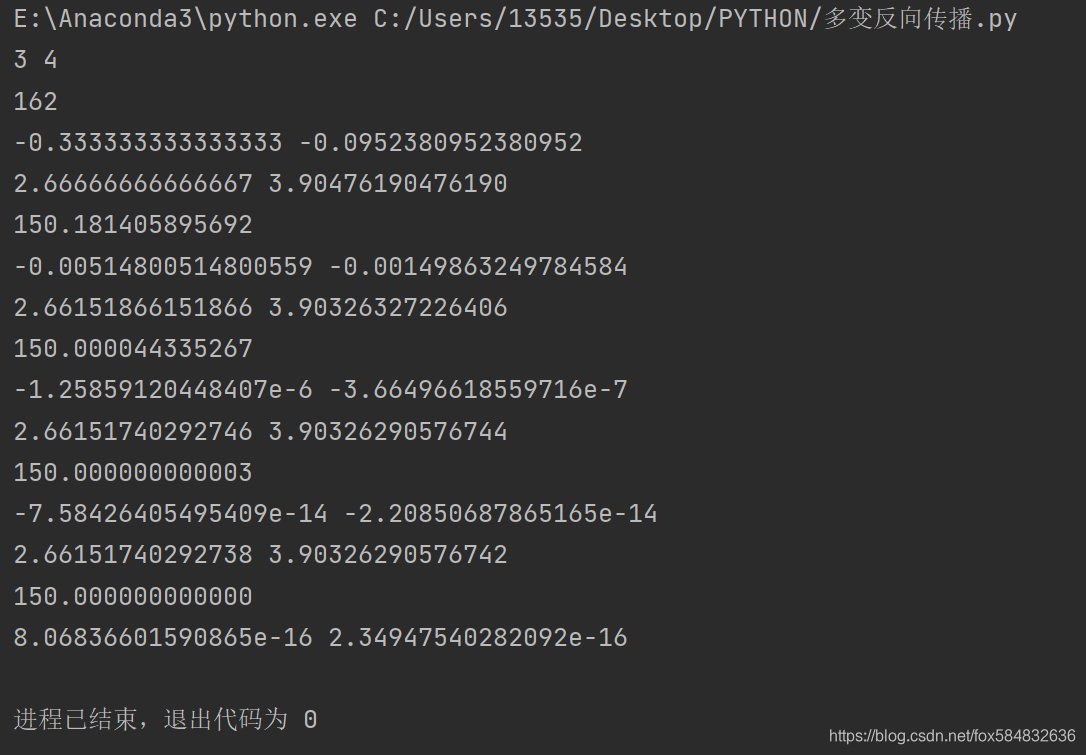
运行结果分析:
5次迭代已经找到合适的a和b的值。