文章目录
1 前馈神经网络及其产生动机
1.1 问题的产生
前馈神经网络(feedforward neural network)也称作深度前馈网络(deep feedforward network)或者多层感知机(multilayer perceptron MLP),是一种典型的机器学习模型。
回顾经典的机器学习模型,大致遵循以下步骤:
- 建立输入到输出的含参函数模型,往往选取一个宽泛抽象的函数族来满足多样性
- 建立损失函数来描述拟合结果与实际结果的差值
- 采用合适的优化方法优化你和函数的参数,使得损失函数最小化
- 在合适的迭代次数或者损失函数足够小并且拟合结果不至于欠拟合和过拟合时,我们认为学习结果可以接受
来到一个具体典型的例子,例如多元线性回归模型,我们使用矩阵w作为映射矩阵,向量b作为偏置向量来描述输入与输出的关系,使用拟合值和实际值的均方误差MSE作为损失函数,采用梯度下降(其实是一步到位了,没有下降的过程)进行优化。
可惜的是多元线性回归只能学习线性模型,我们没有办法表示输入变量之间的联系。
logistics回归其实就是无偏置的多元线性回归映射到sigmoid函数,用交叉熵cross entropy作为损失函数。
以上的机器学习方法都只使用了含少量参数的函数组去描述输入输出的映射关系,我们自然想到有没有一种工具可以成为一种万能的函数近似机,无论多么复杂多么非线性的函数都可以完成近似。
1.2 前馈神经网络的模型描述
前馈神经网络中,我们使用非线性的复合函数去完成函数拟合,像这样
f
(
x
)
=
f
(
3
)
(
f
(
2
)
(
f
(
1
)
(
x
)
)
)
(1.2.1)
f(x) = f^{(3)}(f^{(2)}(f^{(1)}(x))) \tag{1.2.1}
f(x)=f(3)(f(2)(f(1)(x)))(1.2.1)
用专业术语来讲,我们通常称
- f右上角的小标代表层数, f ( 3 ) f^{(3)} f(3)就是第三层
- 最大层数称为深度
- 每一层被定义为激活函数作用在线性映射上 f ( i ) ( x ) = σ ( w T x + b ) f^{(i)}(x)=\sigma(w^Tx+b) f(i)(x)=σ(wTx+b),激活函数有很多种可以选择,我们在后面会介绍
- 最开始是输入层,最终是输出层,中间的每一层成为隐藏层(因为训练数据并没有给出隐藏层的输入输出是多少,所以成为“隐藏”,但你是确切知道训练数据的每个输入对应什么输出的)
现在你可能会疑惑,包括为什么要这样定义每一层的映射,包括整个神经网络具体的函数递推式是怎样的,现在我希望从形象的角度阐述这个数学关系:
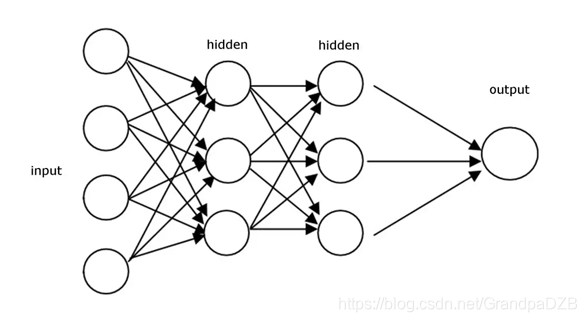
上图给出了一个神经网络的拓扑结构,我们首先考虑没有激活函数的情形,先看input层到hidden1层,可以发现每一层的每一个结点均由上一层的每一个结点作用(其实并不是所有的层都是这样,但这时最常见的一种层,叫做全连接层,在TensorFlow中成为Dense层),我们不妨设input的四个节点可以写成一个向量
x
x
x,hidden1层的三个结点的值分别是
h
1
h_1
h1?,
h
2
h_2
h2?,
h
3
h_3
h3?,那么有:
x
=
[
x
1
,
x
2
,
x
3
,
x
4
]
T
h
i
=
w
i
T
x
+
b
i
(1.2.2)
x=[x_1,x_2,x_3,x_4]^T \\ h_i=w^T_ix+b_i \tag{1.2.2}
x=[x1?,x2?,x3?,x4?]Thi?=wiT?x+bi?(1.2.2)
如此以来每一层到下一层结点的映射可以写成向量运算,层与层的关系可以写成矩阵运算,这实在是太酷了。在有些博客中你会发现示例图把每一个结点上都加了一个w,称作这个节点的权重,我个人不喜欢这个称呼,因为他就是为了表示一种线性映射而已。为什么用线性映射?没错,因为便于计算,足够简单,关系明确。
此时你应该就发现问题了,当每一层的映射都是线性映射的时候,显然输出关于输入也是线性的,依然无法表示非线性映射,因此我们对每一层的输出结果增加一个非线性的激活函数,变成这样:
h
i
=
σ
(
w
i
T
x
+
b
i
)
(1.2.3)
h_i=\sigma(w_i^Tx+b_i) \tag{1.2.3}
hi?=σ(wiT?x+bi?)(1.2.3)
激活函数有很多可以选择,例如很常见的sigmoid函数,后面会详细介绍。
线性函数嵌套非线性激活函数,再不断复合真的能够近似所有函数吗? 这是我当时最真实的疑惑。
前人给出了解答,万能近似定理(universal approximation theorem)(Hornik et al.,1989;Cybenko,1989)表明,一个前馈神经网络如果具有线性输出层和至少一层具有任何一种“挤压”性质的激活函数,例如sigmoid函数,的隐藏层,只要给予网络足够多数量的隐藏单元,他可以以任意的精度来近似任何一个有限维空间到另一个有限维空间的Borel可测函数。 可以放心的是现实生活没有实变函数那么糟心,几乎所有我们需要拟合的函数都是Borel可测的。
这里需要着重强调的是,激活函数的作用是为了给函数拟合网络添加非线性组成部分,某种程度上确实受到了神经科学的一点影响,但可以肯定的是神经网络的发展与生物神经科学以及人脑几乎没有什么关系,几乎完全依靠数学推动,神经网络的发展也并不是为了完成对人脑的近似,至少目前的研究方向是这样。如果了解了原理,那么到目前你应该能够发现它相对于之前的经典机器学习方法,只不过是一种能够对超级多参数(每一层就能产生那么多参数呢)进行优化拟合的万能函数近似器,本质上没有很大不同。
事实上万能近似定理没有那么棒,我们只知道可能无限逼近,却不知道无限逼近的代价是多大的算力。过多的层数可能引起过拟合,过少的层数可能引起欠拟合,越庞大的神经网络也需要越长的时间去优化,并且优化结束后你得到的是层层嵌套的复杂复合函数,极其不够直观,导致拟合结果缺乏很好的可解释性。
不可否认对于高度非线性的复杂函数,神经网络确实有大用,但是对于关系明确的简单数据集,我们宁愿使用支持向量机、逻辑回归、随机森林等方法获得更加快速高效的解。
现在我们了解了神经网络的拓扑结构与数学关系,那么还剩下一些遗留的细节问题
- 损失函数如何选择?
- 输出层如何选择?
- 激活函数如何选择?
- 如何进行优化?以及如此复杂的结构如何计算梯度?
2 损失函数的选择
大多数现代神经网络都会使用最大似然来进行训练,如果你对概率论的内容还有印象的话应该不难得到,对于给定的数据集data,关于参数
θ
\theta
θ的预测模型model应该使得数据集出现的概率最大,由于假定了数据的独立同分布,可以拆成独立的概率分布相乘,由于我们不喜欢相乘的形式,于是用ln函数拆分开:
L
(
θ
)
=
Π
p
m
o
d
e
l
(
y
∣
x
,
θ
)
l
n
L
(
θ
)
=
Σ
l
n
p
m
o
d
e
l
(
y
∣
x
,
θ
)
(2.0.1)
L(\theta)=\Pi p_{model}(y|x,\theta) \\ lnL(\theta) = \Sigma lnp_{model}(y|x,\theta) \tag{2.0.1}
L(θ)=Πpmodel?(y∣x,θ)lnL(θ)=Σlnpmodel?(y∣x,θ)(2.0.1)
为了使得似然函数最大,我们自然想到可以构造下面的损失函数,优化问题变成使损失函数最小:
J
(
θ
)
=
?
E
x
,
y
~
p
d
a
t
a
l
n
p
m
o
d
e
l
(
y
∣
x
,
θ
)
(2.0.2)
J(\theta)=-E_{x,y \sim p_{data}}ln p_{model}(y|x,\theta) \tag{2.0.2}
J(θ)=?Ex,y~pdata??lnpmodel?(y∣x,θ)(2.0.2)
这种方式非常的棒,因为一旦你确定了model的关系,就自然生成了一个损失函数。
2.1 均方误差(MSE)
我们考虑model是一个正态分布的情况:
p
m
o
d
e
l
(
y
∣
x
,
θ
)
=
N
(
y
;
f
(
x
∣
θ
)
,
I
)
=
e
x
p
(
?
1
2
(
y
?
f
(
x
∣
θ
)
)
T
I
(
y
?
f
(
x
∣
θ
)
)
)
(2.1.1)
p_{model}(y|x,\theta)=N(y;f(x|\theta),I)=exp(-\frac{1}{2}(y-f(x|\theta))^TI(y-f(x|\theta))) \tag{2.1.1}
pmodel?(y∣x,θ)=N(y;f(x∣θ),I)=exp(?21?(y?f(x∣θ))TI(y?f(x∣θ)))(2.1.1)
代入到式(2.0.2)中就可以得到:
J
(
θ
)
=
1
2
∣
∣
y
?
f
(
x
∣
θ
)
∣
∣
2
(2.1.2)
J(\theta)=\frac{1}{2}||y-f(x|\theta)||^2 \tag{2.1.2}
J(θ)=21?∣∣y?f(x∣θ)∣∣2(2.1.2)
这与优化均方误差是一样的!我依稀记得在推导多元正态分布的时候也是使用的正态分布+最大似然,效果和优化均方误差一致。
均方误差形式简单,是第一能想到的损失函数,但是问题在于神经网络的输出层往往包含一个指数项(又是sigmoid),会导致梯度过小(想想一下sigmoid的形状,在两端会有非常小的梯度),可以预见到这会严重影响梯度下降的速度。
2.2 交叉熵(cross entropy)
我们考虑model是一个多项分布的情况:
p
m
o
d
e
l
(
y
∣
x
,
θ
)
=
Π
f
(
x
∣
θ
)
p
y
~
d
a
t
a
(2.2.1)
p_{model}(y|x,\theta)=\Pi f(x|\theta)^{p_{y \sim data}} \tag{2.2.1}
pmodel?(y∣x,θ)=Πf(x∣θ)py~data?(2.2.1)
代入到式(2.0.2)中就可以得到:
J
(
θ
)
=
?
Σ
p
y
~
d
a
t
a
l
n
f
(
x
∣
θ
)
(2.2.2)
J(\theta)=-\Sigma p_{y\sim data}ln f(x|\theta) \tag{2.2.2}
J(θ)=?Σpy~data?lnf(x∣θ)(2.2.2)
或者简明一点:
J
(
θ
)
=
?
Σ
p
真
实
l
n
p
预
测
(2.2.3)
J(\theta)=-\Sigma p_{真实}ln p_{预测} \tag{2.2.3}
J(θ)=?Σp真实?lnp预测?(2.2.3)
你可能会突然发现这个结果和信息论里的交叉熵一致,从信息论的角度上来说,这正描述了预测结果与真实结果的一致性,同样具有很好的损失函数意义。用式(2.0.2)来引入这两种最常用的损失函数实在是非常美妙,它具有如此好的可解释性。最重要的是,交叉熵含有的对数项可以很好的解决预测结果含有的指数项,从而使得梯度大小回归正常,加快了优化速度,所以交叉熵也成为了最常使用的损失函数之一。
3 输出层的选择
(首先,这一部分在《深度学习》一书上占用了不小的篇幅,内容也几乎就是围绕着直接输出/二值输出/多项输出,书中从数学原理上给出了很深层的解读,说实话我再怎么仔细阅读也没有办法体悟除了功能性以外的东西 ,有需要的读者建议直接阅读原书籍)
3.1 Sigmoid输出单元
对于一个二分类问题,即输出结果我们只期望0或者1,我们希望拟合结果可以在输出层从实数域映射到[0,1]区间上,于是我们使用sigmoid函数作为输出层,这样的输出层显然是单个结点输出:
S
i
g
m
o
i
d
(
x
)
=
1
1
+
e
x
p
(
?
x
)
(3.1.1)
Sigmoid(x)=\frac{1}{1+exp(-x)} \tag{3.1.1}
Sigmoid(x)=1+exp(?x)1?(3.1.1)
3.2 Softmax输出单元
对于一个多分类问题,我们希望知道输出在众多可行分类中属于哪一种,那么期望结果应该类似于
y
=
[
0
,
?
?
,
1
,
?
?
,
0
]
y=[0,\cdots, 1, \cdots,0]
y=[0,?,1,?,0]这样,应该保证各分量和为1,且各个分量属于[0,1]区间,从具体意义上来讲也就是每个分量代表对应类别的概率。显然这样的输出结果是一个n维的向量。
S
o
f
t
m
a
x
k
(
x
)
=
e
x
p
(
x
k
)
∑
i
N
e
x
p
(
x
i
)
(3.2.1)
Softmax_k(x)=\frac{exp(x_k)}{ \sum_i^N exp(x_i)} \tag{3.2.1}
Softmaxk?(x)=∑iN?exp(xi?)exp(xk?)?(3.2.1)
4 激活函数的选择
4.1 整流线性单元及其拓展
整流线性单元(Rectified Linear Unit,Relu):
σ
(
z
)
=
m
a
x
{
0
,
z
}
\sigma(z)=max\{0,z\}
σ(z)=max{0,z}
由于它存在不可导点所以早期并不被看好,事实上Jarrett et al.(2009b)在文中提出在神经网络结构设计的几个不同因素中“使用整流非线性是提高识别系统性能的最重要的唯一因素”,Glorot et al. (2011a)从生物学角度提出生物神经元对于某些输入是完全不活跃的,整流线性单元可以很好的模仿这一点。同时对于大批量数据这种激活函数显然需要更小的运算量。
在TensorFlow中还提供了relu6函数,其实是relu的基础上再增加了最大值为6的限定。
渗漏整流线性单元(leaky ReLU,Maas et al. 2013) 提出将ReLU的0部分修改为斜率类似0.01的小值
参数化整流线性单元(parametric ReLU,PReLU,He et al. 2015) 提出把0部分的斜率作为学习参数
4.2 Sigmoid函数
sigmoid函数我们已经非常熟悉了,它具有在两端梯度非常小的缺点,会导致学习速度下降,当然这可以依靠选择适当的损失函数(对,就是交叉熵)来低效它的影响,但是显然依然不鼓励把它作为隐藏层的激活函数。
为什么不一直用整流线性单元呢?
对于循环神经网络以及自编码器等模型格外要求了不能使用分段函数,这时候只能使用sigmoid函数。
4.3 双曲正切tanh函数
双曲正切的表达式不是那么好记的,不过有简单的方法,我们设sigmoid函数为
σ
(
z
)
\sigma(z)
σ(z),则双曲正切可以表示为
t
a
n
h
(
z
)
=
2
σ
(
2
z
)
?
1
(4.3.1)
tanh(z)=2\sigma(2z)-1 \tag{4.3.1}
tanh(z)=2σ(2z)?1(4.3.1)
对于必须使用sigmoid的场合,双曲正切会有更好的表现效果。同时由于在z=0附近双曲正切类似于训练一个线性函数,他会使训练更加容易。
4.4 其他的激活函数
首先要说明的是,激活函数的作用依然是添加模型的非线性部分,他并不一定就是模仿神经元的刺激。ReLU激活函数确实看起来很像生物神经元的“激活”作用,但是有作者使用
h
=
c
o
s
(
w
T
x
+
b
)
h=cos(w^Tx+b)
h=cos(wTx+b)在MNIST上测试了前馈网络,获得了小于1%的误差率,这个结果很好,但这个激活函数却相当诡异,他的确和生物神经元没什么关系对吧。
更多的激活函数仍在被研究中,基本激活函数的改进通常都有略微的效果提升。
当然也有些效果不好的。
- 径向基函数(radical basis function, RBF) (Gaussian Kernal 也被成为径向基核,表达式都是exp(范数平方)的形式),它很难优化
- softplus函数,很容易想到这个函数就是ReLU的平滑版本,它是否能够融合ReLU和可导激活函数的优点?可惜Glorot et al. 2011a一文中比较了softplus和ReLU,发现后者其实效果更好,一般不鼓励使用softplus。
5 随机梯度下降与反向传播(BackPropagation)
目前我们所讨论的神经网络均是基于梯度下降的优化算法进行的,更多的优化算法(例如Adam)会在以后讨论。
梯度下降已经很熟悉了,可以预见对于超级大的样本量,和超级多参数的场合,一次迭代就需要计算样本量×参数量的梯度,这实在是太庞大,所以提出随机梯度下降的方式加快运算。
随机梯度下降(Stochastic parallel Gradient Descent algorithm, SGD) 它的想法非常简单,既然样本足够庞大,那么每次可以随机选取一部分的样本计算均值,作为整体梯度的无偏估计,这样每次只需要计算少量的梯度。
我相信你已经能够想到了,这并没有解决你最关心的问题——学习率怎样最优?这也将在以后讨论。
最后只剩下如何计算参数的梯度了,设损失函数为L,参数为w,那么问题就是求解
?
J
/
?
w
\partial J / \partial w
?J/?w,在反向传播出现以前这个问题非常困难,而反向传播简而言之就是复合函数求导链式法则罢了。

假设输出层表示为
y
=
g
(
x
)
=
f
(
3
)
(
f
(
2
)
(
f
(
1
)
(
x
)
)
)
y=g(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))
y=g(x)=f(3)(f(2)(f(1)(x))),那么损失函数可以表示为
L
(
y
)
L(y)
L(y),下面的等式均可以直接求出
?
L
/
?
y
=
L
y
′
y
=
f
(
3
)
(
w
2
T
h
1
+
b
)
?
y
/
?
w
2
=
(
?
f
(
3
)
/
?
w
2
)
h
1
?
?
L
/
?
w
2
=
(
?
L
/
?
y
)
(
?
y
/
?
w
2
)
=
L
y
′
(
?
f
(
3
)
/
?
w
2
)
h
1
(5.0.1)
\partial{L}/\partial{y}= L'_y \\ y=f^{(3)}(w_2^Th_1+b) \\ \partial{y}/\partial{w_2} = (\partial{f^{(3)}}/\partial{w_2})h_1 \\ \Rightarrow \partial{L}/\partial{w_2}=(\partial{L}/\partial{y})(\partial{y}/\partial{w_2})=L'_y (\partial{f^{(3)}}/\partial{w_2})h_1 \tag{5.0.1}
?L/?y=Ly′?y=f(3)(w2T?h1?+b)?y/?w2?=(?f(3)/?w2?)h1???L/?w2?=(?L/?y)(?y/?w2?)=Ly′?(?f(3)/?w2?)h1?(5.0.1)
按照上例的方法就可以用链式求导法则求出所有参数的梯度,因为是反向往回以此求解,所以称为反向传播。
至此我深感文字和公式的无力,不能直观形象简练地表述过程。推荐一个B站up主的视频手把手推导反向传播,短而简练,跟着算一遍就明白了。
如此以来我们已经可以利用上面的知识构建一个低效但可用的BP神经网络了,使用反向传播(BackPropagation)的前馈神经网络就称为BP神经网络。
相信我,它的具体实现过程十分繁琐,并且不像SVM等经典的机器学习算法,可以封装一个黑盒子,只需要给定输入、核函数形式、迭代次数,就可以直接得到结果。神经网络需要根据数据量和拟合情况自己设定合适的神经网络层数、节点数、拓扑结构等等。还好TensorFlow2.0给出了相当给力的搭建方法。
6 TensorFlow2.0的实现
(这并不是关于TensorFlow2.0的系统性说明,所以仅仅只会用到足以实现本文内容的一小部分,更多详情可以参考官方教程)
本文使用的数据集取自阿里天池关于classification的数据集——depression,数据集给出了被调查人员的许多生活情况资料,包括
年龄
已婚
人数_子女教育_水平
总_获得了成员(家庭)_资产
耐用_资产保存_资产
的生活_费用等_开支
传入_工资进入_自己的_农场进入_业务
进入的_任何_业务
传入_农业农场_开支
劳动_初级持久的_投资
没有_持久_调查
并包含被调查人员是否感到沮丧抑郁的布尔值。
首先不得不说的是按照我个人的先验经验,我并不觉得其中的某些参数会与人的沮丧情绪有很强的关联,如果真正要对这些数据进行分析的话,我可能会先用主成分分析进行数据降维提取关键信息,此外再进行数学上的归一化消除量纲影响。但是这都与本文无关了,我们就头铁拿这个数据硬分析!
(这个数据集有极个别数据存在确实现象,这可能导致numpy读取数据集出现无法直接转化成float类型的情况,因为存在空字符串)
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# 假设此时你已经完成了数据导入,存入data变量中
# 按照8:2的比例进行训练集与测试集的划分
N = data.shape[0]
dim = data.shape[1]
X_train = data[0:int(N*0.8), 0:-1]
X_test = data[int(N*0.8):, 0:-1]
Y_train = data[0:int(N*0.8), -1].reshape((1127,1))
Y_test = data[int(N*0.8):, -1].reshape((282,1))
这里我们使用Sequential建立神经网络模型,这种建立方式要求了神经网络应该只有单个输入单个输出(所谓的多个输入可以用一个向量,一个矩阵来表示,所以无所谓了),并且网络不应该有非线性的拓扑结构(这个问题也不会出现在我们这个简单的前馈神经网络里面)
调用layers的Dense方法可以创建一个全连接层,第一个参数是该层的结点数目,activation确定了该层使用的激活函数。
由于我们是在进行一个二分类问题,所以最后一层我选择了sigmoid函数作为输出,映射到(0,1)区间,其他各层均使用整流线性单元激活函数。
下面的代码可能会让你很懵,这么长一大串吗!没错,我尝试了较短的深度,结果是欠拟合,当不断增大参数量和深度的时候才慢慢出现了有概率过拟合的现象。为什么要这样设计深度和参数数量呢?我乱设置的,因为这个目前也没有很严谨的参考说明,理论上只要合适得复杂就可以。
请根据你的需要去设计网络的结构,当欠拟合时可以加深或者增加参数,或者增加迭代次数,当过拟合时反之。
# 建立神经网络模型
model = keras.Sequential(
[
#layers.InputLayer(input_shape=(22)),
layers.Dense(16, activation="relu"),
layers.Dense(32, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(512, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(32, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(1, activation='sigmoid'),
]
)
# 这一步并没有实际的意义,你可以认为就是指定了输入向量的规模并且应用的model
# y=model(x)
y = model(np.ones((1,22)))
model.compile()用于设置神经网络的具体参数,包括损失函数、优化器还有训练时实时输出的参考指标等等。你会在keras.losses后给出的自动展示中看到很多很多你熟悉的损失函数,仅仅是cross entropy就给出了三种,这里使用的是BinaryCrossentropy(),官方注释解释说这种损失函数是专门用于二分类问题的交叉熵,我也很好奇它和一般而言的交叉熵做了哪些改进。
优化方法同样有很多可以使用,但是结合本文粗浅的程度,我们这里暂时使用最简单粗暴的随机梯度下降法,也就是SGD()。
metrics指定了训练过程中实时输出的指标,这里设置为准确率,那么在训练过程中就能实时显示现在模型的预测准确度有多少,我们可以以此为依据判断模型效果。
在model.fit()中添加训练集就可以开始训练了。其中batch_size用于指定随机梯度下降时抽样的数量,正如你可以想象到的,这个数量如果过少,可能并不能很好地反映整体,导致很难收敛,这里我选择了200,默认是32。epochs指定了迭代次数,根据模型的拟合效果可以进行调整。
model.evaluate()用于检测测试集,可以体现拟合的泛化程度,我们总是希望泛化程度越高越好,如果你发现测试集的准确率显著低于训练集,那么显然是过拟合了,我们调整神经网络的结构就是为了在保证不过拟合的前提下,尽可能提高预测的准确率。
model.compile(
loss=keras.losses.BinaryCrossentropy(),
optimizer=keras.optimizers.SGD(),
metrics=['accuracy']
)
history = model.fit(X_train, Y_train, batch_size=200, epochs=230)
test_scores = model.evaluate(X_test, Y_test)
print(test_scores)
经过我自己的调整,最终模型可以在不过拟合的前提下最高达到87%左右的准确度,其实效果并不好,一方面我认为数据集不是很能反应人的沮丧状况,另一方面我也没有做预先的数据处理,除此之外我们使用的神经网络模型还是非常基础的模型,所以这个效果在意料之中我也可以接受。
起码对于这样子奇形怪状的参数,可能用其他传统的机器学习方法也很难做出好的结果了。
7 最后
写这篇文章的初衷是因为我容易忘记TensorFlow2.0的语法,csdn上相关的详细的资料也很少,我总不能每次都打开官方文档看一遍,不如自己写一份吧。但其实TensorFlow2.0实现部分是我最不喜欢的部分,机器学习的推动根本永远是依靠数学,从数学原理上理解这个运行流程是很酷的事情。
后面会继续跟进我的学习笔记,实现效果更好的神经网络。
正如你所见,我因如此简单的初衷胡吹出来的烂文章能得到如此高的评价让我倍感振奋。虽然我知道这个入选排名应该就是算法随便那么一排,实际上没有多少人会想看,但是还是倍感振奋。倍感振奋。