文章目录
- 1.1欢迎
- 1.2 什么是神经网络
- 1.3 用神经网络进行监督学习
- 1.4 为什么深度学习会兴起?
- 2.1 二分分类
- 2.2 logistic回归
- 2.3 logistic回归损失函数 logistic regression cost function
- 2.4 梯度下降法 gradient descent
- 2.5 导数
- 2.6 更多导数的例子
- 2.7计算图 computation graph
- 2.8 使用计算图求导
- 2.9 logistic回归中的梯度下降法
- 2.10 m个样本的梯度下降
- 2.11 向量化 vectorization
- 2.12 向量化的更多例子
- 2.13 向量化logistic回归
- 2.14 向量化logistic回归的梯度输出
- 2.15 python中的广播
- 2.16 python numpy向量的说明
- 2.17 Jupyter_ipython的快速指南
- 2.18 (选修)logistic损失函数的解释
- 3.1神经网络概览
- 3.2 神经网络表示
- 3.3 计算神经网络的输出
- 3.4 多个样本的向量化
- 3.5 向量化实现的解释
- 3.6激活函数
- 3.7 为什么需要激活函数?
- 3.8 激活函数的导数
- 3.9 神经网络的梯度下降法
- 3.10 直观理解反向传播
- 3.11 随机初始化
- 4.1 深层神经网络
- 4.2 前向和反向传播
- 4.3 深层网络中的前向传播
- 4.4 核对矩阵的维数
- 4.5 为什么使用深层表示
- 4.6 搭建深层网络神经块
- 4.7 参数VS超参数
- 4.8 这和大脑有什么关系?
1.1欢迎
1.2 什么是神经网络
最简单的神经网络
s
i
z
e
(
x
)
→
?
(
n
e
u
r
o
n
)
→
p
r
i
c
e
(
y
)
size(x)\rightarrow \bigcirc(neuron)\rightarrow price(y)
size(x)→?(neuron)→price(y)
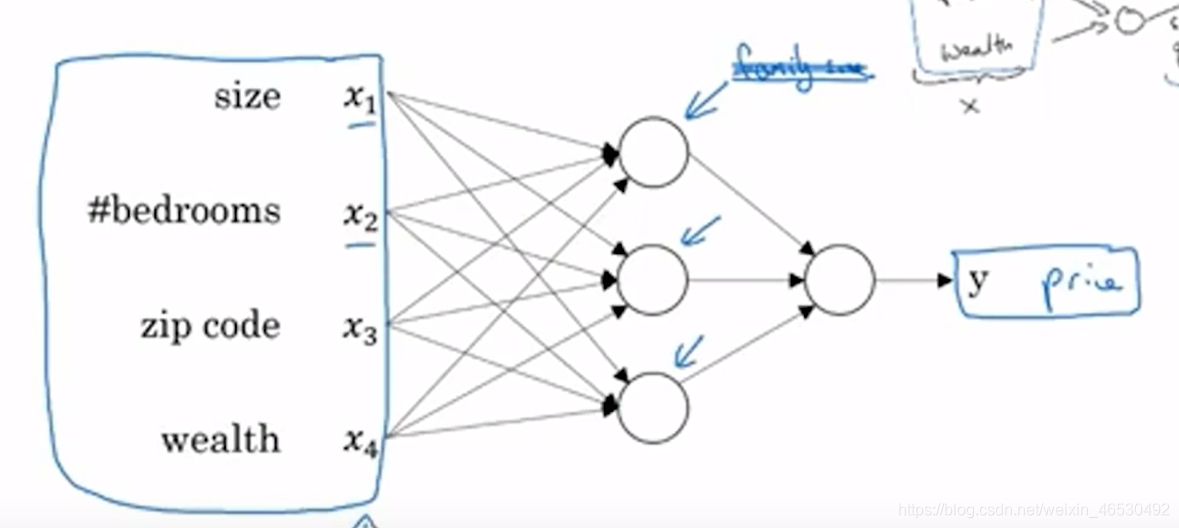
i
n
p
u
t
l
a
y
e
r
→
h
i
d
d
e
n
l
a
y
e
r
→
o
u
t
p
u
t
l
a
y
e
r
input \quad layer\rightarrow hidden\quad layer \rightarrow output \quad layer
inputlayer→hiddenlayer→outputlayer
1.3 用神经网络进行监督学习
CNN:适合于图像数据
RNN:适合(一维)时间序列数据
structured data结构化数据与unstructured data非结构化数据
1.4 为什么深度学习会兴起?
data(big data)
computer(CPU、GPU)
algorithms
好的算法的提升和计算机性能的改进都是为了计算速度的提升,使得程序可以在可接受的时间内完成。而大数据更大的作用在于得到结果的准确性的提升。
activation function激活函数
sigmoid函数:有部分区域梯度趋于0,参数变化会很慢,机器学习会很慢
ReLU函数:rectified linear unit 修正线性单元,可以解决上述问题
idea、code和experiment的循环
2.1 二分分类
logistic回归:二分分类算法
图片的矩阵表示:RGB通道
3
×
64
×
64
3\times64\times64
3×64×64参数
X
.
s
h
a
p
e
=
(
n
x
,
m
)
n
x
=
3
×
64
×
64
n
x
是
把
一
个
矩
阵
m
a
t
r
i
x
拉
平
f
l
a
t
t
e
n
X
=
(
x
(
1
)
,
x
(
2
)
,
…
…
x
(
m
)
)
Y
=
(
y
(
1
)
,
y
(
2
)
,
…
…
y
(
m
)
)
Y
.
s
h
a
p
e
=
(
1
,
m
)
X.shape = (nx,m)\\ nx =3\times64\times64\\ nx是把一个矩阵matrix拉平flatten\\ X = (x^{(1)},x^{(2)},……x^{(m)})\\ Y = (y^{(1)},y^{(2)},……y^{(m)})\\ Y.shape = (1,m)
X.shape=(nx,m)nx=3×64×64nx是把一个矩阵matrix拉平flattenX=(x(1),x(2),……x(m))Y=(y(1),y(2),……y(m))Y.shape=(1,m)
forward propagation正向传播
backward propagation反向传播
2.2 logistic回归
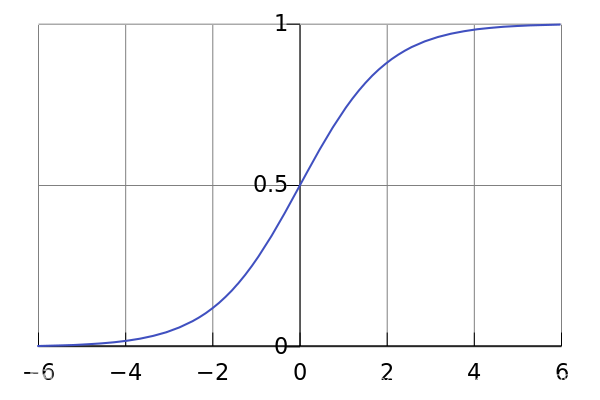
二分分类问题,所以希望输出值是介于0到1之间的值
g
i
v
e
n
x
,
w
a
n
t
y
^
=
P
(
y
=
1
∣
x
)
x
∈
R
n
x
p
a
r
a
m
e
t
e
r
s
:
w
∈
R
n
x
,
b
∈
R
o
u
t
p
u
t
:
y
^
=
σ
(
w
T
x
+
b
)
s
i
g
m
o
i
d
函
数
:
σ
(
z
)
=
1
1
+
e
?
z
given\quad x, want \quad \hat y = P(y=1|x)\\ x\in R^{nx}\\ parameters:w\in R^{nx},b\in R\\ output:\hat y =\textcolor{blue} \sigma(w^Tx+b)\\ sigmoid函数:\sigma(z) = \frac{1}{1+e^{-z}}
givenx,wanty^?=P(y=1∣x)x∈Rnxparameters:w∈Rnx,b∈Routput:y^?=σ(wTx+b)sigmoid函数:σ(z)=1+e?z1?
2.3 logistic回归损失函数 logistic regression cost function
loss function/error function: L ( y ^ , y ) = ? [ ( y l o g y ^ ) + ( 1 ? y ) l o g ( 1 ? y ^ ) ] L(\hat y,y)=-[(ylog\hat y)+(1-y)log(1-\hat y)] L(y^?,y)=?[(ylogy^?)+(1?y)log(1?y^?)]
损失函数应用于单个样本,成本函数是所有样本的总和。
c o s t f u n c t i o n : J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) cost \quad function:J(w,b) = \frac{1}{m}\sum_{i=1}^{m}L(\hat y^{(i)},y^{(i)}) costfunction:J(w,b)=m1?∑i=1m?L(y^?(i),y(i))
表示的是1到m项损失函数的平均
2.4 梯度下降法 gradient descent
KaTeX parse error: Undefined control sequence: \part at position 81: …w-\alpha \frac{\?p?a?r?t? ?J(w,b)}{\part w…
2.5 导数
2.6 更多导数的例子
2.7计算图 computation graph
2.8 使用计算图求导
链式求导法则
2.9 logistic回归中的梯度下降法
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PmoTCKpQ-1625930799955)(../AppData/Roaming/Typora/typora-user-images/image-20210709112838403.png)]](https://img-blog.csdnimg.cn/20210710233319343.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NjUzMDQ5Mg==,size_16,color_FFFFFF,t_70)
2.10 m个样本的梯度下降

2.11 向量化 vectorization
2.12 向量化的更多例子
python的numpy库
np.dot() np.exp() np.log() np.zeros() np.abs() np.maximum()
2.13 向量化logistic回归
numpy的广播函数 broadcasting
import numpy as np
z = np.dot(w.T,X)+b #向量加实数b,b会自动扩展成一个一维向量
2.14 向量化logistic回归的梯度输出
Z = w T X + b = n p . d o t ( w . T , X ) + b A = σ ( Z ) d Z = A ? Y d w = 1 m X d Z T d b = 1 m n p . s u m ( d Z ) w : = w ? α d w b : = b ? α d b Z = w^TX+b=np.dot(w.T,X)+b\\ A = \sigma(Z)\\dZ = A-Y\\ dw = \frac{1}{m}XdZ^T\\ db = \frac{1}{m}np.sum(dZ)\\ w:=w-\alpha dw\\ b:=b-\alpha db Z=wTX+b=np.dot(w.T,X)+bA=σ(Z)dZ=A?Ydw=m1?XdZTdb=m1?np.sum(dZ)w:=w?αdwb:=b?αdb
2.15 python中的广播
2.16 python numpy向量的说明
a = np.random.randn(5)
a
array([-1.29892536, 0.63302139, 1.49281709, 0.90560309, 1.3649011 ])
a,shape
(5,)
a.reshape(5,1)
array([[-1.29892536],
[ 0.63302139],
[ 1.49281709],
[ 0.90560309],
[ 1.3649011 ]])
b = np.random.randn(5,1)
b
array([[-0.50337928],
[ 0.34076192],
[ 0.16021539],
[ 0.4894436 ],
[ 0.4527971 ]])
b.shape
(5,1)
2.17 Jupyter_ipython的快速指南
shift+Enter 运行一段代码
cell run cell把文本语言变正常
2.18 (选修)logistic损失函数的解释
i f y = 1 : p ( y ∣ x ) = y ^ i f y = 0 : p ( y ∣ x ) = 1 ? y ^ s o p ( y ∣ x ) = y ^ y ( 1 ? y ^ ) 1 ? y l o g p ( y ∣ x ) = y l o g y ^ + ( 1 ? y ) l o g ( 1 ? y ^ ) = ? L ( y ^ , y ) if\quad y=1:p(y|x) = \hat y\\ if\quad y=0:p(y|x) = 1-\hat y\\ so \quad p(y|x) = \hat y^y(1-\hat y)^{1-y}\\ log p(y|x) = ylog\hat y+(1-y)log(1-\hat y) = -L(\hat y,y) ify=1:p(y∣x)=y^?ify=0:p(y∣x)=1?y^?sop(y∣x)=y^?y(1?y^?)1?ylogp(y∣x)=ylogy^?+(1?y)log(1?y^?)=?L(y^?,y)
最小化损失函数就是最大化
l
o
g
P
(
y
∣
x
)
(
i
.
i
.
d
)
logP(y|x)\quad(i.i.d)
logP(y∣x)(i.i.d)
p
(
l
a
b
e
l
s
i
n
t
a
r
g
e
t
s
e
t
)
=
∏
i
=
1
m
p
(
y
(
i
)
∣
x
(
i
)
)
l
o
g
p
(
l
a
b
e
l
s
i
n
t
a
r
g
e
t
s
e
t
)
=
l
o
g
∏
i
=
1
m
p
(
y
(
i
)
∣
x
(
i
)
)
=
∑
i
=
1
m
l
o
g
p
(
y
(
i
)
∣
x
(
i
)
)
=
?
∑
i
=
1
m
L
(
y
^
(
i
)
,
y
(
i
)
)
p(labels\quad in \quad target \quad set) = \prod_{i=1}^{m}p(y^{(i)}|x^{(i)})\\ log\quad p(labels\quad in \quad target \quad set) = log \quad\prod_{i=1}^{m}p(y^{(i)}|x^{(i)})\\=\sum_{i=1}^{m} log \quad p(y^{(i)}|x^{(i)})=- \sum_{i=1}^m L(\hat y^{(i)},y^{(i)})
p(labelsintargetset)=i=1∏m?p(y(i)∣x(i))logp(labelsintargetset)=logi=1∏m?p(y(i)∣x(i))=i=1∑m?logp(y(i)∣x(i))=?i=1∑m?L(y^?(i),y(i))
最大似然估计maximum likelihood function
c
o
s
t
:
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
(
i
)
,
y
(
i
)
)
cost:J(w,b) = \frac{1}{m}\sum_{i=1}^m L(\hat y^{(i)},y^{(i)})
cost:J(w,b)=m1?i=1∑m?L(y^?(i),y(i))
3.1神经网络概览
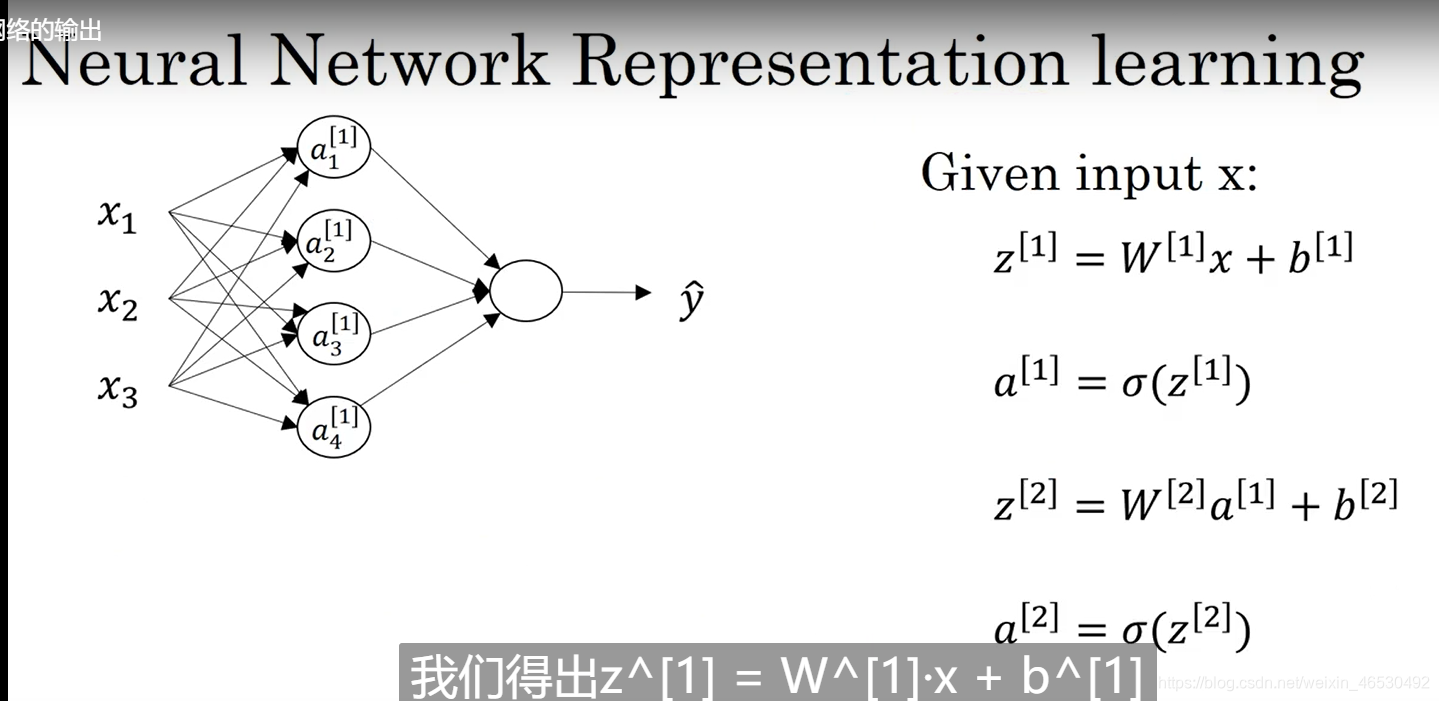
3.2 神经网络表示
一般标准的话不把输入层input layer看做标准的层
所以一个三层神经网络一般叫做标准的双层神经网络
3.3 计算神经网络的输出
[] : 方括号代表同一样本的不同层layer
():圆括号代表不同样本的同一层layer
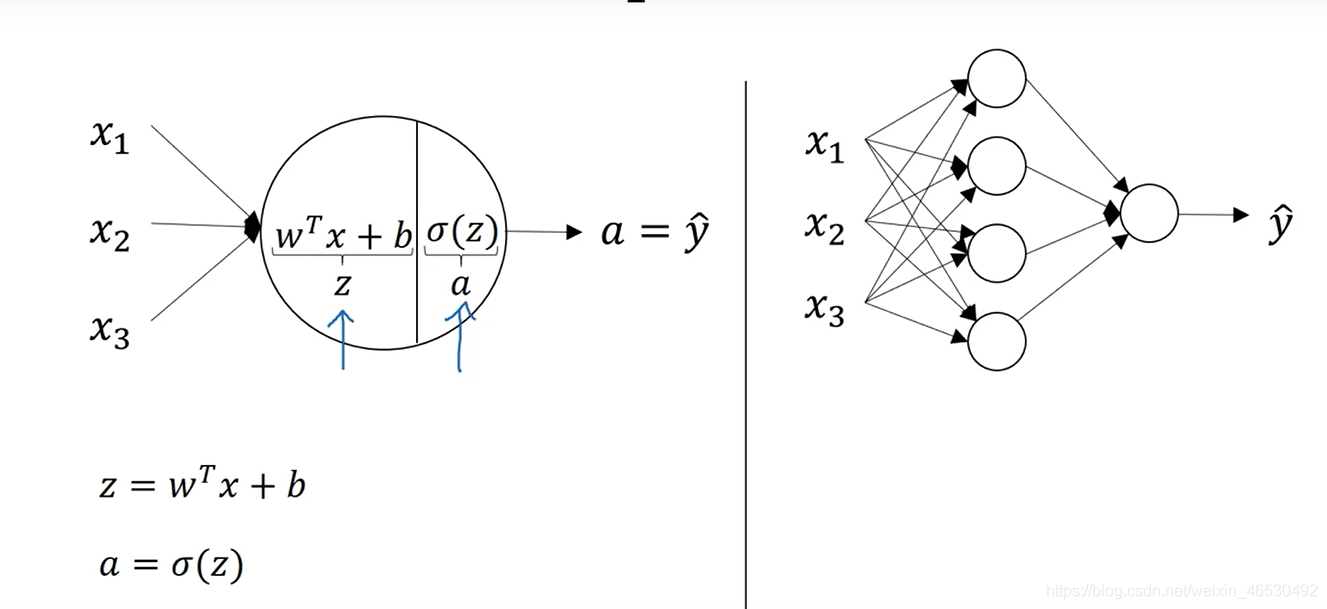
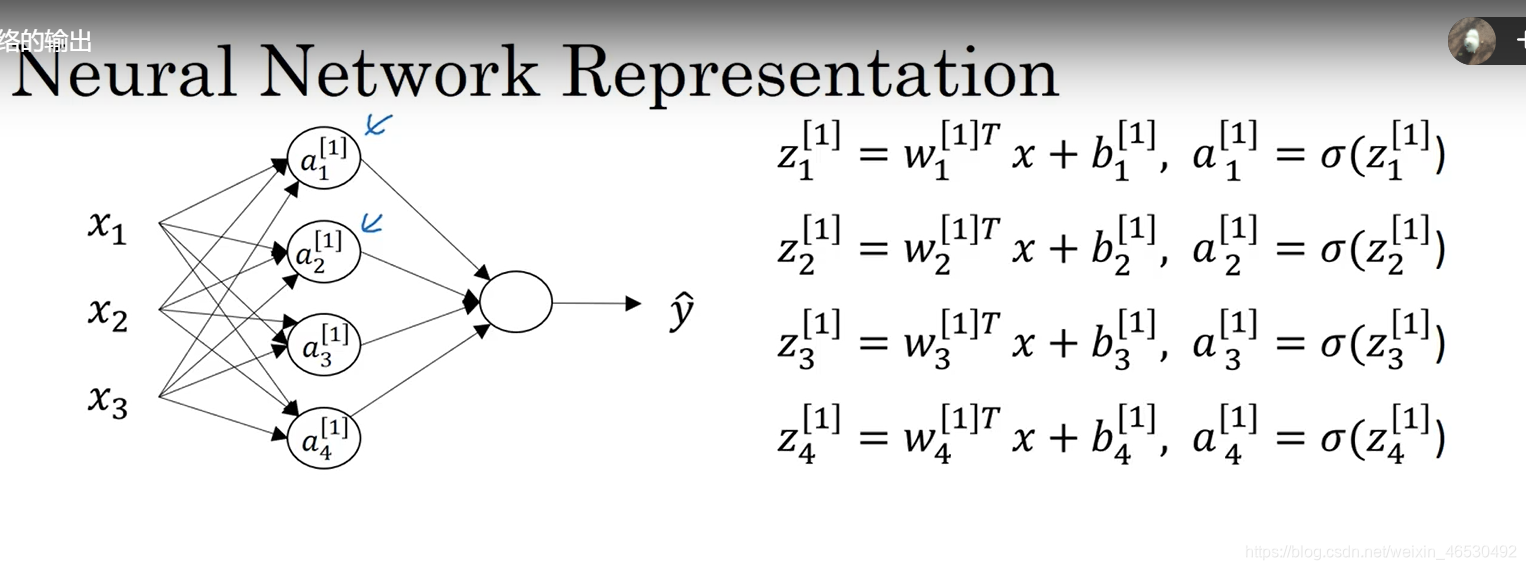
3.4 多个样本的向量化
3.5 向量化实现的解释
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ycUwobxo-1625930799961)(../AppData/Roaming/Typora/typora-user-images/image-20210709225154841.png)]](https://img-blog.csdnimg.cn/20210710233906149.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NjUzMDQ5Mg==,size_16,color_FFFFFF,t_70)
3.6激活函数
tanh激活函数几乎总比sigma函数表现更好,使得数据的平均值接近0,有标准化的效果。
但是输出层要求值为0或1,所以输出层建议用sigma函数。
选择激活函数的经验法则
sigma函数:二元分类,输出值要求是0或者1(输出层)
ReLU函数:其他单元都用
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i3C8Xbi5-1625930799962)(../AppData/Roaming/Typora/typora-user-images/image-20210709230639393.png)]](https://img-blog.csdnimg.cn/20210710233936997.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NjUzMDQ5Mg==,size_16,color_FFFFFF,t_70)
3.7 为什么需要激活函数?
可以理解成激活函数实际上是把输出值控制在一定的范围内。
3.8 激活函数的导数
sigma函数
g
(
z
)
=
σ
(
z
)
=
1
1
+
e
?
z
a
=
g
(
z
)
g
′
(
z
)
=
1
1
+
e
?
z
(
1
?
1
1
+
e
?
z
)
=
a
(
1
?
a
)
g(z) = \sigma(z) = \frac{1}{1+e^{-z}}\\ a = g(z)\\ g'(z) = \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=a(1-a)\\
g(z)=σ(z)=1+e?z1?a=g(z)g′(z)=1+e?z1?(1?1+e?z1?)=a(1?a)
tanh函数
g
(
z
)
=
t
a
n
h
(
z
)
=
e
x
?
e
?
x
e
x
+
e
?
x
g
′
(
z
)
=
1
?
(
e
x
?
e
?
x
e
x
+
e
?
x
)
2
=
1
?
a
2
g(z) = tanh(z) = \frac{e^x-e^{-x}}{e^x+e^{-x}}\\ g'(z) = 1-( \frac{e^x-e^{-x}}{e^x+e^{-x}})^2 = 1-a^2\\
g(z)=tanh(z)=ex+e?xex?e?x?g′(z)=1?(ex+e?xex?e?x?)2=1?a2
ReLU函数
KaTeX parse error: Undefined control sequence: \mbox at position 60: …rray}{rcl} 0 & \?m?b?o?x?{for} & z<0 \\ …
3.9 神经网络的梯度下降法
3.10 直观理解反向传播
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ObeON5ay-1625930799963)(../AppData/Roaming/Typora/typora-user-images/image-20210710153249133.png)]](https://img-blog.csdnimg.cn/20210710234032648.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NjUzMDQ5Mg==,size_16,color_FFFFFF,t_70)
3.11 随机初始化
W初始化不能选择0,b可以
初始化选择的参数应该小一些,不然会减慢学习速度。
4.1 深层神经网络
4.2 前向和反向传播
4.3 深层网络中的前向传播
4.4 核对矩阵的维数
样本中各个量的维度
W
[
l
]
:
(
n
[
l
]
,
n
[
l
?
1
]
)
b
[
l
]
:
(
n
[
l
]
,
1
)
d
W
[
l
]
:
(
n
[
l
]
,
n
[
l
?
1
]
)
d
b
[
l
]
:
(
n
[
l
]
,
1
)
W^{[l]}:(n^{[l]},n^{[l-1]})\\ b^{[l]}:(n^{[l]},1)\\ dW^{[l]}:(n^{[l]},n^{[l-1]})\\ db^{[l]}:(n^{[l]},1)
W[l]:(n[l],n[l?1])b[l]:(n[l],1)dW[l]:(n[l],n[l?1])db[l]:(n[l],1)
z [ 0 ] = w [ 0 ] x + b [ 0 ] ( n [ 1 ] , 1 ) ( n [ 1 ] , n [ 0 ] ) ( n [ 0 ] , 1 ) ( n [ 1 ] , 1 ) Z [ 0 ] = W [ 0 ] X + b ( n [ 1 ] , m ) ( n [ 1 ] , n [ 0 ] ) ( n [ 0 ] , m ) ( n [ 1 ] , m ) d Z [ l ] , d A [ l ] : ( n [ l ] , m ) z^{[0]} = \quad w^{[0]}\quad \quad x\quad+b^{[0]}\\ (n^{[1]},1) (n^{[1]},n^{[0]})(n^{[0]},1) (n^{[1]},1)\\ Z^{[0]} = \quad W^{[0]}\quad X+\quad b\\ (n^{[1]},m) (n^{[1]},n^{[0]})(n^{[0]},m) (n^{[1]},m)\\ dZ^{[l]},dA^{[l]}:(n^{[l]},m) z[0]=w[0]x+b[0](n[1],1)(n[1],n[0])(n[0],1)(n[1],1)Z[0]=W[0]X+b(n[1],m)(n[1],n[0])(n[0],m)(n[1],m)dZ[l],dA[l]:(n[l],m)
4.5 为什么使用深层表示
4.6 搭建深层网络神经块
4.7 参数VS超参数
W、b:参数
影响W、b的参数叫做超参数