[人工智能]吴恩达机器学习笔记（十五）——推荐系统

1.问题规划

推荐系统在我们的日常生活中其实很常见，比如电影推荐等等。因此下面就以电影推荐为例子介绍推荐系统。

首先如下图所示：

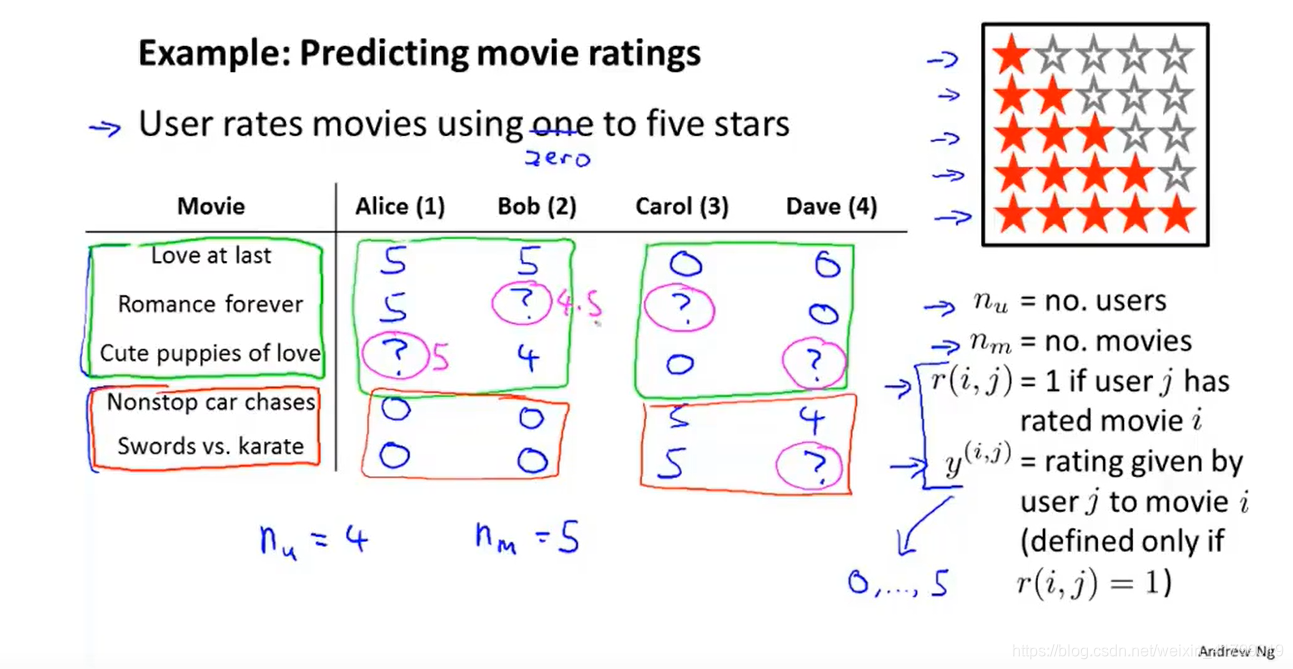
上图中的一些信息点包括如下：

1. 例子是一个电影评分的例子，用户可以对电影进行0~5的评分。如果用户未对某个电影进行评分，那么就会被标记为？。
2. 从图中可以看到，Alice和Bob对于前三个电影的评分较高，这三个电影大多偏向于爱情。而对于后面两个电影的评分则为0，这两个电影偏向于动作类。Carol和Dave则与之相反。
3. 定义几个符号：n_u代表用户的数量，这里n_u=4。n_m代表电影的数量，这里n_m=5。r(i,j)代表电影i是否被用户j评价过，若r(i,j)=1则表示评价过。y^(i,j)代表用户j对于电影i的评分（前提是r*(i,j)=1）。
4. 我们的推荐系统就可以去尝试预测？的值，从而将评分高的推荐给用户。

2.基于内容的推荐算法

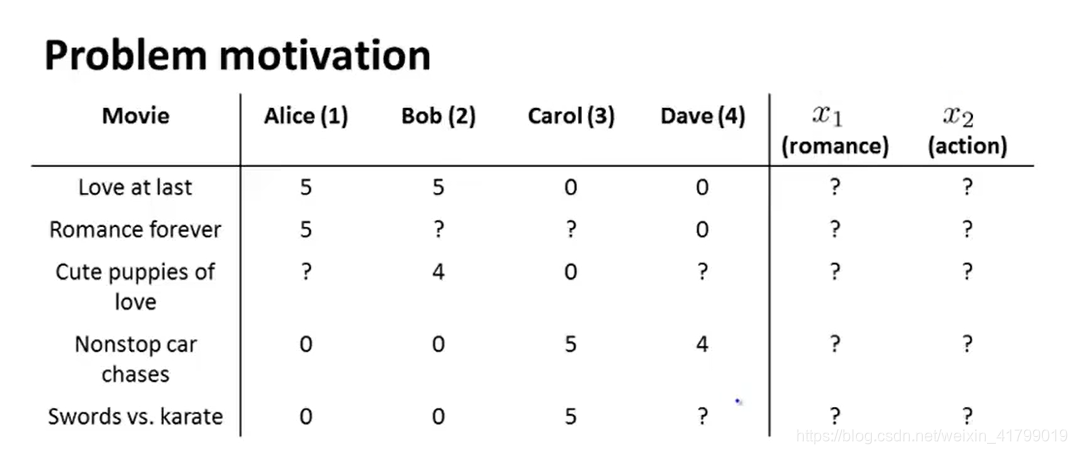
现在假设每部电影拥有两个特征，romance和action，基于此可以构建每个电影的特征向量，如下图所示：

我们可以看成一个线性回归的问题。
对于每一个用户j，学习参数θ^(j)∈R³。从而通过(θ^(j))^Tx⁽ⁱ⁾来获得用户j对于电影i的评价。
例如下图展示了第一个用户对于第三个电影的评分预测方式：

下面整理一下上面的符号：

1. r(i,j)代表电影i是否被用户j评价过，若r(i,j)=1则表示评价过
2. y^(i,j)代表用户j对于电影i的评分（前提是r*(i,j)=1）
3. θ^(j)代表用户j的参数向量
4. x⁽ⁱ⁾代表电影i的特征向量
5. 用户j对于电影i评分的预测值为(θ^(j))^Tx⁽ⁱ⁾
6. m^(j)代表用户j评价电影的数量

因此，为了得到参数θ^(j)，我们需要最小化下面这个式子：

为了简化这个公式，我们可以将m^(j)省略掉，这并不会影响我们取得最优值，得到如下公式：

进一步，我们如果要学习所有用户的参数，可以得到下列式子：

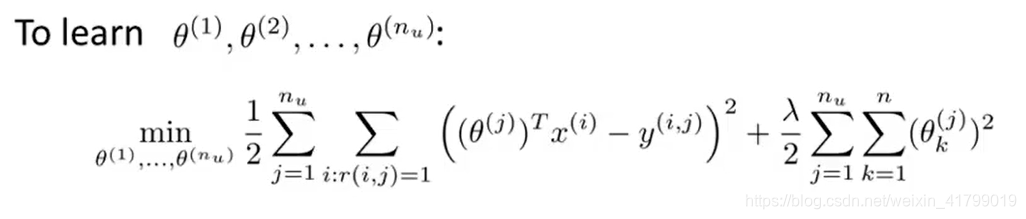
进一步，我们可以对代价函数进行梯度下降，得到如下式子：

3.协同过滤

下面介绍协同过滤算法来构建推荐系统， 这种算法可以自行学习所要使用的特征。
当我们无法像上一小节一样获得电影的romance和action时，如下图所示：

但是我们拥有了每个用户喜欢romance和action的程度，并建立了如下向量：

基于用户的这些喜好特征θ^(j)，我们就可以计算出电影的特征，如下所示：

同样地，我们为了获得电影的特征，需要最小化以下表达式：

进一步，我们要获得全部电影的特征，我们需要最小化以下表达式：

最后，我们对基于内容的推荐和基于电影特征的推荐进行以下总结，如下图所示：

通过θ，我们可以求出x。通过x，我们可以求出θ。
这就有点鸡生蛋，蛋生鸡的意思了。
因此，我们能够想到的是，可以随机初始化一个θ，然后生成x。再用生成的x，去生成更优的θ，不断进行迭代下去，得到最优的θ和x。

这其实就是协同过滤算法的思想了。
因为每一个用户都对一部分电影进行了评价，也就是每个用户都对推荐系统做出了贡献。然后通过这些贡献，我们又可以去预测其他用户的评分。协同的另一层意思就是每个用户都在帮助进行更好地特征学习。

4.协同过滤算法

上一小节中讲到可以通过不断迭代计算下面两个式子从而得到最优的θ和x：

但是实际上有更好的方法可以避免这个不断迭代的过程，使得计算更加高效。
将上面两个代价函数进行结合，可以得到下面的代价函数，可以同时最小化x和θ。如下图所示：

注意：当我们使用上面这个式子进行学习的时候，就不需要额外设置x₀=1。也就是x∈Rⁿ，θ∈Rⁿ。这是和前面讲的迭代方式的不同。

下面总结一下协同过滤算法的流程：

1. 随机初始化参数θ和x
   

2. 使用梯度下降优化代价函数，求得最优的θ和x。因为x∈Rⁿ，θ∈Rⁿ，所以正则项不用单独考虑。
   

3. 给一个用户的θ，可以通过学习到的x，计算θ^Tx来得到用户对于电影的评分。

5.矢量化：低秩矩阵分解

下面介绍我们如何使用我们刚刚介绍的算法进行向量化
首先是先对我们以后的数据进行向量化，得到下图：

对于预测矩阵，我们可以通过Xθ^T来进行计算，如下图所示：

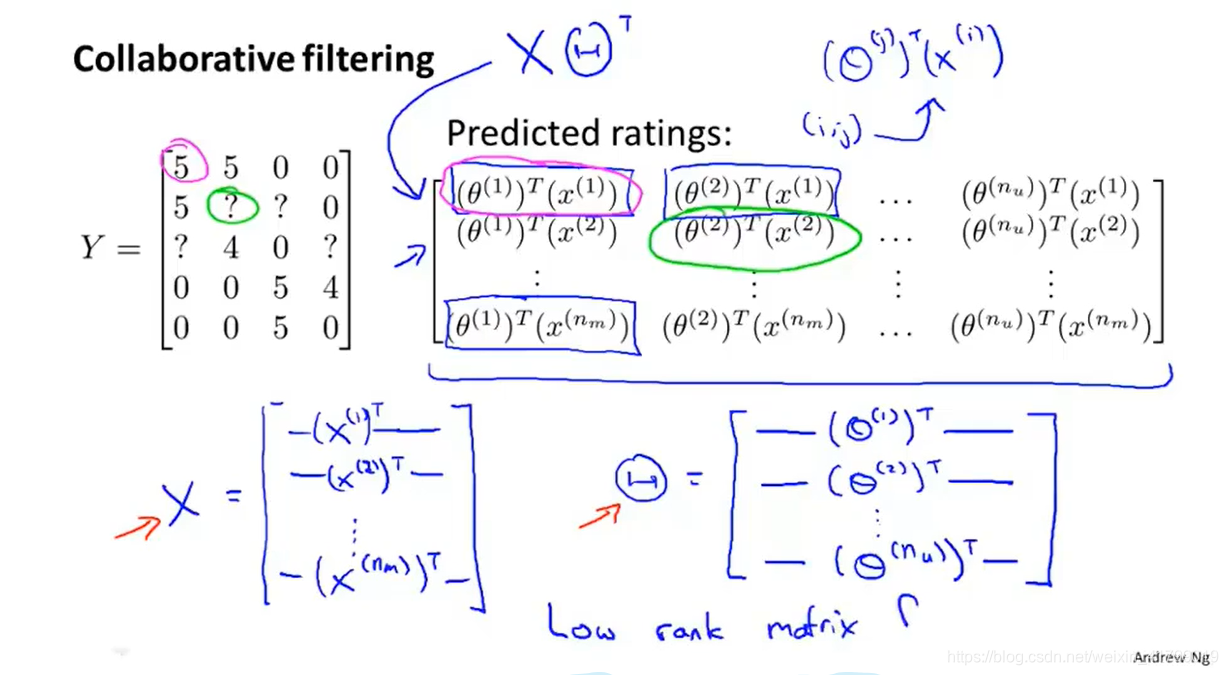
这个协同过滤算法也有另外一个名字叫做低秩矩阵分解。

最后，当我们使用算法找到了我们想要的θ和x。我们要来如何找到相似的电影呢。
假设我们已经通过协同过滤算法得到了电影的特征x，如下：

我们可以通过计算两个电影的特征x之间的距离来找到相似的电影，如下所示：

6.实施细节：均值规范化

现在假设多了一个用户5叫做Eve，他没有对任何电影做过评价，如下所示：

对于我们要优化的代价函数

因为Eve没有做过评价，所以不会影响代价函数的第一项。唯一会有影响的是最后一项。因为我们是希望目标函数尽可能小，那么我们就会得到θ⁽⁵⁾是一个零向量。
紧接着，使用Eve的θ⁽⁵⁾给电影打分，θ⁽⁵⁾x=0。这样就导致所有打分为0，就会影响整体的数据，并且也没办法推荐电影给他。

均值归一化的思想就可以解决这个问题。
首先，我们将Eve的评分也添加到矩阵中，并计算每个电影评分的均值，如下图所示：

然后让每一个评分减去均值，使得电影评分的均分为0：

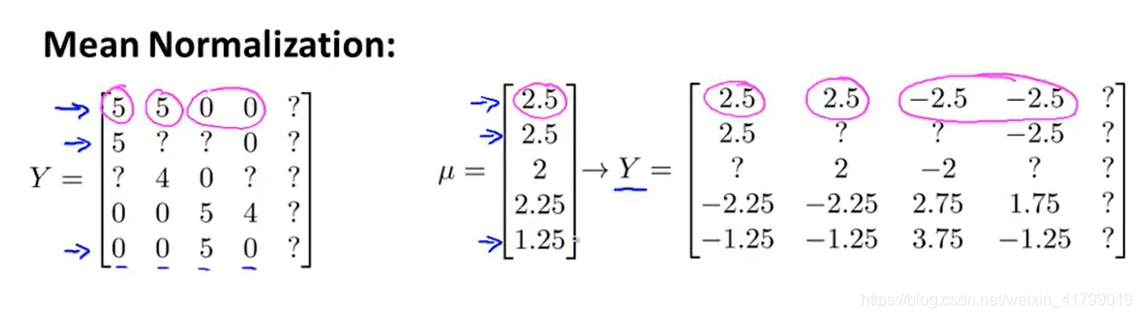
接着使用新的矩阵Y进行协同过滤算法去学习参数θ和x。
最后，当我们进行预测的时候就需要加回我们刚刚计算的均值，如下图所示。

通过这样我们就可以使得Eve的评价不会是一个零向量，如下所示：